Clustering k-means in python: esempio passo passo

Uno degli algoritmi di clustering più comuni nell’apprendimento automatico è noto come clustering k-means .

Il clustering K-means è una tecnica in cui inseriamo ciascuna osservazione da un set di dati in uno dei cluster K.

L’obiettivo finale è quello di avere K cluster in cui le osservazioni all’interno di ciascun cluster sono abbastanza simili tra loro mentre le osservazioni nei diversi cluster sono abbastanza diverse l’una dall’altra.

In pratica, utilizziamo i seguenti passaggi per eseguire il clustering K-means:

1. Scegli un valore per K.

• Innanzitutto, dobbiamo decidere quanti cluster vogliamo identificare nei dati. Spesso dobbiamo semplicemente testare diversi valori diversi per K e analizzare i risultati per vedere quale numero di cluster sembra avere più senso per un dato problema.

2. Assegnare casualmente ciascuna osservazione a un cluster iniziale, da 1 a K.

3. Eseguire la seguente procedura finché le assegnazioni dei cluster non smettono di cambiare.

• Per ciascuno dei K cluster, calcola il centro di gravità del cluster. Questo è semplicemente il vettore delle caratteristiche p- medie per le osservazioni del cluster k-esimo .
• Assegna ciascuna osservazione al cluster con il baricentro più vicino. Qui, il più vicino è definito utilizzando la distanza euclidea .

Il seguente esempio passo passo mostra come eseguire il clustering k-means in Python utilizzando la funzione KMeans dal modulo sklearn .

Passaggio 1: importa i moduli necessari

Per prima cosa importeremo tutti i moduli di cui avremo bisogno per eseguire il clustering k-means:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Passaggio 2: crea il DataFrame

Successivamente, creeremo un DataFrame contenente le seguenti tre variabili per 20 diversi giocatori di basket:

• punti
• aiuto
• rimbalza

Il codice seguente mostra come creare questo DataFrame panda:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

Utilizzeremo il clustering k-means per raggruppare attori simili in base a questi tre parametri.

Passaggio 3: pulire e preparare DataFrame

Quindi eseguiremo i seguenti passaggi:

• Usa dropna() per eliminare righe con valori NaN in qualsiasi colonna
• Utilizza StandardScaler() per ridimensionare ciascuna variabile in modo che abbia una media pari a 0 e una deviazione standard pari a 1.

Il codice seguente mostra come eseguire questa operazione:

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

Nota : utilizziamo il ridimensionamento in modo che ciascuna variabile abbia la stessa importanza quando si adatta l’algoritmo k-medie. Altrimenti le variabili con gli intervalli più ampi avrebbero troppa influenza.

Passaggio 4: trovare il numero ottimale di cluster

Per eseguire il clustering k-means in Python, possiamo usare la funzione KMeans dal modulo sklearn .

Questa funzione utilizza la seguente sintassi di base:

KMeans(init=’random’, n_clusters=8, n_init=10, random_state=Nessuno)

Oro:

• init : controlla la tecnica di inizializzazione.
• n_clusters : il numero di cluster in cui posizionare le osservazioni.
• n_init : il numero di inizializzazioni da eseguire. L’impostazione predefinita consiste nell’eseguire l’algoritmo k-means 10 volte e restituire quello con il SSE più basso.
• random_state : un valore intero che puoi scegliere per rendere riproducibili i risultati dell’algoritmo.

L’argomento più importante di questa funzione è n_clusters, che specifica in quanti cluster inserire le osservazioni.

Tuttavia, non sappiamo in anticipo quanti cluster siano ottimali, quindi dobbiamo creare un grafico che mostri il numero di cluster e l’SSE (somma degli errori quadrati) del modello.

In genere, quando creiamo questo tipo di trama, cerchiamo un “ginocchio” in cui la somma dei quadrati inizia a “piegarsi” o a livellarsi. Questo è generalmente il numero ottimale di cluster.

Il codice seguente mostra come creare questo tipo di grafico che visualizza il numero di cluster sull’asse x e SSE sull’asse y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

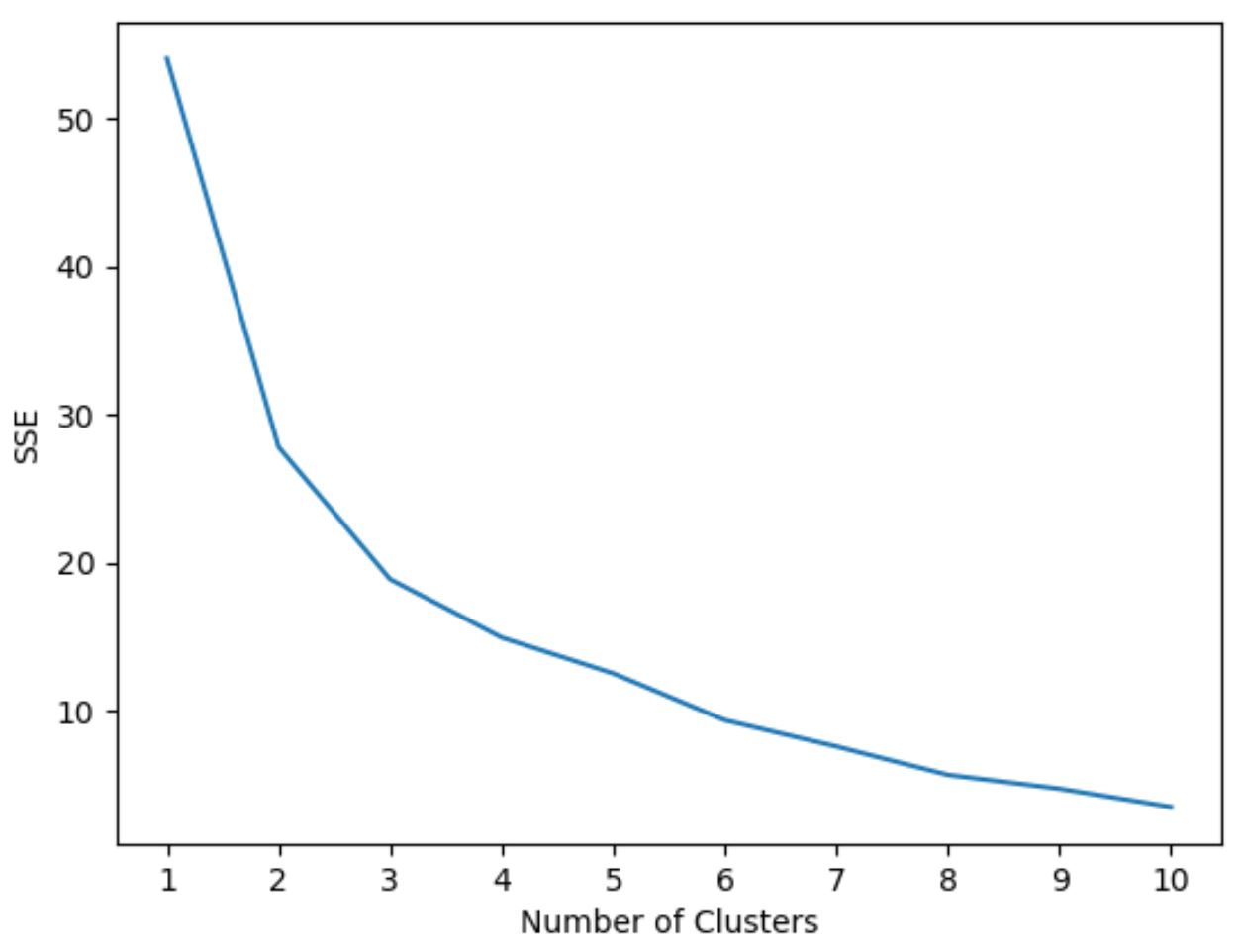
In questo grafico, sembra che ci sia un nodo o “ginocchio” in k = 3 cluster .

Pertanto, utilizzeremo 3 cluster per adattare il nostro modello di clustering k-mean nel passaggio successivo.

Nota : nel mondo reale, si consiglia di utilizzare una combinazione di queste competenze di trama e dominio per scegliere il numero di cluster da utilizzare.

Passaggio 5: eseguire il clustering K-Means con K ottimale

Il codice seguente mostra come eseguire il clustering k-means sul set di dati utilizzando il valore ottimale per k di 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

La tabella risultante mostra le assegnazioni dei cluster per ciascuna osservazione nel DataFrame.

Per rendere questi risultati più facili da interpretare, possiamo aggiungere una colonna al DataFrame che mostra l’assegnazione del cluster di ciascun giocatore:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

La colonna cluster contiene un numero di cluster (0, 1 o 2) a cui è stato assegnato ciascun giocatore.

I giocatori appartenenti allo stesso cluster hanno valori approssimativamente simili per le colonne punti , assist e rimbalzi .

Nota : puoi trovare la documentazione completa per la funzione KMeans di sklearn qui .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Python:

Come eseguire la regressione lineare in Python
Come eseguire la regressione logistica in Python
Come eseguire la convalida incrociata K-Fold in Python