Clustering delle medie k in r: esempio passo passo

Il clustering è una tecnica di apprendimento automatico che tenta di trovare gruppi di osservazioni all’interno di un set di dati.

L’obiettivo è trovare cluster tali che le osservazioni all’interno di ciascun cluster siano abbastanza simili tra loro, mentre le osservazioni in cluster diversi siano abbastanza diverse l’una dall’altra.

Il clustering è una forma di apprendimento non supervisionato perché stiamo semplicemente cercando di trovare la struttura all’interno di un set di dati invece di prevedere il valore di una variabile di risposta .

Il clustering viene spesso utilizzato nel marketing quando le aziende hanno accesso a informazioni quali:

• Reddito familiare
• Dimensione della famiglia
• Capofamiglia Professione
• Distanza dall’area urbana più vicina

Quando queste informazioni sono disponibili, il clustering può essere utilizzato per identificare famiglie simili e che potrebbero avere maggiori probabilità di acquistare determinati prodotti o di rispondere meglio a un certo tipo di pubblicità.

Una delle forme più comuni di clustering è nota come clustering k-mean .

Cos’è il clustering K-Means?

Il clustering K-means è una tecnica in cui inseriamo ciascuna osservazione da un set di dati in uno dei cluster K.

L’obiettivo finale è quello di avere K cluster in cui le osservazioni all’interno di ciascun cluster sono abbastanza simili tra loro mentre le osservazioni nei diversi cluster sono abbastanza diverse l’una dall’altra.

In pratica, utilizziamo i seguenti passaggi per eseguire il clustering K-means:

1. Scegli un valore per K.

• Innanzitutto, dobbiamo decidere quanti cluster vogliamo identificare nei dati. Spesso dobbiamo semplicemente testare diversi valori diversi per K e analizzare i risultati per vedere quale numero di cluster sembra avere più senso per un dato problema.

2. Assegnare casualmente ciascuna osservazione a un cluster iniziale, da 1 a K.

3. Eseguire la seguente procedura finché le assegnazioni dei cluster non smettono di cambiare.

• Per ciascuno dei K cluster, calcola il centro di gravità del cluster. Questo è semplicemente il vettore delle caratteristiche p- medie per le osservazioni del cluster k-esimo .
• Assegna ciascuna osservazione al cluster con il baricentro più vicino. Qui, il più vicino è definito utilizzando la distanza euclidea .

Clustering delle medie K in R

Il tutorial seguente fornisce un esempio passo passo di come eseguire il clustering k-means in R.

Passaggio 1: caricare i pacchetti necessari

Innanzitutto, caricheremo due pacchetti contenenti diverse funzioni utili per il clustering k-means in R.

 library (factoextra)
library (cluster)

Passaggio 2: caricare e preparare i dati

Per questo esempio, utilizzeremo il set di dati USArrests integrato in R, che contiene il numero di arresti ogni 100.000 persone in ciascuno stato degli Stati Uniti nel 1973 per omicidio , aggressione e stupro , nonché la percentuale della popolazione di ciascuno stato che vive in aree urbane le zone. , UrbanPop .

Il codice seguente mostra come eseguire le seguenti operazioni:

• Carica il set di dati sugli arresti USA
• Rimuovi tutte le righe con valori mancanti
• Scalare ciascuna variabile nel set di dati in modo che abbia una media pari a 0 e una deviazione standard pari a 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Passaggio 3: trovare il numero ottimale di cluster

Per eseguire il clustering k-means in R, possiamo utilizzare la funzione kmeans() integrata, che utilizza la seguente sintassi:

kmeans (dati, centri, nstart)

Oro:

• dati: nome del set di dati.
• centri: il numero di cluster, indicato con k .
• nstart: il numero di configurazioni iniziali. Poiché è possibile che diversi cluster iniziali portino a risultati diversi, si consiglia di utilizzare diverse configurazioni iniziali. L’algoritmo k-means troverà le configurazioni iniziali che portano alla variazione più piccola all’interno del cluster.

Poiché non sappiamo in anticipo quanti cluster sono ottimali, creeremo due diversi grafici che possono aiutarci a decidere:

1. Numero di cluster rispetto al totale nella somma dei quadrati

Innanzitutto, utilizzeremo la funzione fviz_nbclust() per creare un grafico del numero di cluster rispetto al totale nella somma dei quadrati:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

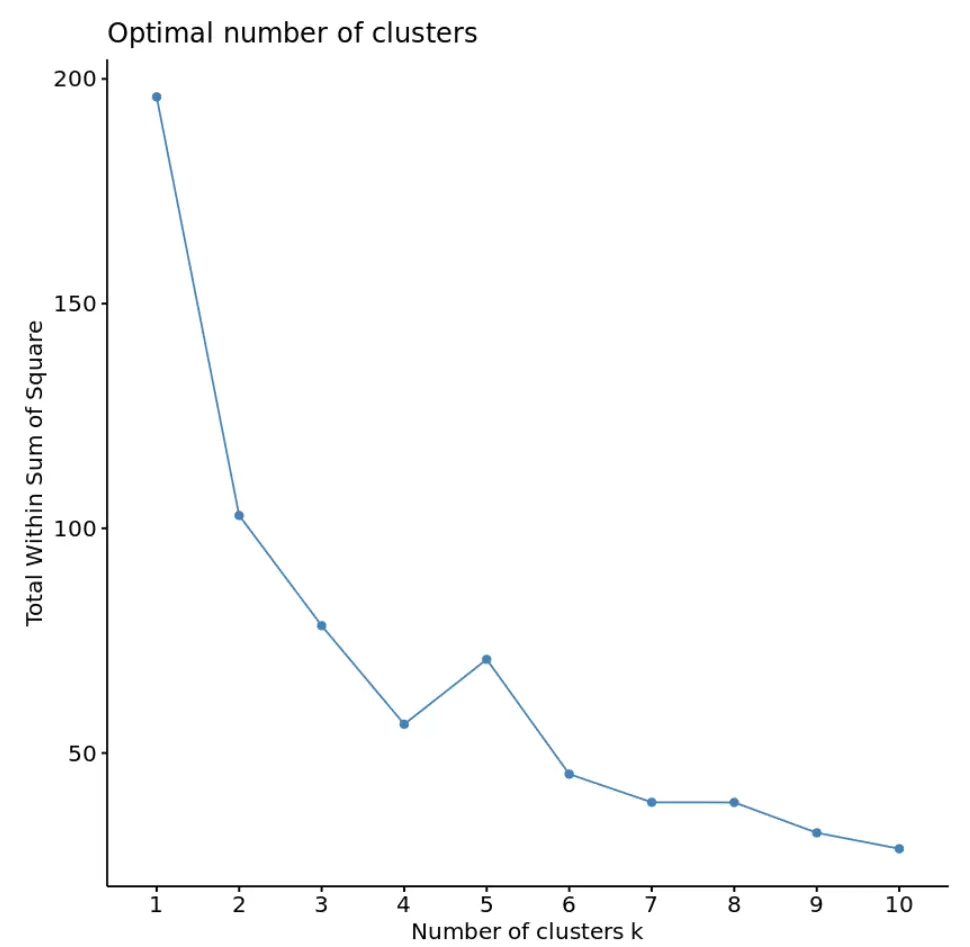
In genere, quando creiamo questo tipo di trama, cerchiamo un “ginocchio” in cui la somma dei quadrati inizia a “piegarsi” o a livellarsi. Questo è generalmente il numero ottimale di cluster.

Per questo grafico, sembra che ci sia una piccola piega o “piegatura” in k = 4 cluster.

2. Numero di cluster rispetto alle statistiche del gap

Un altro modo per determinare il numero ottimale di cluster è utilizzare una metrica chiamata statistica di deviazione , che confronta la variazione totale intra-cluster per diversi valori di k con i loro valori attesi per una distribuzione senza clustering.

Possiamo calcolare la statistica del gap per ciascun numero di cluster utilizzando la funzione clusGap() dal pacchetto cluster e tracciare i cluster rispetto alle statistiche del gap utilizzando la funzione fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

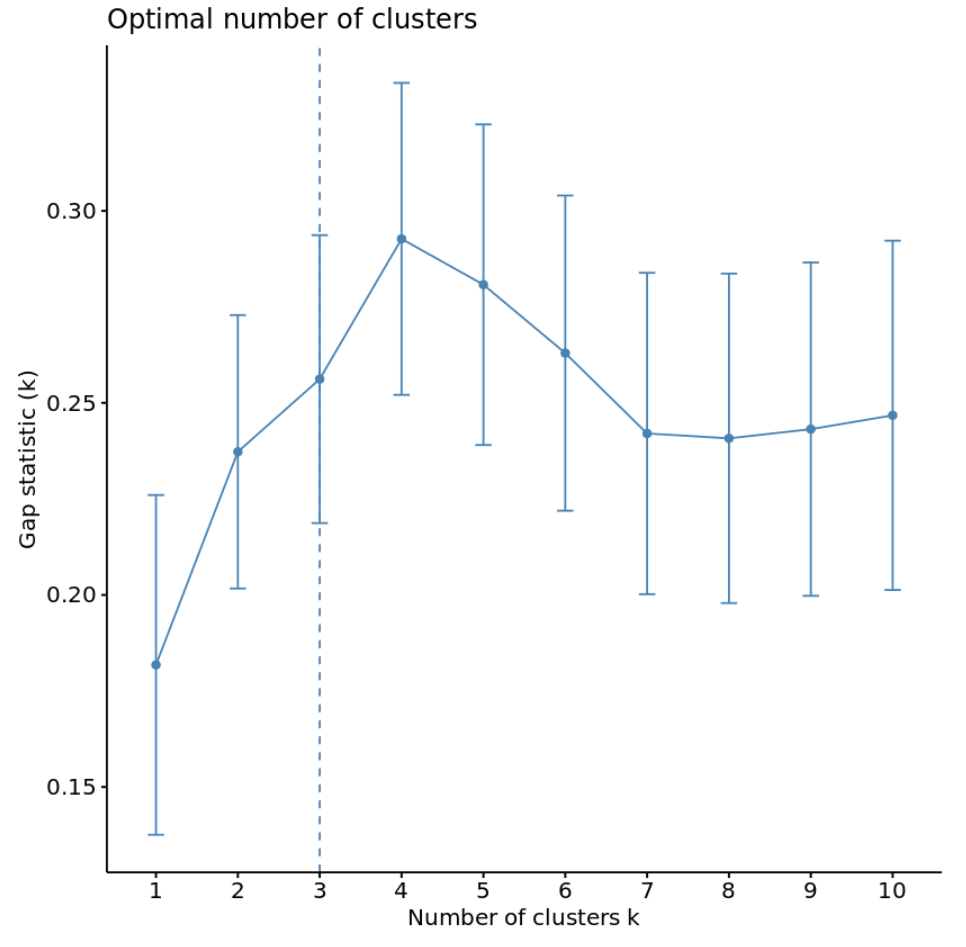
Dal grafico possiamo vedere che la statistica del gap è massima con k = 4 cluster, che corrisponde al metodo del gomito utilizzato in precedenza.

Passaggio 4: eseguire il clustering K-Means con K ottimale

Infine, possiamo eseguire il clustering k-means sul set di dati utilizzando il valore ottimale per k di 4:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Dai risultati possiamo vedere che:

• 16 stati sono stati assegnati al primo cluster
• 13 stati sono stati assegnati al secondo cluster
• 13 stati sono stati assegnati al terzo cluster
• 8 stati sono stati assegnati al quarto cluster

Possiamo visualizzare i cluster su un grafico a dispersione che mostra le prime due componenti principali sugli assi utilizzando la funzione fivz_cluster() :

 #plot results of final k-means model
fviz_cluster(km, data = df)

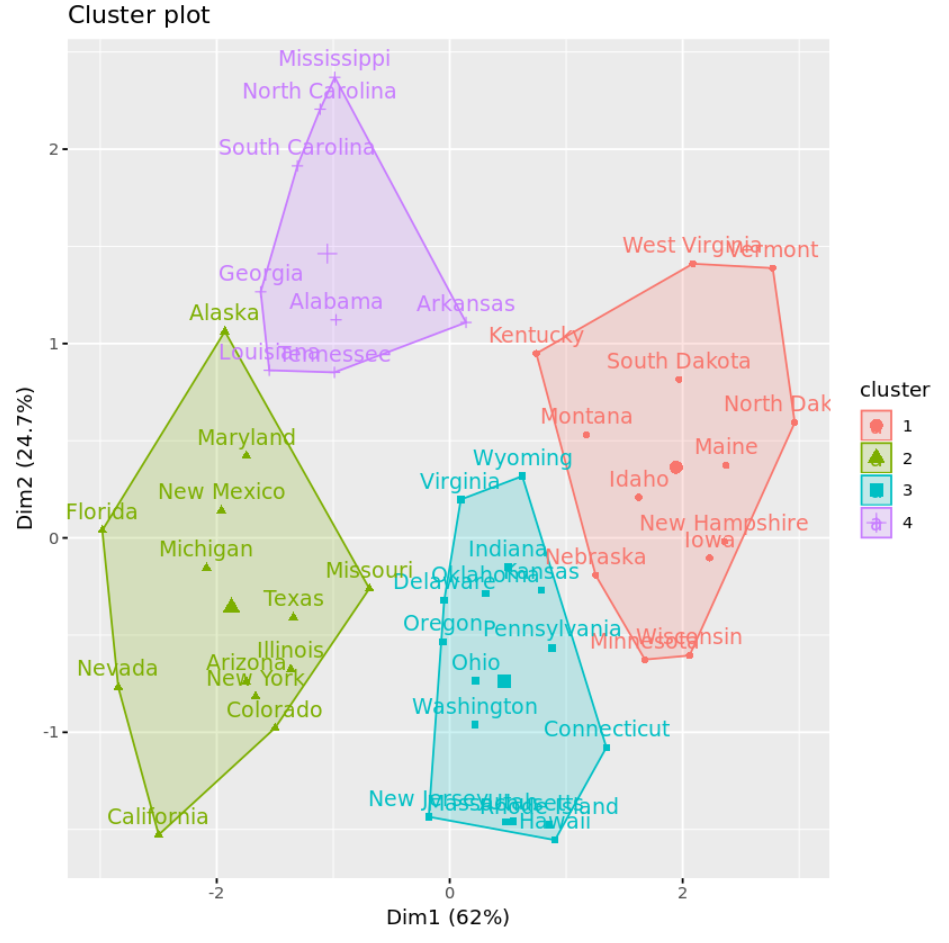
Possiamo anche utilizzare la funzione Aggregate() per trovare la media delle variabili in ciascun cluster:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

Interpretiamo questo output come segue:

• Il numero medio di omicidi ogni 100.000 cittadini negli stati del Gruppo 1 è 3,6 .
• Il numero medio di aggressioni ogni 100.000 cittadini negli stati del Gruppo 1 è 78,5 .
• La percentuale media di residenti che vivono in un’area urbana tra gli stati del Gruppo 1 è del 52,1% .
• Il numero medio di stupri ogni 100.000 cittadini negli stati del Gruppo 1 è 12,2 .

E così via.

Possiamo anche aggiungere le assegnazioni dei cluster di ciascuno stato al set di dati originale:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Vantaggi e svantaggi del clustering K-Means

Il clustering K-means offre i seguenti vantaggi:

• È un algoritmo veloce.
• Può gestire bene set di dati di grandi dimensioni.

Tuttavia, presenta i seguenti potenziali svantaggi:

• Ciò richiede di specificare il numero di cluster prima di eseguire l’algoritmo.
• È sensibile ai valori anomali.

Due alternative al clustering k-mean sono il clustering k-mean e il clustering gerarchico.

Puoi trovare il codice R completo utilizzato in questo esempio qui .