Come eseguire un test di kruskal-wallis in spss
Un test di Kruskal-Wallis viene utilizzato per determinare se esiste o meno una differenza statisticamente significativa tra le mediane di tre o più gruppi indipendenti. È considerato l’equivalente non parametrico dell’ANOVA unidirezionale .
Questo tutorial spiega come eseguire un test Kruskal-Wallis in SPSS.
Esempio: test di Kruskal-Wallis in SPSS
Un ricercatore vuole sapere se tre farmaci hanno effetti diversi sul dolore al ginocchio. Quindi recluta 30 persone che soffrono tutte di dolore al ginocchio simile e le divide casualmente in tre gruppi per ricevere il farmaco 1, il farmaco 2 o il farmaco 3.
Dopo un mese di assunzione del farmaco, il ricercatore chiede a ciascun individuo di valutare il proprio dolore al ginocchio su una scala da 1 a 100, dove 100 indica il dolore più grave. I punteggi delle 30 persone sono presentati di seguito:
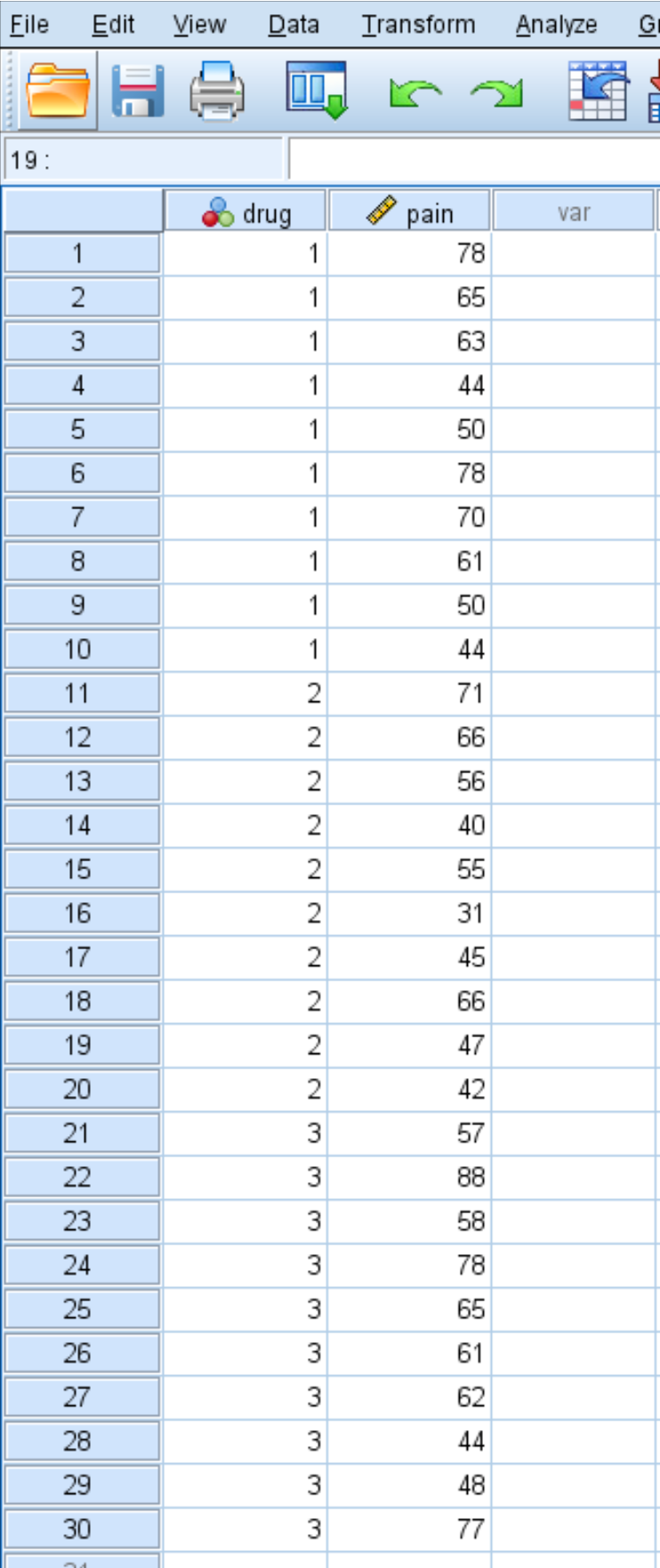
Seguire i seguenti passaggi per eseguire un test Kruskal-Wallis per determinare se esiste o meno una differenza nei livelli di dolore al ginocchio riportati tra i tre gruppi:
Passaggio 1: eseguire un test Kruskal-Wallis.
Fare clic sulla scheda Analizza , quindi su Test non parametrici , quindi su Finestre di dialogo legacy , quindi su K Campioni indipendenti :
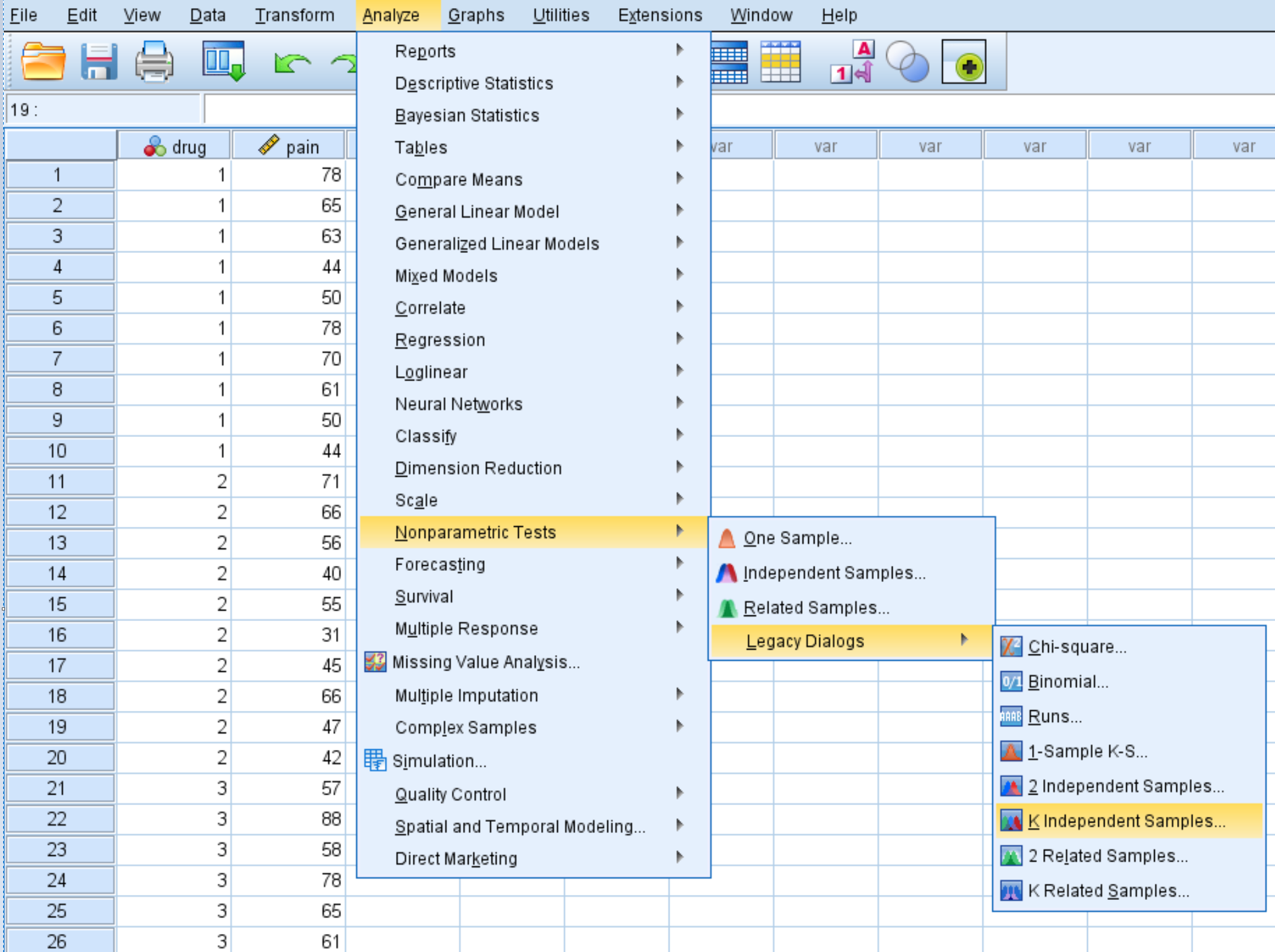
Nella finestra visualizzata, trascina la variabile del dolore nella casella denominata Elenco variabili del test e il farmaco nella casella denominata Variabile di raggruppamento. Quindi fare clic su Imposta intervallo e impostare il valore minimo su 1 e il valore massimo su 3. Quindi fare clic su Continua . Assicurati che la casella accanto a Kruskal-Wallis H sia selezionata, quindi fai clic su OK .
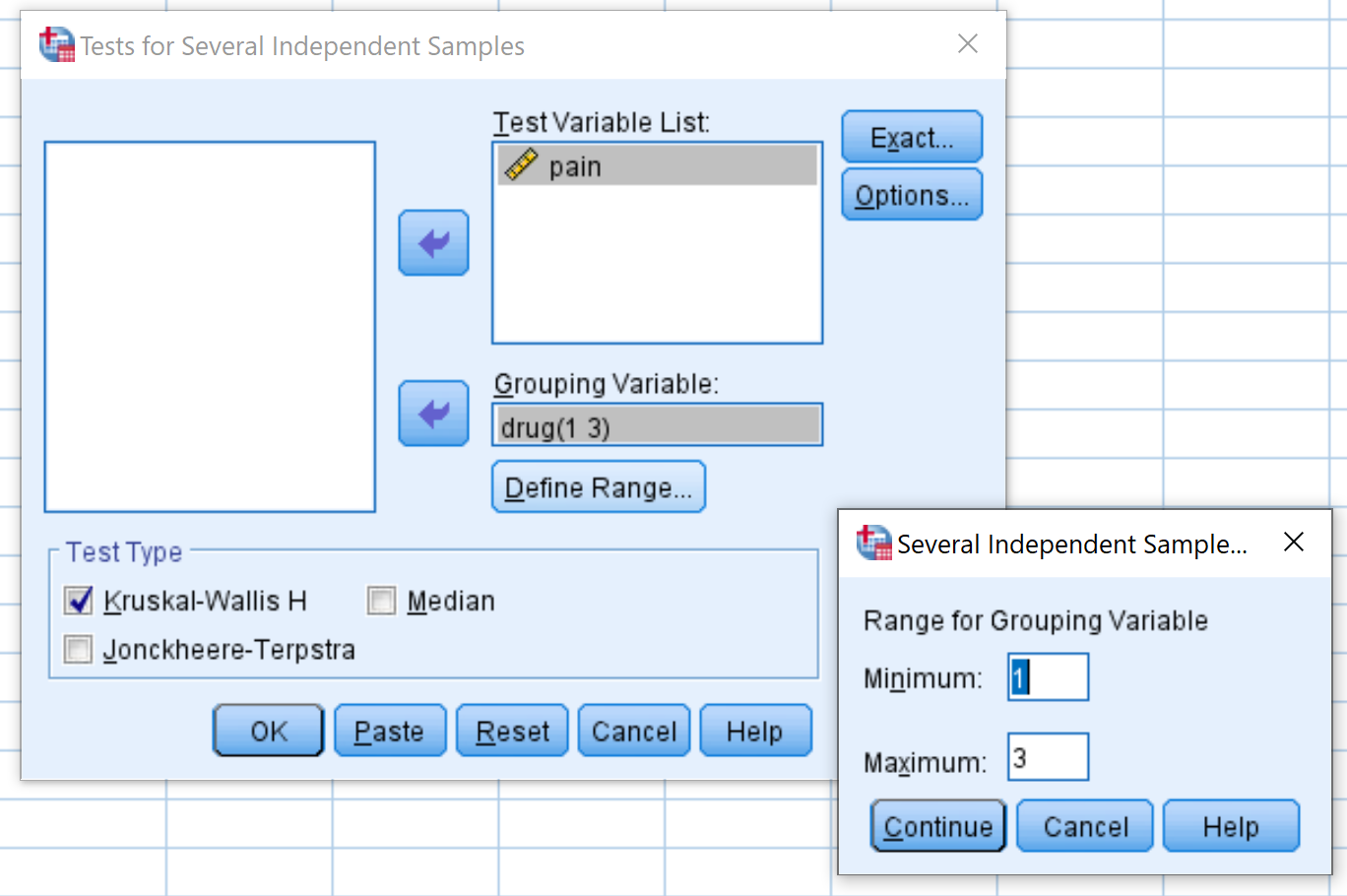
Passaggio 2: interpretare i risultati.
Dopo aver fatto clic su OK , verranno visualizzati i risultati del test Kruskal-Wallis:
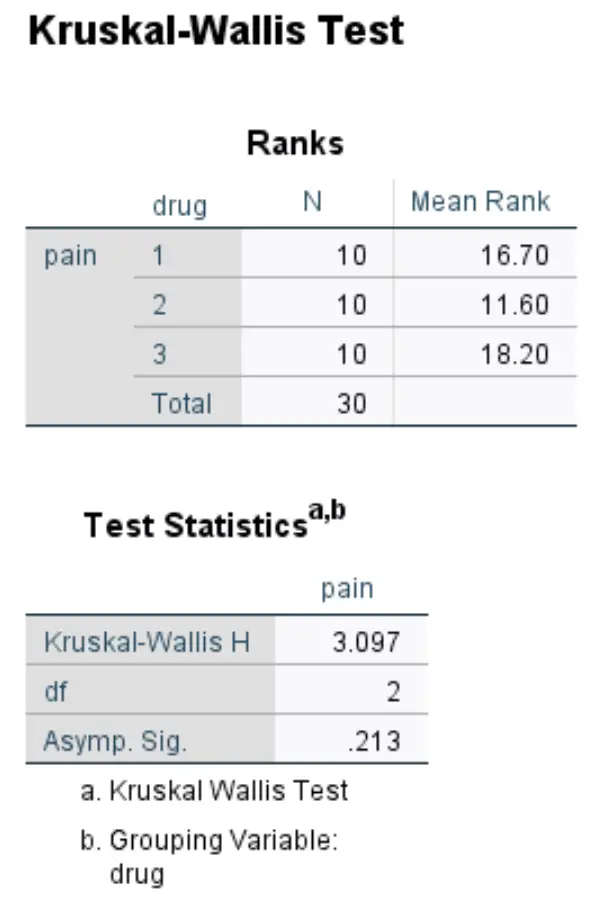
La seconda tabella nell’output mostra i risultati del test:
- Kruskal-Wallis H: Questa è la statistica del test X 2 .
- df: Questi sono i gradi di libertà, calcolati come #gruppi-1 = 3-1 = 2.
- Asintomo. Sig: questo è il valore p associato a una statistica del test X 2 di 3,097 con 2 gradi di libertà. Questo può anche essere trovato utilizzando il calcolatore del punteggio chi quadrato rispetto al valore P.
Poiché il valore p (0,213) non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa nelle valutazioni del dolore al ginocchio tra questi tre gruppi.
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più