L'importanza della statistica nell'istruzione (con esempi)

Il campo della statistica riguarda la raccolta, l’analisi, l’interpretazione e la presentazione dei dati.

Nel contesto educativo, le statistiche sono importanti per i seguenti motivi:

Motivo 1 : le statistiche consentono agli educatori di comprendere le prestazioni degli studenti utilizzando statistiche descrittive.

Motivo 2 : le statistiche consentono agli insegnanti di individuare le tendenze nel rendimento degli studenti utilizzando la visualizzazione dei dati.

Motivo 3 : La statistica consente agli educatori di confrontare diversi metodi di insegnamento utilizzando test di ipotesi.

Nel resto di questo articolo, sviluppiamo ciascuno di questi motivi.

Motivo 1: comprendere il rendimento degli studenti utilizzando le statistiche descrittive

Le statistiche descrittive vengono utilizzate per descrivere i dati.

In un contesto educativo, un insegnante può calcolare le seguenti statistiche descrittive per gli studenti della sua classe:

• Il punteggio medio di un determinato esame.
• La deviazione standard dei punteggi di un determinato esame.
• L’intervallo di punteggi di un determinato esame.
• La percentuale di studenti che hanno superato un determinato esame.
• Il 90° percentile dei risultati di un determinato esame.

Grazie a queste misurazioni, l’insegnante può comprendere meglio i risultati degli studenti della sua classe in un determinato esame.

Può quindi decidere se cambiare il suo metodo di insegnamento se troppo pochi studenti superano l’esame o eventualmente offrire ulteriori opportunità di tutoraggio agli studenti con scarsi risultati all’esame, ecc.

Nota : questi tipi di statistiche descrittive sono utilizzati a tutti i livelli di istruzione. Ad esempio, un preside può utilizzare le statistiche descrittive per monitorare i punteggi dei test degli studenti in un’intera scuola. Un dipartimento statale dell’istruzione può anche utilizzare statistiche descrittive per monitorare i punteggi dei test per gli studenti in un intero stato.

Motivo 2: individuare le tendenze utilizzando la visualizzazione dei dati

Un altro modo comune di utilizzare le statistiche nell’istruzione è visualizzare dati come grafici a linee, istogrammi, boxplot, grafici a torta e altri grafici.

Questi tipi di grafici vengono spesso utilizzati per aiutare gli insegnanti a individuare le tendenze nel rendimento in classe e nel rendimento dei singoli studenti.

Ad esempio, supponiamo che un insegnante crei il seguente grafico a barre per visualizzare il punteggio medio dell’esame durante l’anno:

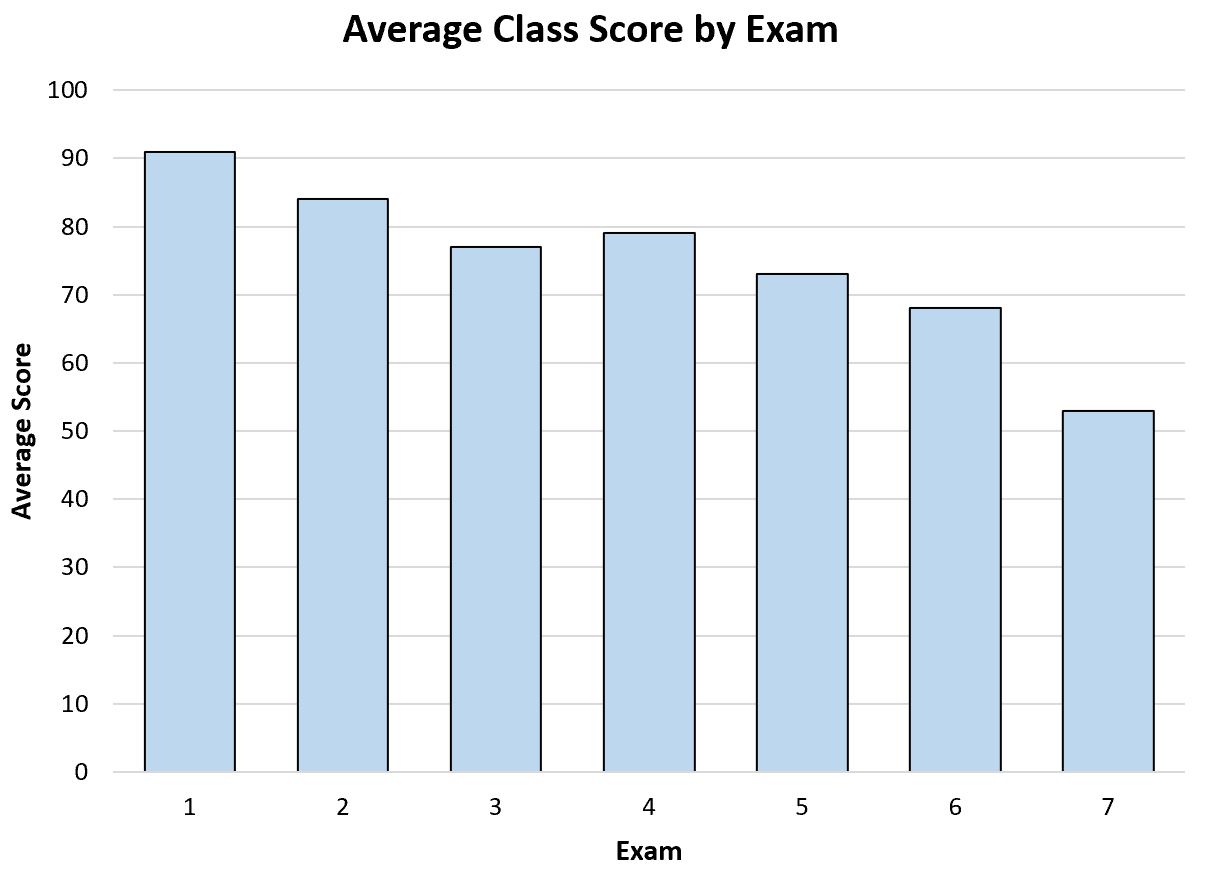
Semplicemente guardando questo grafico a barre, l’insegnante sarà in grado di vedere che il punteggio medio del test degli studenti della sua classe sta lentamente diminuendo nel corso dell’anno.

Ciò può consentire all’insegnante di migliorare i suoi metodi di insegnamento o magari di sottoporre ai suoi studenti un sondaggio per chiedere la loro opinione sui suoi metodi di insegnamento, ecc.

Motivo 3: confrontare i metodi di insegnamento utilizzando la verifica delle ipotesi

La statistica viene utilizzata anche nell’istruzione sotto forma di verifica di ipotesi .

Si tratta di test che gli educatori possono utilizzare per determinare se esiste una significatività statistica tra i diversi metodi di insegnamento.

Ad esempio, supponiamo che un insegnante voglia determinare se un determinato curriculum influisce sui punteggi dei test. Per verificarlo, seleziona casualmente 15 studenti per sostenere un pre-test. Quindi chiede a ogni studente di utilizzare il curriculum per un mese e poi un post-test di difficoltà simile.

Di seguito sono riportati i risultati dei test per ciascuno dei 15 studenti:

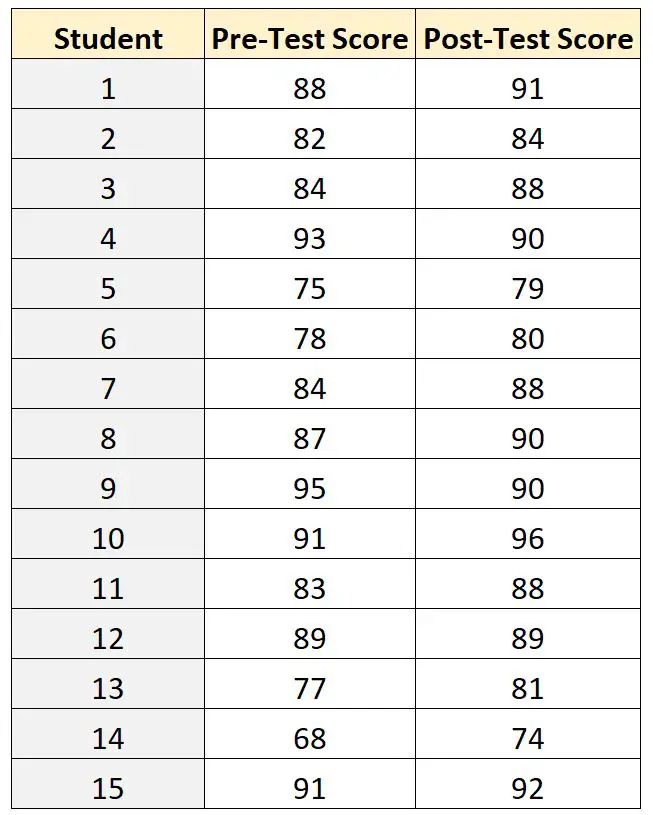
Per confrontare la differenza tra i punteggi medi pre-test e post-test, l’insegnante può utilizzare campioni di t-test accoppiati perché per ogni studente il punteggio pre-test può essere associato al punteggio post-test.

Supponiamo che il professore utilizzi un software statistico per eseguire questo t-test per campioni appaiati e riceva i seguenti risultati:

• Statistica del test t: -2,97
• valore p: 0,0101

In questo esempio, il test t per campioni accoppiati utilizza le seguenti ipotesi nulle e alternative:

• H ₀ : i punteggi medi pre-test e post-test sono uguali
• H _A : I punteggi medi pre-test e post-test non sono uguali

Poiché il valore p ( 0,0101 ) è inferiore a 0,05, rifiutiamo l’ipotesi nulla.

Ciò significa che abbiamo prove sufficienti per affermare che il punteggio medio del test è diverso per gli studenti prima e dopo la partecipazione al programma di studi.

Nota : questo è solo un esempio di verifica di ipotesi utilizzata nell’istruzione. Altri test comuni includono il t-test a un campione , il t-test a due campioni , l’ANOVA a una via e l’ANOVA a due vie .

Risorse addizionali

I seguenti articoli spiegano l’importanza delle statistiche in altri campi:

L’importanza della statistica nelle imprese
L’importanza della statistica in economia
L’importanza della statistica in sanità