La causalità implica una correlazione? (3 esempi)
È noto che la correlazione non implica causalità .
Per fare un semplice esempio, se raccogliessimo dati ogni anno sul numero totale di diplomati e sul consumo totale di pizza negli Stati Uniti, scopriremmo che le due variabili sono altamente correlate:
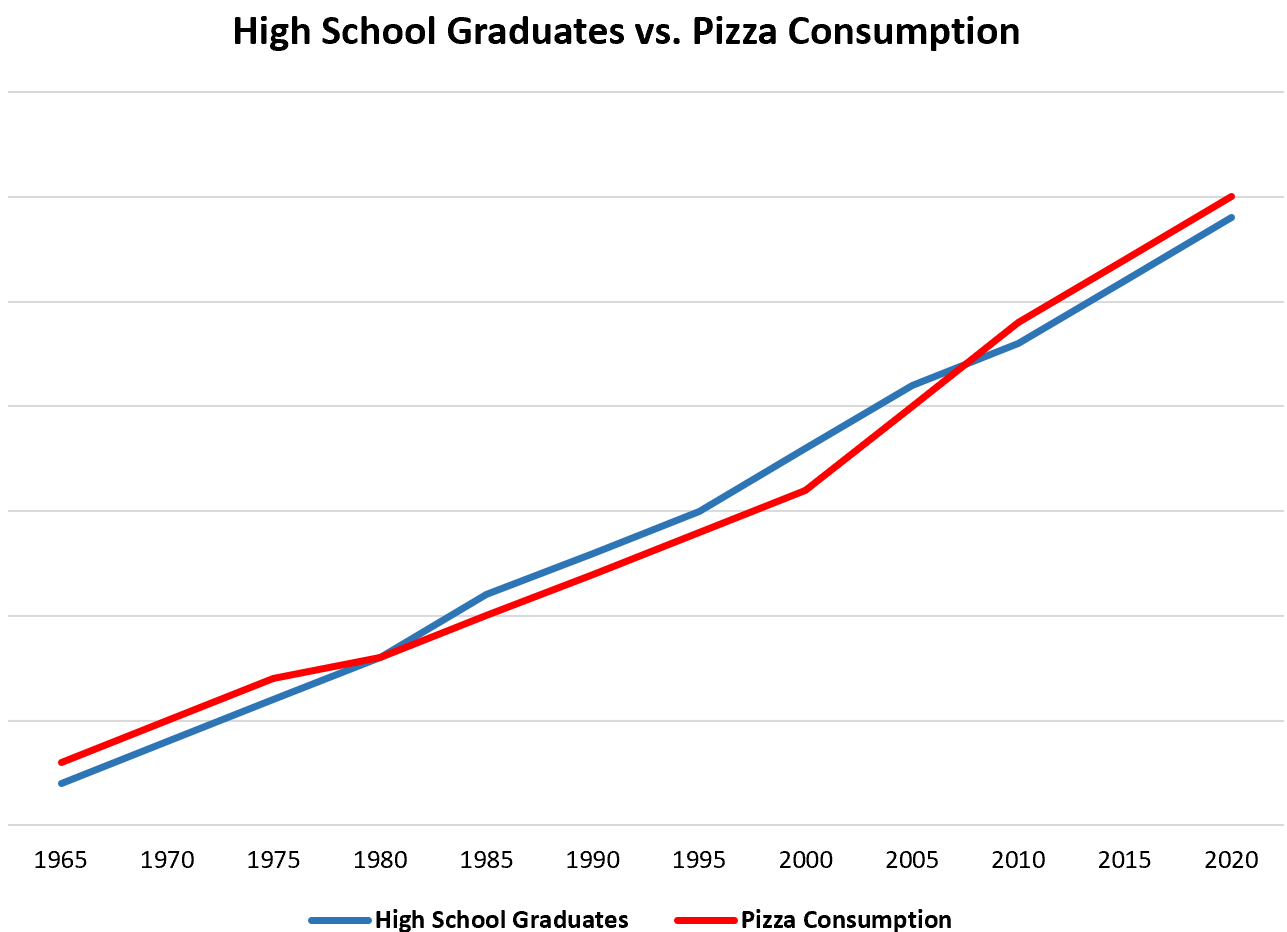
Ciò non significa che l’aumento del numero dei diplomati porti ad un aumento del consumo di pizza.
La spiegazione più probabile è che la popolazione statunitense sia aumentata nel tempo, il che significa che il numero di persone con un diploma di scuola superiore e la quantità totale di pizza consumata aumentano con l’aumento della popolazione.
Ma che dire dell’affermazione opposta: la causalità implica correlazione?
Se una variabile causa un’altra variabile, ciò significa necessariamente che le due variabili saranno correlate?
La risposta breve: no.
Gli esempi seguenti mostrano il perché.
Esempio 1: relazione quadratica
Supponiamo che una variabile, X, faccia sì che la variabile Y assuma un valore uguale a X 2 .
Per esempio:
- Se X = -10 allora Y = -10 2 = 100
- Se X = 0 allora Y = 0 2 = 0
- Se X = 10 allora Y = 10 2 = 100
E così via.
Se tracciassimo la relazione tra X e Y, sarebbe simile a questa:
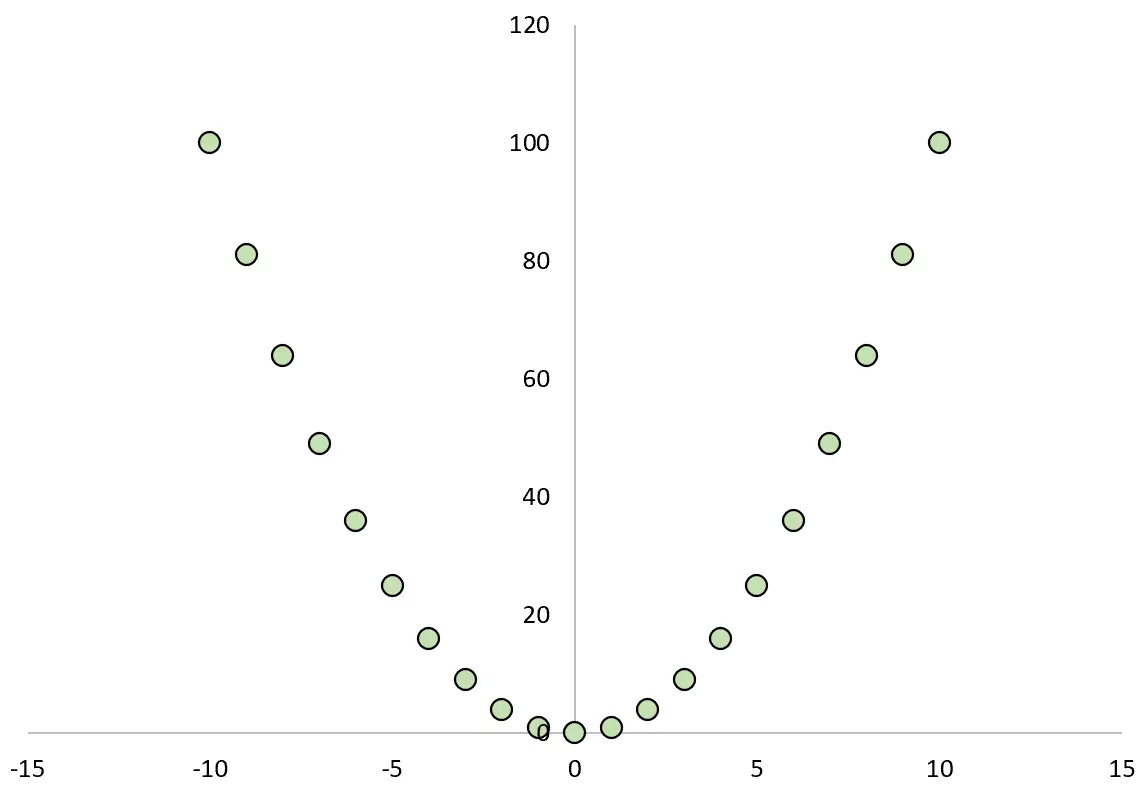
Se calcolassimo il coefficiente di correlazione di Pearson tra le due variabili, troveremmo che la correlazione è zero .
Sebbene X causi Y, la correlazione lineare tra le due variabili è zero.
Esempio 2: relazione quartica
Supponiamo che una variabile, X, faccia sì che la variabile Y assuma un valore uguale a X 4 .
Per esempio:
- Se X = -10 allora Y = -10 4 = 10.000
- Se X = 0 allora Y = 0 4 = 0
- Se X = 10 allora Y = 10 4 = 10.000
E così via.
Se tracciassimo la relazione tra X e Y, sarebbe simile a questa:
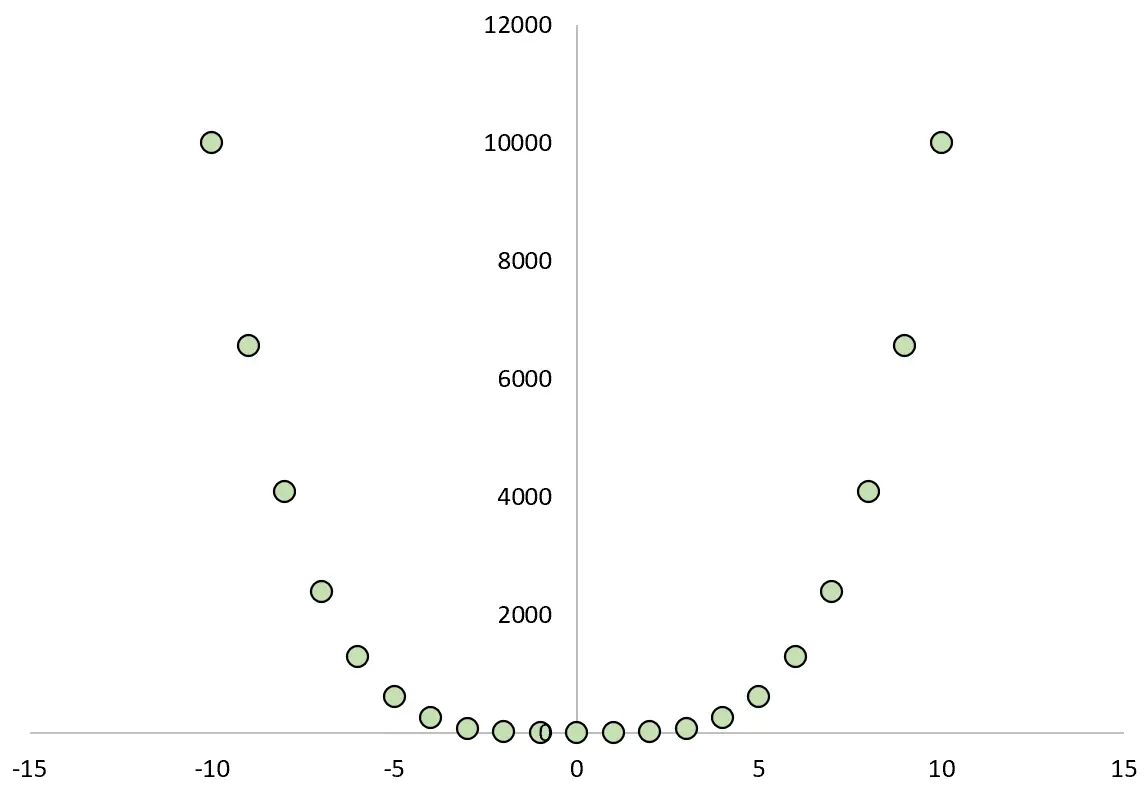
Se calcolassimo il coefficiente di correlazione di Pearson tra le due variabili, troveremmo che la correlazione è zero .
Sappiamo che X causa Y, ma la correlazione lineare tra le due variabili è zero.
Esempio 3: relazione coseno
Supponiamo che una variabile, X, faccia sì che la variabile Y assuma un valore pari a cos(X).
Per esempio:
- Se X = -10 allora Y = cos(-10) = -0,83907
- Se X = 0 allora Y = cos(0) = 1
- Se X = 10 allora Y = cos(10) = -0,83907
E così via.
Se tracciassimo la relazione tra X e Y, sarebbe simile a questa:
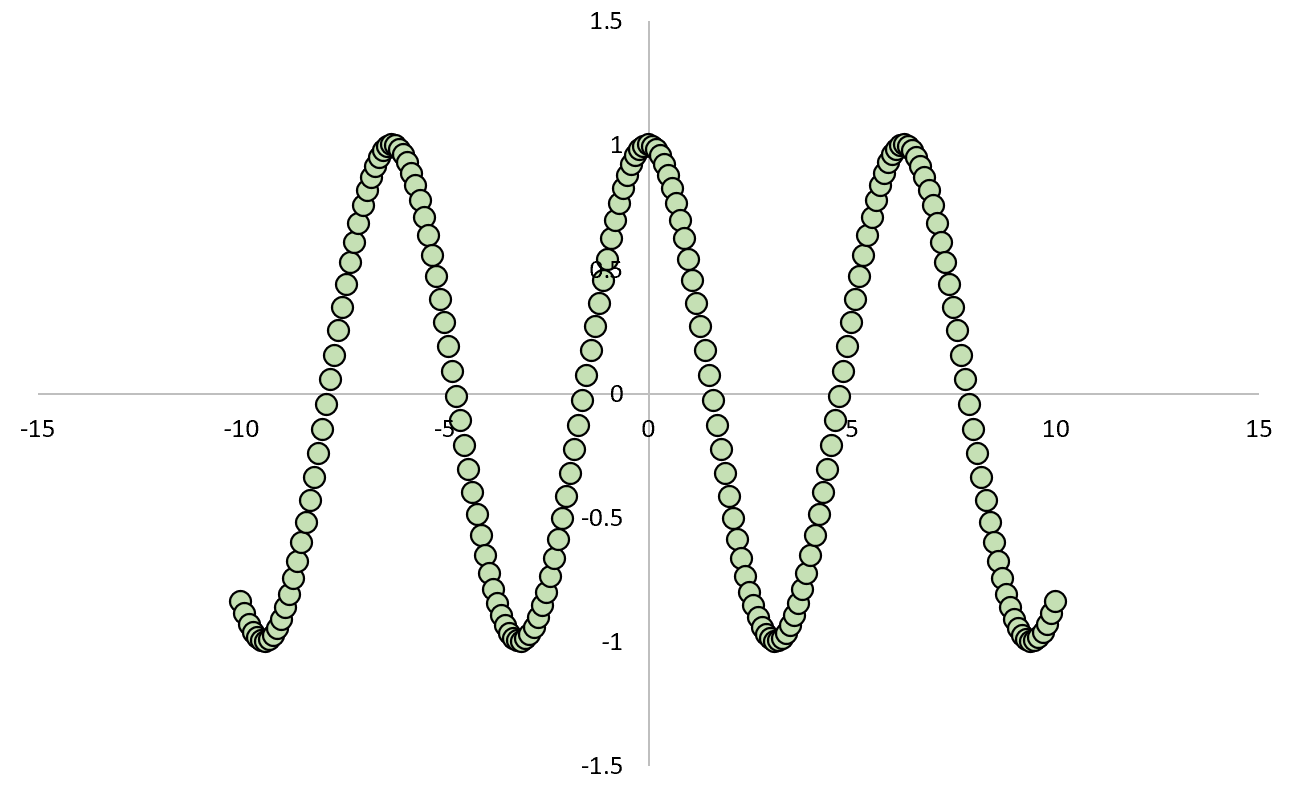
Se calcolassimo il coefficiente di correlazione di Pearson tra le due variabili, troveremmo che la correlazione è zero .
Sappiamo che X causa Y, ma la correlazione lineare tra le due variabili è zero.
Risorse addizionali
Le esercitazioni seguenti forniscono informazioni aggiuntive sulla correlazione e sulla causalità:
La correlazione non implica causalità: 5 esempi concreti
Introduzione al coefficiente di correlazione di Pearson
Causalità inversa: definizione ed esempi
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più