La distribuzione normale

La distribuzione normale è la distribuzione di probabilità più comune nelle statistiche.

Le distribuzioni normali hanno le seguenti caratteristiche:

• Forma a campana
• Simmetrico
• La media e la mediana sono uguali; entrambi si trovano al centro della distribuzione
• Circa il 68% dei dati rientra in una deviazione standard della media
• Circa il 95% dei dati rientra nelle due deviazioni standard della media.
• Circa il 99,7% dei dati rientra nelle tre deviazioni standard della media.

Gli ultimi tre punti sono conosciuti come regola pratica , a volte chiamata regola 68-95-99.7 .

Correlato: Regola empirica (problemi pratici)

Come disegnare una curva normale

Per disegnare una curva normale, dobbiamo conoscere la media e la deviazione standard.

Esempio 1: supponiamo che l’altezza degli uomini in una certa scuola sia distribuita normalmente con una media di $\mu =\; 70\; pollici\; e$ una deviazione standard di $\sigma \; =\; 2\; pollici.\; Disegna\; la\; curva\; normale.$

Passaggio 1: traccia una curva normale.

Passaggio 2: la media di 70 pollici è al centro.

Passaggio 3: ciascuna deviazione standard corrisponde a una distanza di 2 pollici.

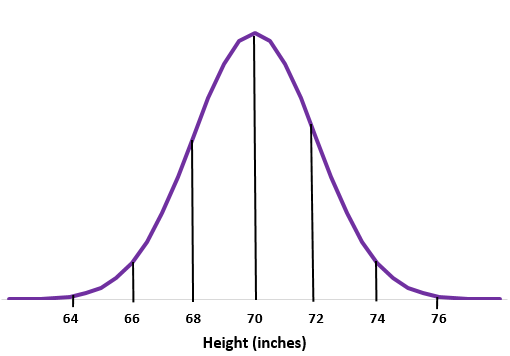
Esempio 2: supponiamo che il peso di una certa specie di lontra sia distribuito normalmente con una media di $\mu =\; 30\; libbre\; e$ una deviazione standard di $\sigma \; =\; 5\; libbre.\; Disegna\; la\; curva\; normale.$

Passaggio 1: traccia una curva normale.

Passaggio 2: la media di 30 libbre cade nel mezzo.

Passaggio 3: ciascuna deviazione standard corrisponde a una distanza di 5 libbre

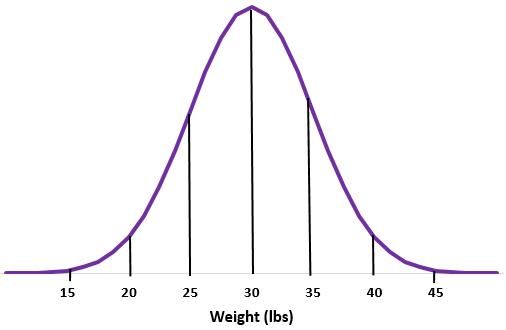
Come trovare le percentuali utilizzando la distribuzione normale

La regola pratica , a volte chiamata regola 68-95-99.7 , afferma che per una variabile casuale distribuita normalmente, il 68% dei dati rientra in un intervallo di una deviazione standard dalla media, il 95% rientra in un intervallo di due deviazioni standard le deviazioni dalla media e il 99,7% sono entro tre deviazioni standard dalla media.

Usando questa regola possiamo rispondere a domande sulle percentuali.

Esempio: supponiamo che l’altezza degli uomini in una certa scuola sia distribuita normalmente con una media di $\mu =\; 70\; pollici\; e$ una deviazione standard di $\sigma \; =\; 2\; pollici.$

$Approssimativamente,\; quale\; percentuale\; di\; uomini\; in\; questa\; scuola\; è\; alta\; più\; di\; 74\; pollici?$

Soluzione:

Passaggio 1: traccia una distribuzione normale con una media di $\mu =\; 70\; pollici\; e$ una deviazione standard di $\sigma \; =\; 2\; pollici.$

Passaggio 2: un’altezza di 74 pollici è due deviazioni standard sopra la media. Aggiungi le percentuali sopra questo punto nella distribuzione normale.

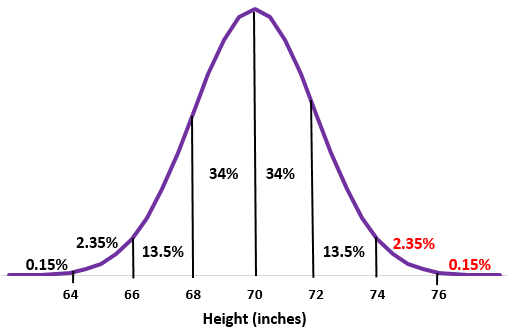
2,35% + 0,15% = 2,5%

Circa il 2,5% degli uomini in questa scuola sono alti più di 74 pollici.

$Approssimativamente\; quale\; percentuale\; di\; uomini\; in\; questa\; scuola\; è\; alta\; tra\; 68\; pollici\; e\; 72\; pollici?$

Soluzione:

Passaggio 1: traccia una distribuzione normale con una media di $\mu =\; 70\; pollici\; e$ una deviazione standard di $\sigma \; =\; 2\; pollici.$

Passaggio 2: un’altezza di 68 pollici e 72 pollici è rispettivamente una deviazione standard sotto e sopra la media. Basta aggiungere le percentuali tra questi due punti nella distribuzione normale.

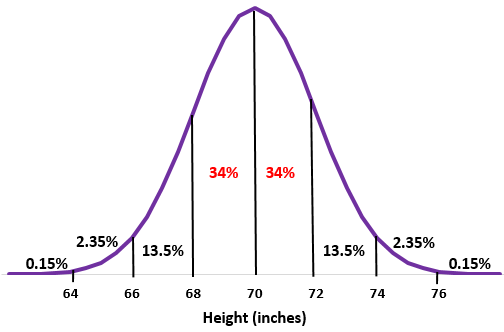
34% + 34% = 68%

Circa il 68% degli uomini in questa scuola sono alti tra 68 pollici e 72 pollici.

Come trovare i conteggi utilizzando la distribuzione normale

Possiamo anche usare la regola pratica per rispondere a domande sui conteggi.

Esempio: supponiamo che il peso di una certa specie di lontra sia distribuito normalmente con una media di $\mu =\; 30\; libbre\; e$ una deviazione standard di $\sigma \; =\; 5\; libbre.$

Una certa colonia ha 200 di queste lontre. Approssimativamente quante di queste lontre pesano più di 35 libbre?

Soluzione:

Passaggio 1: traccia una distribuzione normale con una media di $\mu =\; 30\; lb\; e$ una deviazione standard di $\sigma \; =\; 5\; lb.$

Passaggio 2: un peso di 35 libbre è una deviazione standard sopra la media. Aggiungi le percentuali sopra questo punto nella distribuzione normale.

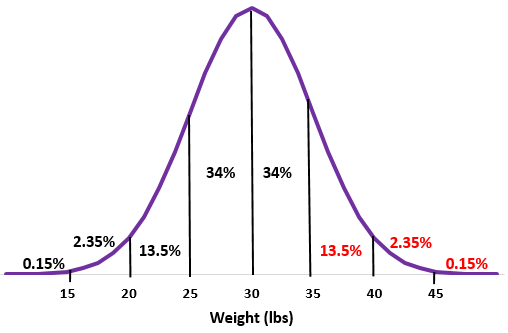
13,5% + 2,35% + 0,15% = 16%

Passo 3: Poiché nella colonia ci sono 200 lontre, 16% di 200 = 0,16 * 200 = 32

Circa 32 lontre in questa colonia pesano più di 35 libbre.

Approssimativamente quante lontre in questa colonia pesano meno di 30 libbre?

Invece di seguire tutti i passaggi appena descritti sopra, possiamo riconoscere che la mediana di una distribuzione normale è uguale alla media, che in questo caso è 30 libbre.

Ciò significa che metà delle lontre pesa più di 30 libbre e l’altra metà pesa meno di 30 libbre. Ciò significa che il 50% delle 200 lontre pesa meno di 30 libbre, quindi 0,5 * 200 = 100 lontre .

Risorse addizionali

I seguenti tutorial forniscono informazioni aggiuntive sulla distribuzione normale:

6 esempi concreti della distribuzione normale
Distribuzione normale vs distribuzione t: la differenza
Come creare una curva a campana in Excel
Come creare una curva a campana in Python