La varianza può essere negativa?
In statistica, il termine varianza si riferisce al modo in cui i valori sono distribuiti in un dato set di dati.
Una domanda comune che gli studenti pongono sulla varianza è:
La varianza può essere negativa?
La risposta: No, la varianza non può essere negativa. Il valore più basso che può assumere è zero.
Per capire perché questo è il caso, dobbiamo capire come viene effettivamente calcolata la varianza.
Come calcolare il divario
La formula per trovare la varianza di un campione (indicata con s 2 ) è:
s2 = Σ (x i – x ) 2 / (n-1)
Oro:
- x : Il campione significa
- x i : L’ i-esima osservazione nel campione
- N : dimensione del campione
- Σ : simbolo greco che significa “somma”
Ad esempio, supponiamo di avere il seguente set di dati con 10 valori:
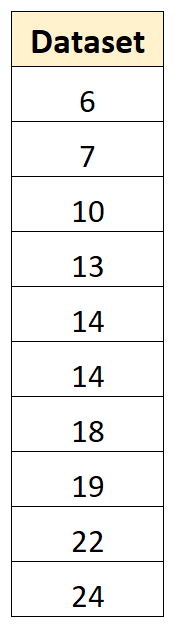
Possiamo utilizzare i seguenti passaggi per calcolare la varianza di questo campione:
Passaggio 1: trova la media
La media è semplicemente la media. Risulta essere 14.7 .
Passaggio 2: trova le deviazioni quadrate
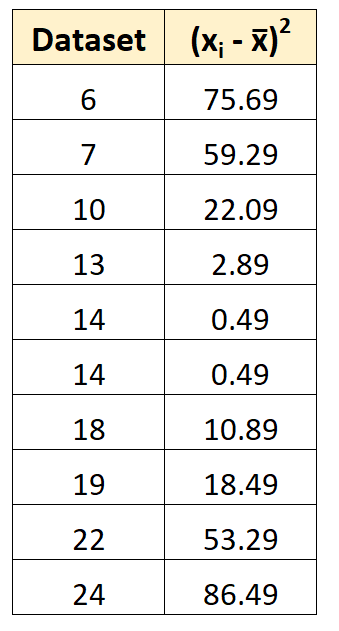
Quindi possiamo calcolare la deviazione quadrata di ogni singolo valore dalla media.
Ad esempio, la prima deviazione quadrata viene calcolata come (6-14,7) 2 = 75,69.
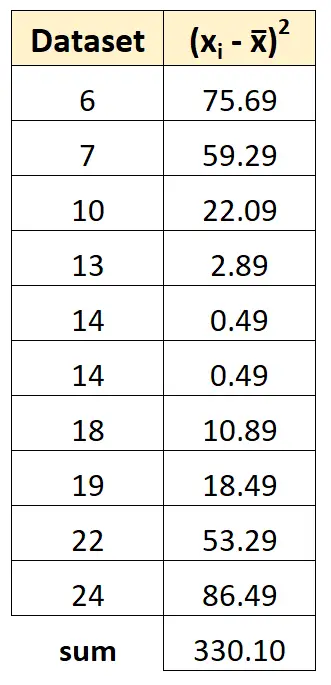
Passaggio 3: Trova la somma delle deviazioni quadrate
Quindi possiamo sommare tutti i quadrati delle deviazioni:
Passaggio 4: calcolare la varianza del campione
Infine, possiamo calcolare la varianza campionaria come la somma delle deviazioni quadrate divisa per (n-1):
s2 = 330,1 / (10-1) = 330,1 / 9 = 36,678
La varianza campionaria risulta essere 36.678 .
Un esempio di varianza zero
L’unico modo in cui un set di dati ha una varianza pari a zero è che tutti i valori nel set di dati siano uguali .
Ad esempio, il seguente set di dati ha una varianza campionaria pari a zero:
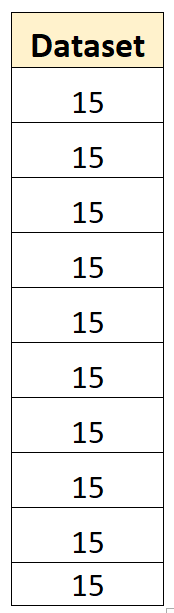
La media del set di dati è 15 e nessuno dei singoli valori si discosta dalla media. Pertanto, la somma dei quadrati delle deviazioni sarà zero e la varianza campionaria sarà semplicemente zero.
La deviazione standard può essere negativa?
Un modo più comune per misurare la distribuzione dei valori in un set di dati è utilizzare la deviazione standard, che è semplicemente la radice quadrata della varianza.
Ad esempio, se la varianza di un dato campione è s2 = 36.678 , la deviazione standard (scritta s ) viene calcolata come segue:
s = √ s2 = √ 36.678 = 6.056
Poiché sappiamo già che la varianza è sempre zero o un numero positivo, ciò significa che la deviazione standard non può mai essere negativa poiché la radice quadrata di zero o di un numero positivo non può essere negativa.
Risorse addizionali
Misure di tendenza centrale: definizione ed esempi
Misure di dispersione: definizione ed esempi
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più