La curtosi può essere negativa?

In statistica, la curtosi viene utilizzata per descrivere la forma di una distribuzione di probabilità.

Nello specifico, ci dice quanto bene i valori dei dati si raggruppano nelle code o nella parte superiore di una distribuzione.

La curtosi di una distribuzione può essere negativa, zero o positiva.

Kurtosi zero

Se una distribuzione ha una curtosi pari a 0, allora è uguale alla distribuzione normale che ha la seguente forma a campana:

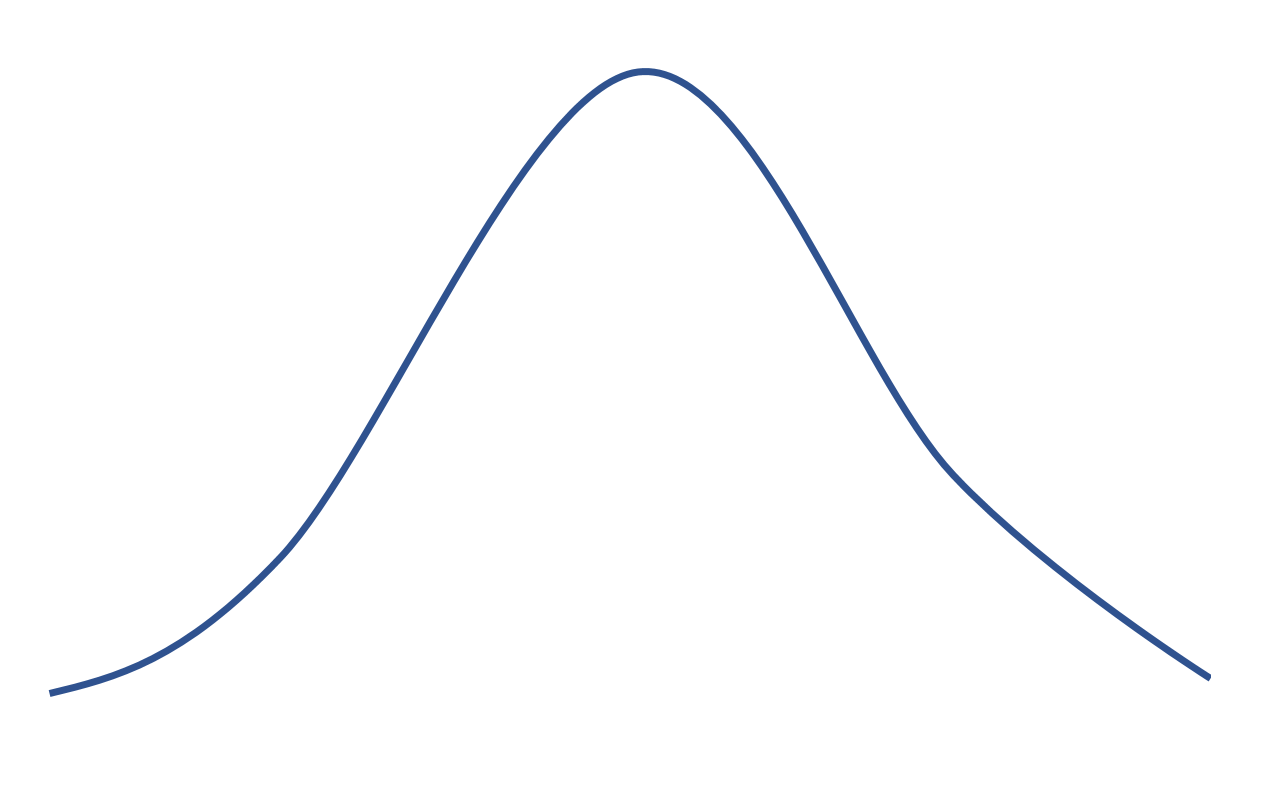
Curtosi positiva

Se una distribuzione ha una curtosi positiva, si dice che sia leptokurtica , nel senso che ha un picco più netto e code più pesanti rispetto a una distribuzione normale.

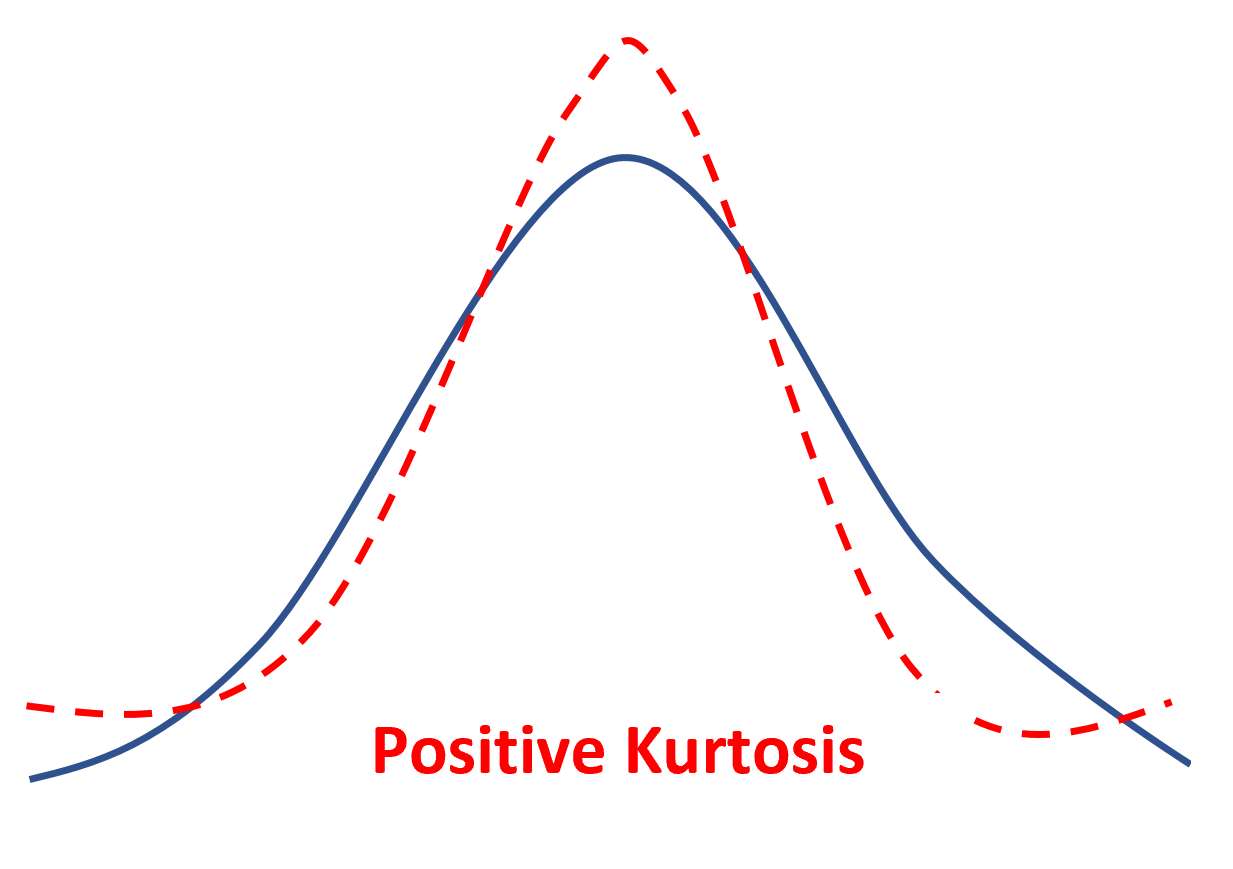
Ciò significa semplicemente che meno valori dei dati si trovano vicino alla media e più valori dei dati si trovano sulle code.

La distribuzione più nota che ha curtosi positiva è la distribuzione t, che ha un picco più netto e code più pesanti rispetto alla distribuzione normale.

Curtosi negativa

Se una distribuzione ha una curtosi negativa, si dice che sia platykurtica , nel senso che ha un picco più piatto e code più sottili rispetto a una distribuzione normale.

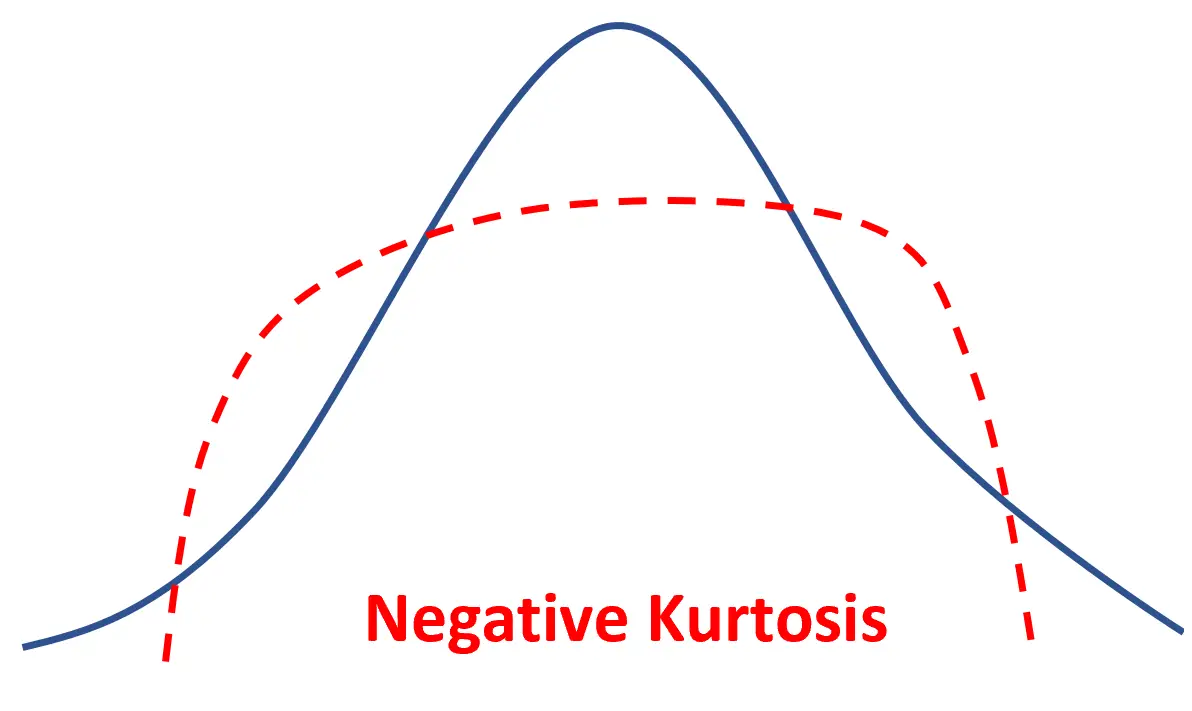
Ciò significa semplicemente che più valori dei dati si trovano vicino alla media e meno valori dei dati si trovano sulle code.

Un esempio estremo di distribuzione che presenta una curtosi negativa è la distribuzione uniforme , che non ha picchi ed è una distribuzione completamente piatta.

Quando usare l’adulazione nella pratica

In pratica, spesso misuriamo la curtosi di una distribuzione nella fase esplorativa dell’analisi quando stiamo semplicemente cercando di comprendere meglio i dati.

Quindi, se vediamo che la curtosi è positiva, sappiamo che stiamo lavorando con una distribuzione che ha meno valori di dati posizionati vicino al centro e più valori di dati distribuiti lungo le code.

Al contrario, se vediamo che la curtosi è negativa, sappiamo che stiamo lavorando con una distribuzione che ha più valori di dati situati vicino al centro e meno valori di dati nelle code.

Risorse addizionali

Per trovare l’asimmetria e la curtosi di una determinata distribuzione, puoi inserire i valori dei dati grezzi in questo calcolatore di asimmetria e curtosi , che ti dirà sia l’asimmetria che la curtosi della distribuzione.

Uno dei test statistici più popolari utilizzati per determinare se una particolare distribuzione presenta o meno asimmetria e curtosi che corrisponde a una distribuzione normale è il test Jarque Bera .

Khan Academy ha anche una bella serie di video che descrivono come classificare le forme di distribuzione.