Legge dei grandi numeri: definizione + esempi

La legge dei grandi numeri afferma che all’aumentare della dimensione del campione, la media campionaria si avvicina al valore atteso.

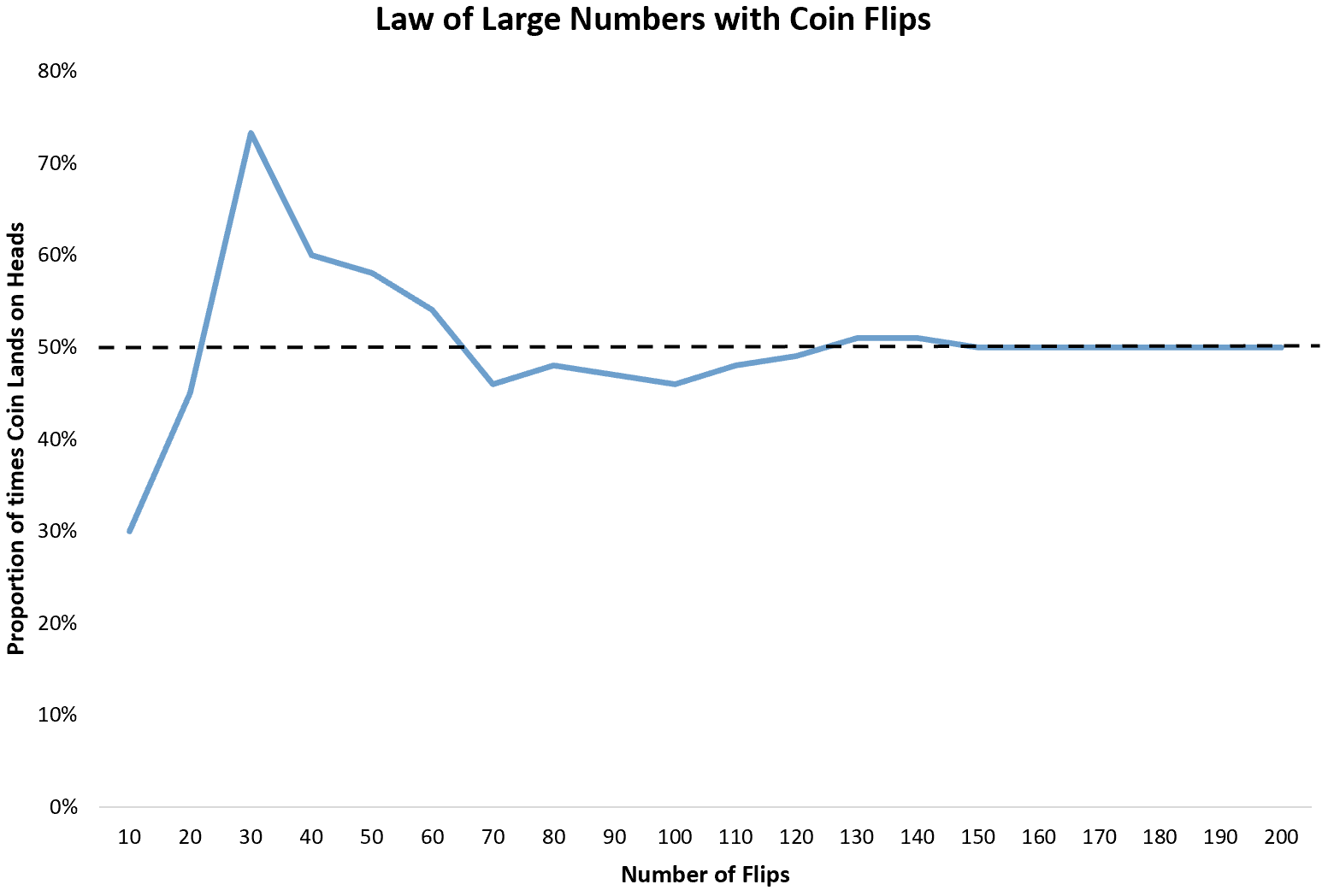
L’esempio più semplice è lanciare una moneta. Ogni volta che lanciamo una moneta, la probabilità che esca testa è 1/2. Quindi la proporzione prevista di teste che appariranno su un numero infinito di lanci è 1/2 o 0,5 .

Tuttavia, se lanciamo una moneta 10 volte, potremmo scoprire che esce testa solo 3 volte. Poiché 10 lanci rappresentano un campione di piccole dimensioni, non vi è alcuna garanzia che la proporzione della testa sia vicina a 0,5 .

Se continuiamo a lanciare la moneta altre 10 volte, potremmo scoprire che esce testa 9 volte su 20. Se la lanciamo altre 10 volte, potremmo scoprire che esce testa 22 volte su 30.

Lanciando la moneta, la proporzione di volte in cui esce testa convergerà alla proporzione prevista di 0,5 .

Questa semplice idea della legge dei grandi numeri viene applicata da molti tipi di aziende e settori nella vita reale.

La legge dei grandi numeri nei casinò

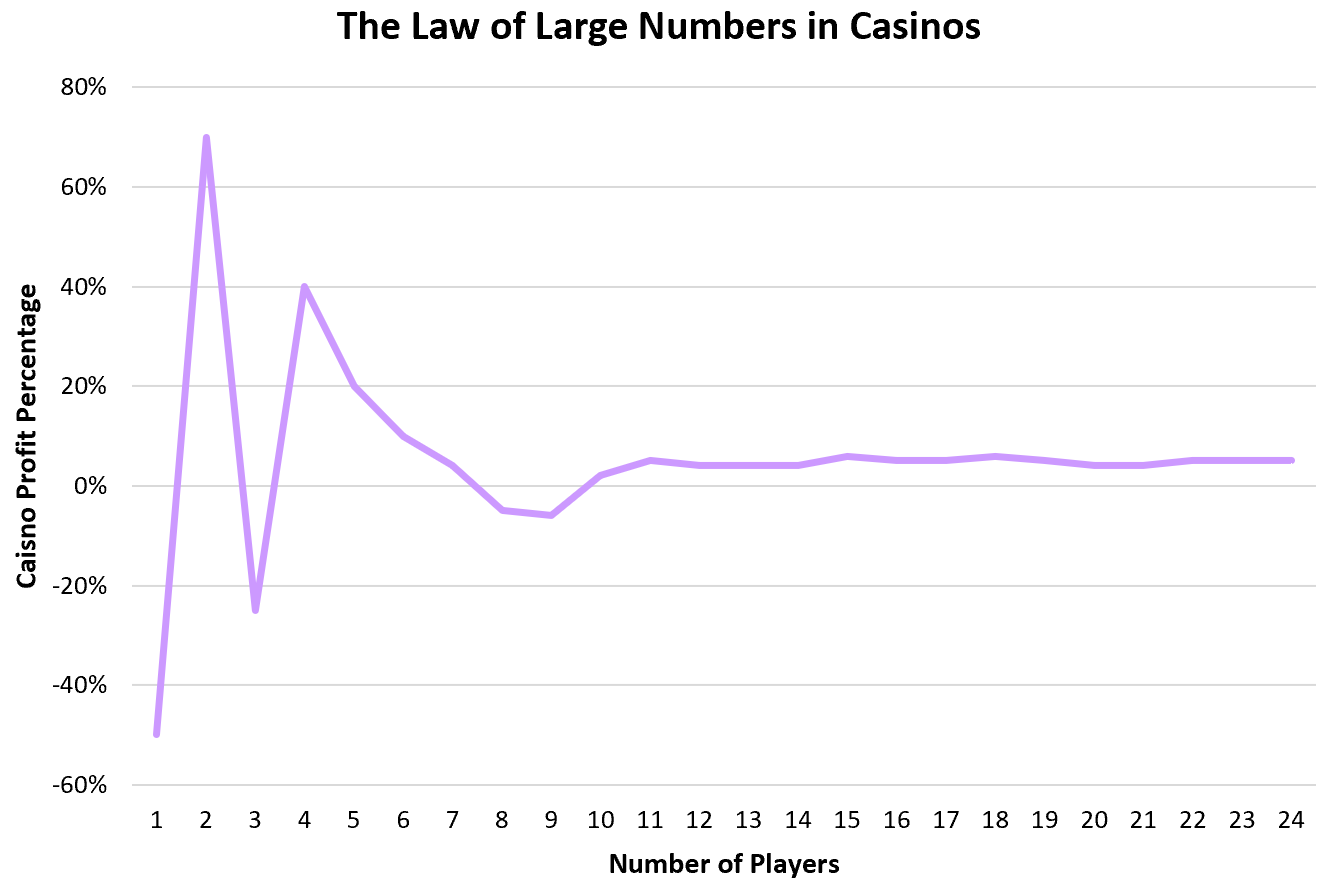
I casinò si affidano alla legge dei grandi numeri per generare profitti in modo affidabile. Per la maggior parte dei giochi, il casinò vince circa il 51-55% delle volte. Ciò significa che gli individui possono essere fortunati e vincere una discreta quantità di tanto in tanto, ma su decine di migliaia di singoli giocatori, il casinò vincerà il previsto 51-55% delle volte.

Ad esempio, Jessica potrebbe giocare ad alcuni giochi al casinò e vincere $ 50.

Mike potrebbe anche giocare qualche gioco e perdere $70.

John potrebbe giocare qualche gioco e vincere $ 25.

Susan potrebbe giocare qualche gioco e perdere $40.

Alcuni giocatori vinceranno soldi e altri perderanno soldi, ma grazie al modo in cui i giochi sono progettati, i casinò possono essere sicuri che vinceranno tra migliaia di individui.

La legge dei grandi numeri nelle assicurazioni

Anche le compagnie di assicurazione si affidano alla legge dei grandi numeri per rimanere redditizie.

L’idea di base è che migliaia di compagnie assicurative possono fornire un’assicurazione a persone che pagano un determinato premio ogni mese e che solo una piccola percentuale delle persone assicurate avrà effettivamente bisogno di utilizzare l’assicurazione per pagare importanti spese impreviste.

Ad esempio, 1.000 persone potrebbero pagare ciascuna 1.000 dollari all’anno per l’assicurazione, il che genererebbe un profitto di 1.000.000 di dollari per una compagnia assicurativa.

Tuttavia, 90 persone potrebbero aver bisogno di ricevere 10.000 dollari ciascuna dalla compagnia assicurativa per coprire spese impreviste relative a vari incidenti, con una conseguente perdita di 900.000 dollari per la compagnia assicurativa.

Alla fine, la compagnia assicurativa realizza un profitto di $ 1.000.000 – $ 900.000 = $ 100.000 .

Ciò significa che la compagnia assicurativa può aspettarsi di realizzare un profitto abbastanza prevedibile, in media, su migliaia di persone.

Si noti che questo modello economico funziona perché una compagnia assicurativa assicura un gran numero di persone . Se assicurassero solo 10 persone, sarebbe troppo rischioso perché una grande spesa imprevista potrebbe spazzare via l’attività.

Pertanto, le compagnie di assicurazione si affidano alla legge dei grandi numeri per prevedere i propri profitti in modo prevedibile.

La legge dei grandi numeri nelle energie rinnovabili

La legge dei grandi numeri viene utilizzata anche dalle società di energia rinnovabile.

L’idea di base è che le turbine eoliche e i pannelli solari possano alimentare i generatori per produrre elettricità in diverse parti dell’azienda. Tuttavia, fuori non c’è né vento né sole, il che significa che le turbine eoliche e i pannelli solari non sono sempre in grado di produrre energia affidabile per i generatori elettrici.

Il modo in cui le aziende di energia rinnovabile aggirano questo problema è connettere decine di migliaia di turbine eoliche o pannelli solari a un’unica rete elettrica, rendendo molto più probabile che queste fonti energetiche producano una quantità affidabile di energia. energia per la rete.

È anche molto più semplice prevedere quanta energia sarà prodotta da queste fonti di energia, poiché gli ingegneri possono semplicemente calcolare la media prevista su decine di migliaia di turbine eoliche o pannelli solari.

Una spiegazione dettagliata di questo fenomeno può essere trovata in questo articolo di Scientific American .