Cos'è un livello beta nelle statistiche? (definizione & #038; esempio)

In statistica, utilizziamo il test di ipotesi per determinare se un’ipotesi su un parametro della popolazione è vera.

Un test di ipotesi ha sempre le seguenti due ipotesi:

Ipotesi nulla (H ₀ ): i dati del campione sono coerenti con la convinzione dominante riguardo al parametro della popolazione.

Ipotesi alternativa ( _HA ): i dati del campione suggeriscono che l’ipotesi espressa nell’ipotesi nulla non è vera. In altre parole, una causa non casuale influenza i dati.

Ogni volta che eseguiamo un test di ipotesi, ci sono sempre quattro possibili risultati:

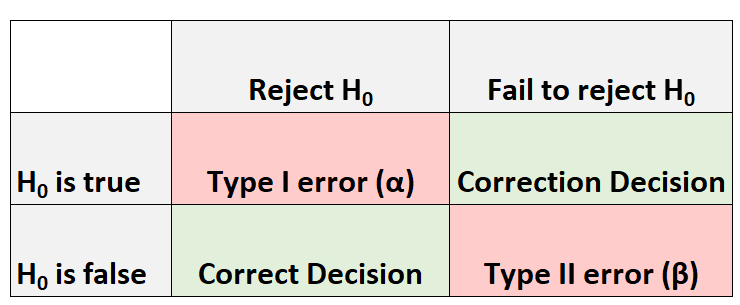
Ci sono due tipi di errori che possiamo commettere:

• Errore di tipo I: rifiutiamo l’ipotesi nulla quando in realtà è vera. La probabilità che si verifichi questo tipo di errore è indicata con α .
• Errore di tipo II: non riusciamo a rifiutare l’ipotesi nulla quando in realtà è falsa. La probabilità di commettere questo tipo di errore viene annotata β .

La relazione tra alfa e beta

Idealmente, i ricercatori vogliono che la probabilità di commettere un errore di tipo I e la probabilità di commettere un errore di tipo II siano basse.

Esiste però un compromesso tra queste due probabilità. Se riduciamo il livello alfa, potremmo diminuire la probabilità di rifiutare un’ipotesi nulla quando è effettivamente vera, ma ciò in realtà aumenta il livello beta – la probabilità che non riusciamo a rifiutare l’ipotesi nulla quando è sbagliata.

Il rapporto tra potenza e beta

La potenza di un test di ipotesi si riferisce alla probabilità di rilevare un effetto o una differenza quando un effetto o una differenza è effettivamente presente. In altre parole, è la probabilità di rifiutare correttamente un’ipotesi falsa nulla.

Viene calcolato come segue:

Potenza = 1 – β

In generale, i ricercatori vogliono che la potenza di un test sia elevata in modo che, se c’è un effetto o una differenza, il test sarà in grado di rilevarlo.

Dall’equazione sopra, possiamo vedere che il modo migliore per aumentare la potenza di un test è ridurre il livello beta. E il modo migliore per ridurre il livello beta è solitamente aumentare la dimensione del campione.

Gli esempi seguenti mostrano come calcolare il livello beta di un test di ipotesi e dimostrano perché l’aumento della dimensione del campione può ridurre il livello beta.

Esempio 1: calcolare Beta per un test di ipotesi

Supponiamo che un ricercatore voglia verificare se il peso medio degli oggetti prodotti in una fabbrica è inferiore a 500 once. Sappiamo che la deviazione standard dei pesi è di 24 once e il ricercatore decide di raccogliere un campione casuale di 40 widget.

Realizzerà la seguente ipotesi a α = 0,05:

• _H0 : µ = 500
• H _A : μ < 500

Ora immagina che il peso medio dei widget prodotti sia in realtà di 490 once. In altre parole, l’ipotesi nulla deve essere respinta.

Possiamo utilizzare i seguenti passaggi per calcolare il livello beta, ovvero la probabilità di non rifiutare l’ipotesi nulla quando in realtà dovrebbe essere rifiutata:

Passaggio 1: trova la regione di non rifiuto.

Secondo il calcolatore del valore critico Z, il valore critico sinistro ad α = 0,05 è -1,645 .

Passaggio 2: trovare il campione minimo che non riusciremo a rifiutare.

La statistica del test è calcolata come z = ( x – μ) / (s/ √n )

Quindi, possiamo risolvere questa equazione per la media campionaria:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/ √40 )
• x = 493.758

Passaggio 3: determinare la probabilità che si verifichi effettivamente la media campionaria minima.

Possiamo calcolare questa probabilità come segue:

• P(Z ≥ (493.758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Secondo il normale calcolatore CDF , la probabilità che Z ≥ 0,99 è 0,1611 .

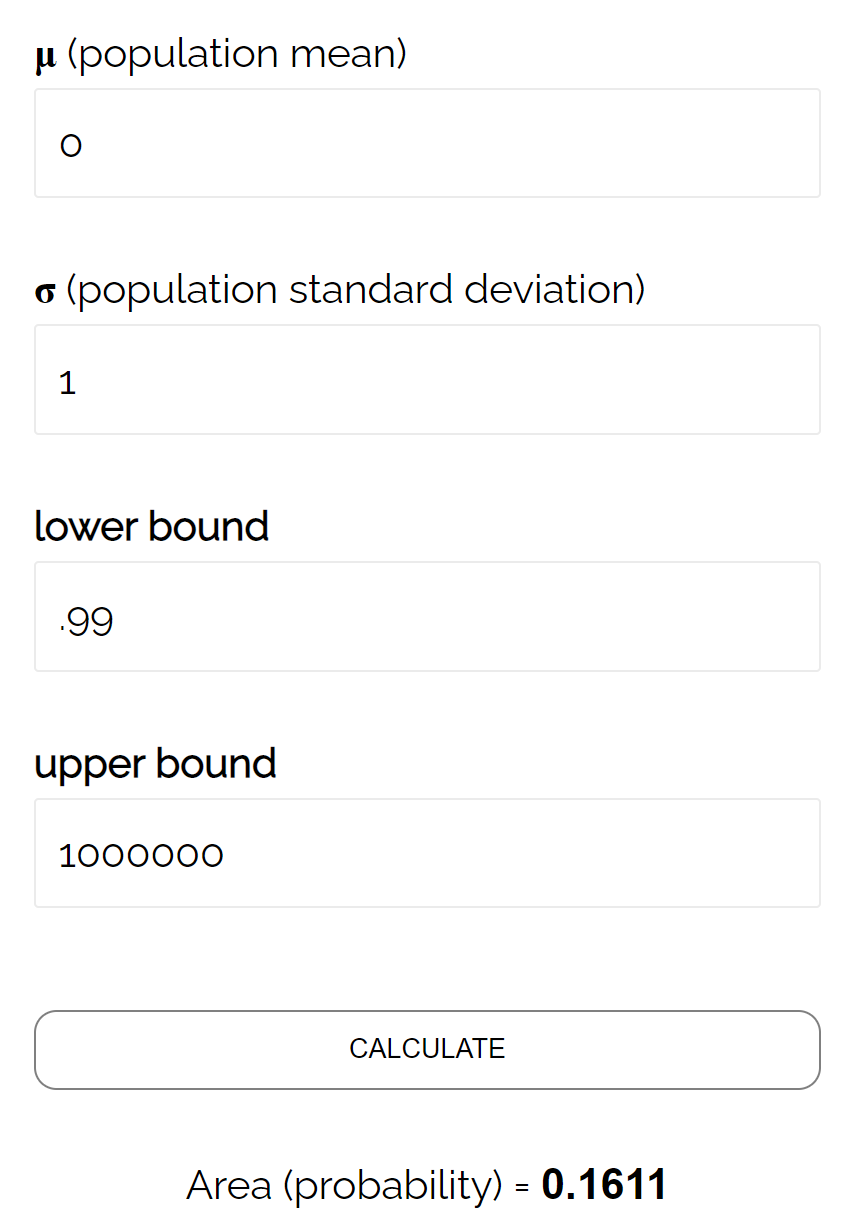
Pertanto, il livello beta per questo test è β = 0,1611. Ciò significa che esiste una probabilità del 16,11% di non rilevare la differenza se la media effettiva è di 490 once.

Esempio 2: calcolare il beta per un test con una dimensione campione maggiore

Supponiamo ora che il ricercatore esegua esattamente lo stesso test di ipotesi, ma utilizzi invece un campione di n = 100 widget. Possiamo ripetere gli stessi tre passaggi per calcolare il livello beta per questo test:

Passaggio 1: trova la regione di non rifiuto.

Secondo il calcolatore del valore critico Z, il valore critico sinistro ad α = 0,05 è -1,645 .

Passaggio 2: trovare il campione minimo che non riusciremo a rifiutare.

La statistica del test è calcolata come z = ( x – μ) / (s/ √n )

Quindi, possiamo risolvere questa equazione per la media campionaria:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/√ 100 )
• x = 496,05

Passaggio 3: determinare la probabilità che si verifichi effettivamente la media campionaria minima.

Possiamo calcolare questa probabilità come segue:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Secondo il normale calcolatore CDF , la probabilità che Z ≥ 2,52 è 0,0059.

Pertanto, il livello beta per questo test è β = 0,0059. Ciò significa che c’è solo una probabilità dello 0,59% di non rilevare la differenza se la media effettiva è di 490 once.

Si noti che semplicemente aumentando la dimensione del campione da 40 a 100, il ricercatore è stato in grado di ridurre il livello beta da 0,1611 a 0,0059.

Bonus: utilizza questo calcolatore di errori di tipo II per calcolare automaticamente il livello beta di un test.

Risorse addizionali

Introduzione al test di ipotesi
Come scrivere un’ipotesi nulla (5 esempi)
Una spiegazione dei valori P e della significatività statistica