Mae contro rmse: quale metrica dovresti utilizzare?

I modelli di regressione vengono utilizzati per quantificare la relazione tra una o più variabili predittive e una variabile di risposta .

Ogni volta che adattiamo un modello di regressione, vogliamo capire quanto bene il modello è in grado di utilizzare i valori delle variabili predittive per prevedere il valore della variabile di risposta.

Due parametri che utilizziamo spesso per quantificare la precisione con cui un modello si adatta a un set di dati sono l’errore medio assoluto (MAE) e l’errore quadratico medio (RMSE), che vengono calcolati come segue:

MAE : una metrica che ci indica la differenza media assoluta tra i valori previsti e i valori effettivi in un set di dati. Più basso è il MAE, migliore è il modello che si adatta al set di dati.

MAE = 1/n * Σ|y _i – ŷ _i |

Oro:

• Σ è un simbolo che significa “somma”
• y _i è il valore osservato per l’ ^i-esima osservazione
• ŷ _i è il valore previsto per l’ ^iesima osservazione
• n è la dimensione del campione

RMSE : una metrica che ci indica la radice quadrata della differenza quadratica media tra i valori previsti e i valori effettivi in un set di dati. Più basso è l’RMSE, migliore è l’adattamento del modello al set di dati.

Viene calcolato come segue:

RMSE = √ Σ(y _i – ŷ _i ) ² / n

Oro:

• Σ è un simbolo che significa “somma”
• ŷ _i è il valore previsto per l’ ^iesima osservazione
• y _i è il valore osservato per l’ ^i-esima osservazione
• n è la dimensione del campione

Esempio: calcolo di RMSE e MAE

Supponiamo di utilizzare un modello di regressione per prevedere quanti punti segneranno 10 giocatori in una partita di basket.

La tabella seguente mostra i punti previsti dal modello rispetto ai punti effettivi segnati dai giocatori:

Utilizzando il calcolatore MAE, possiamo calcolare che il MAE è 3,2.

Questo ci dice che la differenza media assoluta tra i valori previsti dal modello e i valori effettivi è 3,2.

Utilizzando il calcolatore RMSE , possiamo calcolare che l’RMSE è uguale a 4 .

Questo ci dice che la radice quadrata della differenza quadratica media tra i punti segnati previsti e i punti segnati effettivi è 4.

Tieni presente che ogni metrica ci dà un’idea della differenza tipica tra il valore previsto dal modello e il valore effettivo nel set di dati, ma l’interpretazione di ciascuna metrica è leggermente diversa.

RMSE vs. MAE: quale metrica dovresti utilizzare?

Se si desidera assegnare più peso alle osservazioni più lontane dalla media (ovvero se una deviazione di 20 è più del doppio di una deviazione di 10), è meglio utilizzare l’RMSE per misurare l’errore, perché l’RMSE è più sensibile alle osservazioni più lontane dalla media.

Tuttavia, se essere “compensato” a 20 è due volte più dannoso che essere “compensato” a 10, allora è meglio usare il MAE.

Per illustrare ciò, supponiamo di avere un giocatore che è un chiaro valore anomalo in termini di numero di punti segnati:

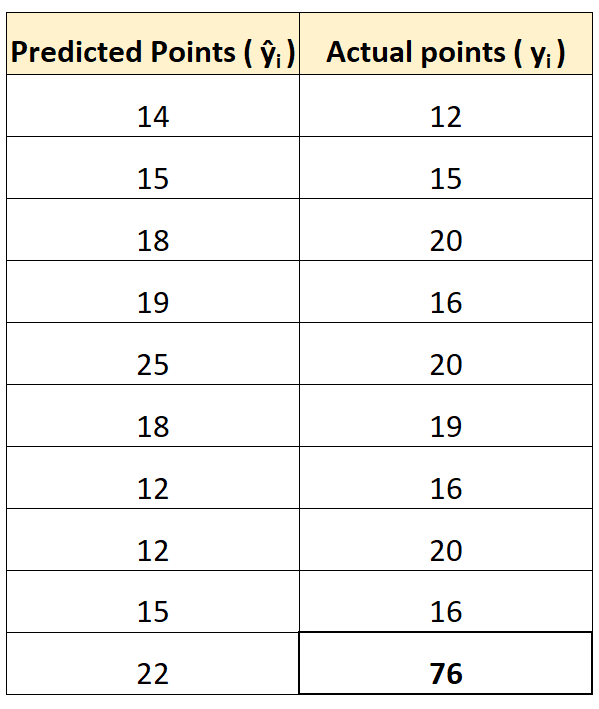
Utilizzando i calcolatori online menzionati in precedenza, possiamo calcolare MAE e RMSE come:

• MAE : 8
• RMSE : 16.4356

Si noti che l’RMSE aumenta molto più del MAE.

Questo perché RMSE utilizza le differenze al quadrato nella sua formula e la differenza al quadrato tra il valore osservato di 76 e il valore previsto di 22 è piuttosto ampia. Ciò si traduce in un aumento significativo del valore RMSE.

In pratica, in genere adattiamo più modelli di regressione a un set di dati e calcoliamo solo uno di questi parametri per ciascun modello.

Ad esempio, potremmo adattare tre diversi modelli di regressione e calcolare l’RMSE per ciascun modello. Selezioneremo quindi il modello con il valore RMSE più basso come modello “migliore”, perché è quello che fa le previsioni più vicine ai valori effettivi nel set di dati.

In entrambi i casi, assicurati solo di calcolare la stessa metrica per ciascun modello. Ad esempio, non calcolare il MAE per un modello e l’RMSE per un altro modello e quindi confrontare queste due misurazioni.

Risorse addizionali

I seguenti tutorial spiegano come calcolare il MAE utilizzando diversi software statistici:

Come calcolare l’errore assoluto medio in Excel
Come calcolare l’errore medio assoluto in R
Come calcolare l’errore assoluto medio in Python

I seguenti tutorial spiegano come calcolare l’RMSE utilizzando diversi software statistici:

Come calcolare l’errore quadratico medio in Excel
Come calcolare l’errore quadratico medio in R
Come calcolare l’errore quadratico medio in Python