Come eseguire un test di mancanza di adattamento in r (passo dopo passo)

Un test di mancanza di adattamento viene utilizzato per determinare se un modello di regressione completo fornisce o meno un adattamento significativamente migliore a un set di dati rispetto a una versione ridotta del modello.

Ad esempio, supponiamo di voler utilizzare il numero di ore di studio per prevedere i punteggi degli esami per gli studenti di un determinato college. Possiamo decidere di adattare i seguenti due modelli di regressione:

Modello completo: punteggio = β ₀ + B ₁ (ore) + B ₂ (ore) ²

Modello ridotto: punteggio = β ₀ + B ₁ (ore)

Il seguente esempio dettagliato mostra come eseguire un test di adattamento per mancanza in R per determinare se il modello completo fornisce un adattamento significativamente migliore rispetto al modello ridotto.

Passaggio 1: crea e visualizza un set di dati

Innanzitutto, utilizzeremo il seguente codice per creare un set di dati contenente il numero di ore studiate e i punteggi degli esami ottenuti per 50 studenti:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Successivamente, creeremo un grafico a dispersione per visualizzare la relazione tra ore e punteggio:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

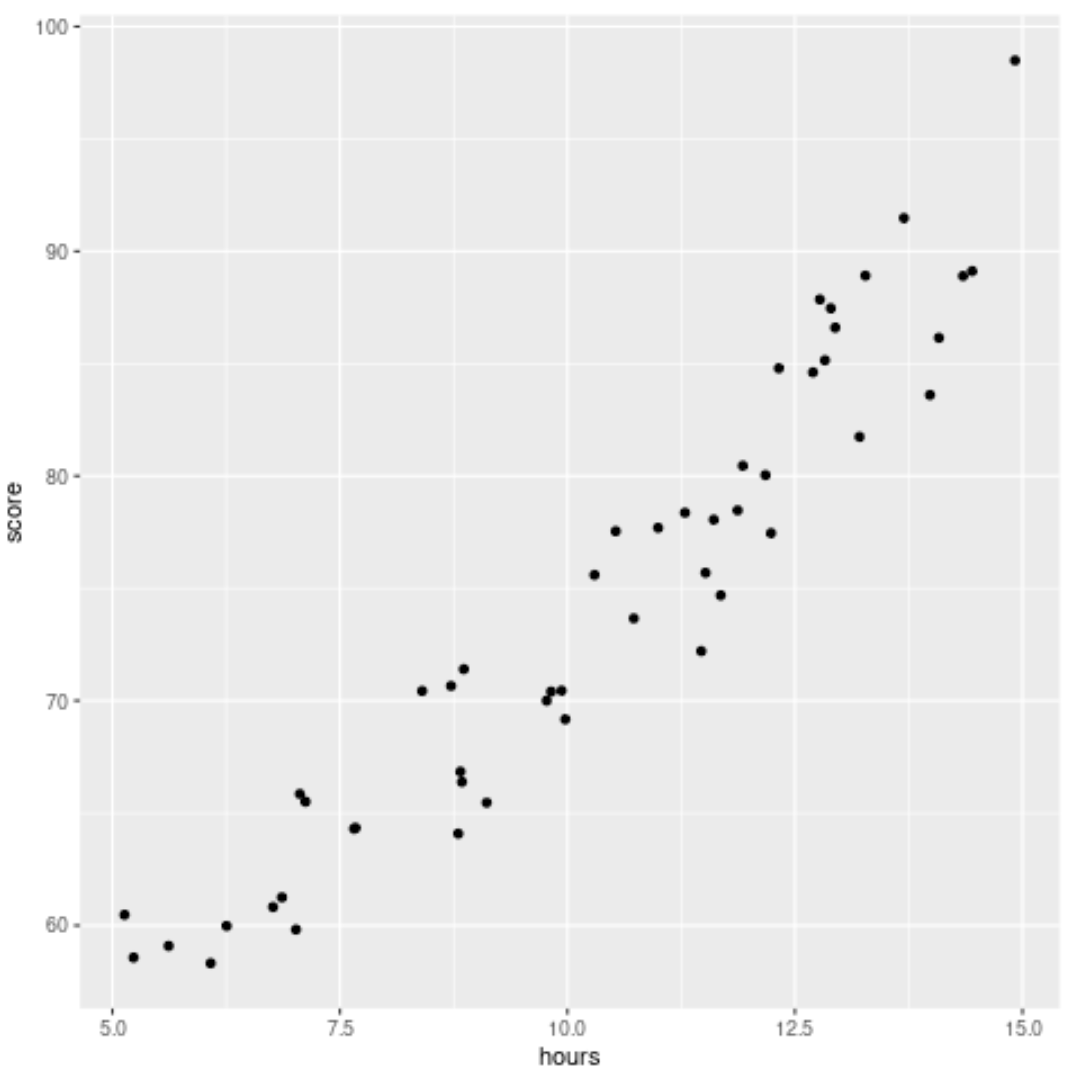
Passaggio 2: adattare due modelli diversi al set di dati

Successivamente, adatteremo due diversi modelli di regressione al set di dati:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

Passaggio 3: eseguire un test di idoneità

Successivamente, utilizzeremo il comando anova() per eseguire un test di adattamento tra i due modelli:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La statistica del test F risulta essere 10,554 e il corrispondente valore p è 0,002144 . Poiché questo valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla del test e concludere che il modello completo fornisce un adattamento migliore, statisticamente significativo, rispetto al modello ridotto.

Passaggio 4: Visualizza il modello finale

Infine, possiamo visualizzare il modello finale (il modello completo) rispetto al set di dati originale:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

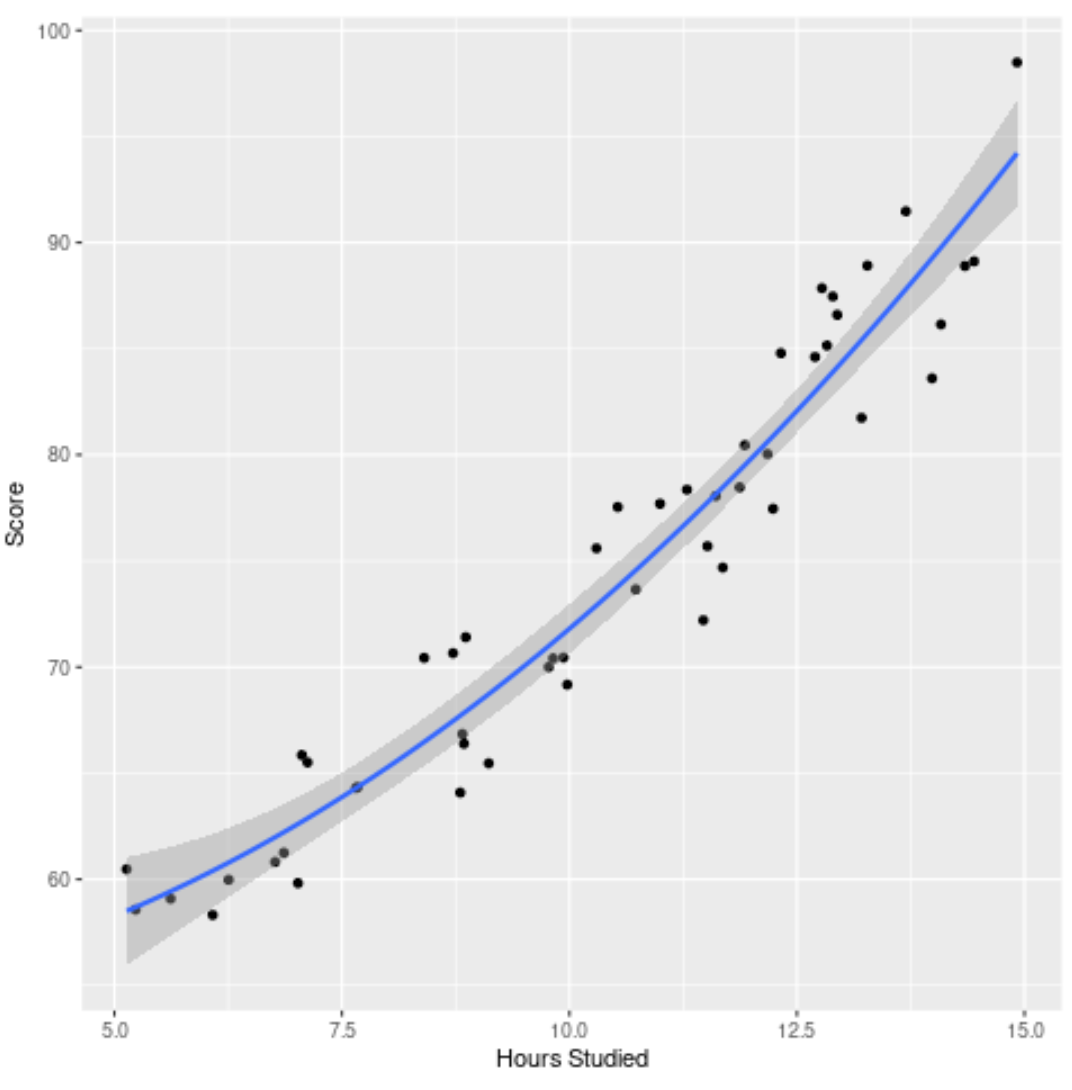
Possiamo vedere che la curva del modello si adatta abbastanza bene ai dati.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione polinomiale in R