Matrice di correlazione

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

In questo articolo scoprirai cos’è una matrice di correlazione, qual è la sua formula e come interpretare una matrice di correlazione. Inoltre, potrai vedere un esempio concreto dell’interpretazione di una matrice di correlazione.

Cos’è una matrice di correlazione?

La matrice di correlazione è una matrice che contiene in posizione i,j il coefficiente di correlazione tra le variabili i e j .

Pertanto, la matrice di correlazione è una matrice quadrata piena di unità sulla diagonale principale e l’elemento della riga i e della colonna j è costituito dal valore del coefficiente di correlazione tra la variabile i e la variabile j .

La formula per la matrice di correlazione è quindi la seguente:

Oro

$r_{ij}$

è il coefficiente di correlazione tra le variabili

$i$

$j.$

Pertanto, per trovare la matrice di correlazione di un set di dati, è essenziale sapere come viene calcolato il coefficiente di correlazione. Nel caso non lo ricordassi, nel seguente link scoprirai come farlo con un calcolatore online:

➤ Vedi: calcolatore del coefficiente di correlazione

Una proprietà del coefficiente di correlazione è che l’ordine delle variabili non ha importanza per il suo calcolo, cioè il coefficiente di correlazione

$r_{ij}$

è equivalente a

$r_{ji}.$

Pertanto, la matrice di correlazione è simmetrica.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

Affinché una matrice di correlazione sia significativa, il set di dati statistici deve avere più di due variabili. Altrimenti basterebbe determinare un unico coefficiente di correlazione e la matrice di correlazione avrebbe senso.

Come costruire una matrice di correlazione

Data la definizione di matrice di correlazione, vediamo come si crea questo tipo di matrice statistica:

Calcolare il coefficiente di correlazione di ciascuna coppia di variabili. Tieni presente che l’ordine delle variabili non cambia il risultato, quindi deve essere calcolato solo una volta per ciascuna coppia di variabili.
Crea una matrice quadrata della stessa dimensione del numero di variabili nella serie di dati. Questa matrice sarà la matrice di correlazione.
Metti un 1 in ciascun elemento della diagonale principale della matrice di correlazione.
Metti il coefficiente di correlazione delle variabili i , j nelle posizioni i , j e j , i .
Una volta creata la matrice di correlazione non resta che interpretarne i valori.

Tieni presente che eseguire semplicemente la matrice di correlazione non è sufficiente, è necessario interpretarne i valori e capire cosa significano. La sezione seguente spiega come interpretare una matrice di correlazione.

Interpretazione della matrice di correlazione

Per interpretare correttamente la matrice di correlazione è necessario tenere conto che il valore del coefficiente di correlazione può variare da -1 a +1:

r=-1 : le due variabili hanno una perfetta correlazione negativa, quindi possiamo tracciare una linea con pendenza negativa in cui tutti i punti si collegano.
-1<r<0 : la correlazione tra le due variabili è negativa, quindi quando una variabile aumenta l’altra diminuisce. Più il valore è vicino a -1, più le variabili sono correlate negativamente.
r=0 : la correlazione tra le due variabili è molto debole, infatti la relazione lineare tra loro è zero. Ciò non significa che le variabili siano indipendenti, poiché potrebbero avere una relazione non lineare.
0<r<1 : la correlazione tra le due variabili è positiva, più il valore è vicino a +1, più forte è la relazione tra le variabili. In questo caso una variabile tende ad aumentare il proprio valore quando aumenta anche l’altra.
r=1 : le due variabili hanno una perfetta correlazione positiva, cioè hanno una relazione lineare positiva.

Pertanto, per interpretare la matrice di correlazione, è necessario interpretare ciascun coefficiente di correlazione e confrontare i diversi risultati.

In questo modo potrai vedere quali variabili sono più correlate tra loro, quali variabili sono le più importanti, quali variabili non hanno praticamente alcuna relazione tra loro, ecc.

Esempio di matrice di correlazione

Per comprendere appieno in cosa consiste la matrice di correlazione e come viene interpretata, in questa sezione analizzeremo un esempio di matrice di correlazione:

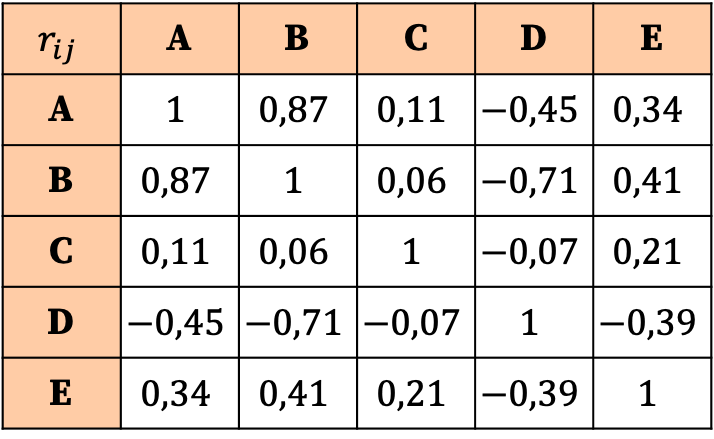
L’interpretazione della matrice di correlazione si basa sui valori dei coefficienti. Pertanto, possiamo vedere che la correlazione più forte è la relazione tra la variabile A e la variabile B, poiché il suo coefficiente corrispondente è il più grande (0,87).

D’altra parte la variabile C non ha praticamente alcuna correlazione con nessuna variabile, poiché tutti i suoi coefficienti sono molto vicini allo zero e quindi molto bassi. Quindi, per semplificare l’analisi, potremmo anche considerare di eliminare questa variabile dallo studio statistico.

Allo stesso modo, tutte le relazioni della variabile D con le altre variabili sono negative, il che significa che la correlazione tra la variabile D e le altre variabili è inversa. Ciò non implica che la variabile debba essere eliminata, ma solo che la variabile D è negativamente correlata.

Come puoi vedere, la matrice di correlazione è molto utile per riassumere i dati e fare un’analisi complessiva della relazione tra le diverse variabili nel dataset.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più