Come creare una matrice di correlazione in r (4 esempi)

Una matrice di correlazione è una tabella quadrata che mostra i coefficienti di correlazione tra le variabili in un set di dati.

Fornisce un modo rapido per comprendere la forza delle relazioni lineari esistenti tra le variabili in un set di dati.

Esistono quattro modi comuni per creare una matrice di correlazione in R:

Metodo 1: la funzione cor (per ottenere una semplice matrice di coefficienti di correlazione)

 cor(df)

Metodo 2: la funzione rcorr (per ottenere i p-value dei coefficienti di correlazione)

 library (Hmisc)

rcorr( as.matrix (df))

Metodo 3: la funzione corrplot (per visualizzare la matrice di correlazione)

 library (corplot)

corrplot(cor(df))

Metodo 4: la funzione ggcorrplot (per visualizzare la matrice di correlazione)

 library (ggcorrplot)

ggcorrplot(cor(df))

Gli esempi seguenti mostrano come utilizzare ciascun metodo con il seguente frame di dati in R:

 #create data frame
df <- data. frame (assists=c(4, 5, 5, 6, 7, 8, 8, 10),
                 rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
                 points=c(22, 24, 26, 26, 29, 32, 20, 14))

#view data frame
df

  assists rebound points
1 4 12 22
2 5 14 24
3 5 13 26
4 6 7 26
5 7 8 29
6 8 8 32
7 8 9 20
8 10 13 14

Esempio 1: la funzione cor

Possiamo utilizzare la funzione R base cor() per creare una matrice di correlazione che mostra i coefficienti di correlazione tra ciascuna variabile nel nostro frame di dati:

 #create correlation matrix
cor(df)

            assists rebound points
assists 1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608 1.0000000 -0.5220917
points -0.3295730 -0.5220917 1.0000000

I coefficienti di correlazione lungo la diagonale della tabella sono tutti pari a 1 perché ogni variabile è perfettamente correlata con se stessa.

Tutti gli altri coefficienti di correlazione indicano la correlazione tra diverse combinazioni di variabili a coppie. Per esempio:

• Il coefficiente di correlazione tra assist e rimbalzi è -0,245 .
• Il coefficiente di correlazione tra assist e punti è -0,330 .
• Il coefficiente di correlazione tra rimbalzi e punti è -0,522 .

Esempio 2: la funzione rcorr

Possiamo utilizzare la funzione rcorr() del pacchetto Hmisc in R per creare una matrice di correlazione che mostri i coefficienti di correlazione tra ciascuna variabile nel nostro frame di dati:

 library (Hmisc)

#create matrix of correlation coefficients and p-values
rcorr( as.matrix (df))

         assists rebound points
assists 1.00 -0.24 -0.33
rebounds -0.24 1.00 -0.52
points -0.33 -0.52 1.00

n=8 

P
         assists rebound points
assists 0.5589 0.4253
rebounds 0.5589 0.1844
points 0.4253 0.1844

La prima matrice mostra i coefficienti di correlazione tra le variabili e la seconda matrice mostra i corrispondenti valori p.

Ad esempio, il coefficiente di correlazione tra assist e rimbalzi è -0,24 e il valore p di questo coefficiente di correlazione è 0,5589 .

Questo ci dice che la correlazione tra le due variabili è negativa ma non è una correlazione statisticamente significativa poiché il valore p non è inferiore a 0,05.

Esempio 3: la funzione corrplot

Possiamo usare la funzione corrplot() dal pacchetto corrplot in R per visualizzare la matrice di correlazione:

 library (corplot)

#visualize correlation matrix
corrplot(cor(df))

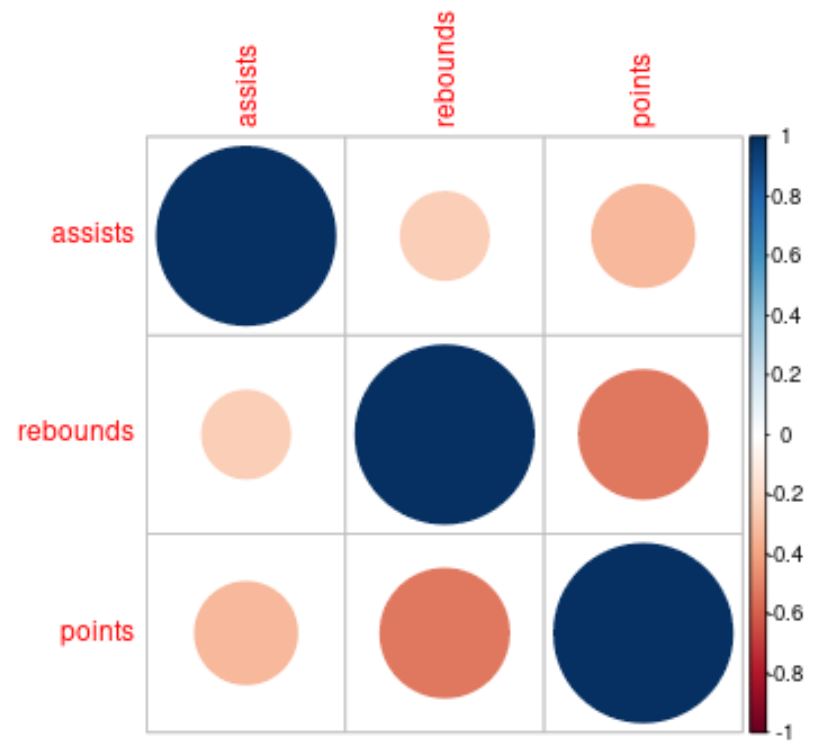
Il colore e la dimensione dei cerchi nella matrice di correlazione ci aiutano a visualizzare le correlazioni tra ciascuna variabile.

Ad esempio, il cerchio in cui si intersecano le variabili assist e rimbalzi è piccolo e rosso chiaro, il che ci dice che la correlazione è debole e negativa.

Esempio 4: la funzione corrplot

Possiamo utilizzare la funzione ggcorrplot() dal pacchetto ggcorrplot in R per visualizzare la matrice di correlazione:

 library (ggcorrplot)

#visualize correlation matrix
ggcorrplot(cor(df))

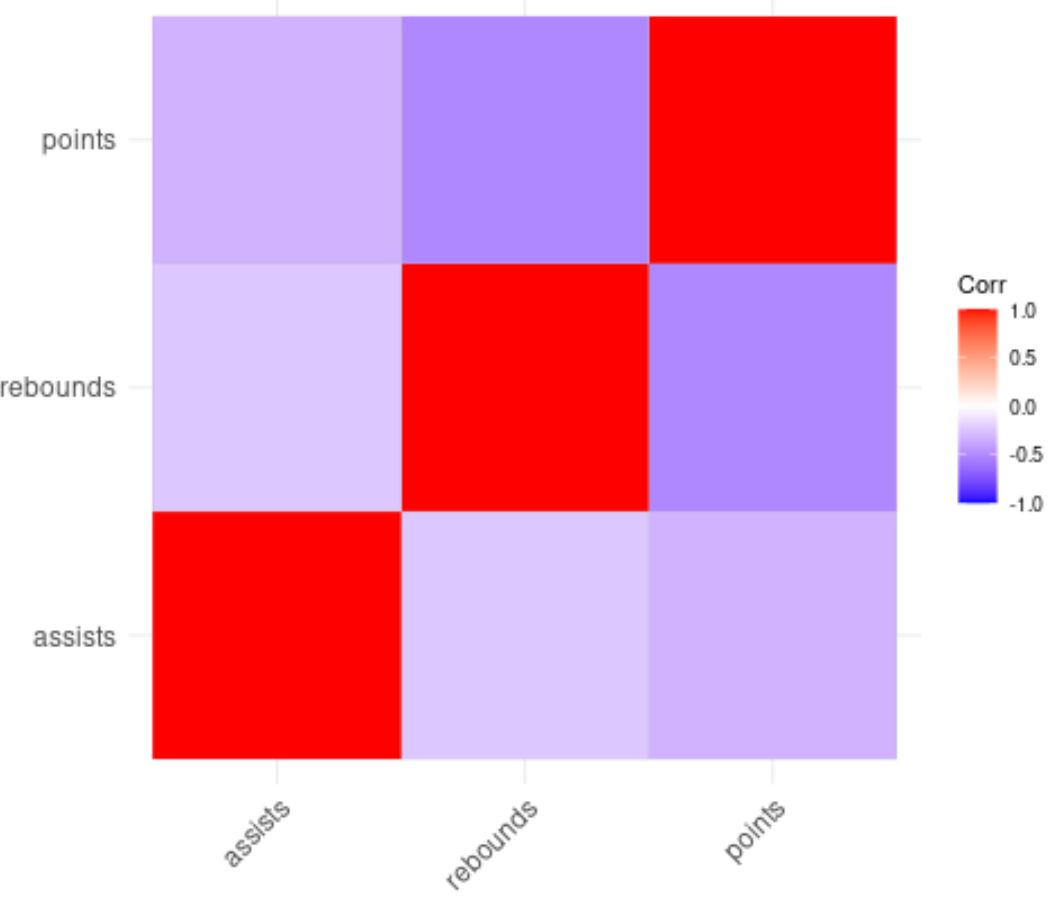
Il colore dei quadrati nella matrice di correlazione ci aiuta a visualizzare le correlazioni tra ciascuna variabile.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come calcolare la correlazione del rango di Spearman in R
Come calcolare la correlazione parziale in R
Come calcolare la correlazione scorrevole in R