Come creare una matrice di covarianza in python

La covarianza è una misura di come i cambiamenti in una variabile sono associati ai cambiamenti in una seconda variabile. Più specificamente, è una misura del grado in cui due variabili sono linearmente associate.

Una matrice di covarianza è una matrice quadrata che mostra la covarianza tra molte variabili diverse. Questo può essere un modo utile per comprendere come le diverse variabili sono correlate in un set di dati.

L’esempio seguente mostra come creare una matrice di covarianza in Python.

Come creare una matrice di covarianza in Python

Utilizzare i passaggi seguenti per creare una matrice di covarianza in Python.

Passaggio 1: crea il set di dati.

Per prima cosa creeremo un set di dati contenente i punteggi dei test di 10 studenti diversi in tre materie: matematica, scienze e storia.

 import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

Passaggio 2: creare la matrice di covarianza.

Successivamente, creeremo la matrice di covarianza per questo set di dati utilizzando la funzione numpy cov() , specificando che bias = True in modo da poter calcolare la matrice di covarianza della popolazione.

 np.cov(data, bias= True )

array([[ 64.96, 33.2, -24.44],
       [33.2, 56.4, -24.1],
       [-24.44, -24.1, 75.56]])

Passaggio 3: Interpretare la matrice di covarianza.

I valori lungo le diagonali della matrice sono semplicemente le varianze di ciascun soggetto. Per esempio:

• La varianza dei punteggi di matematica è 64,96
• La varianza dei punteggi scientifici è 56,4
• La varianza del punteggio storico è 75,56

Gli altri valori della matrice rappresentano le covarianze tra i diversi soggetti. Per esempio:

• La covarianza tra i punteggi di matematica e scienze è 33,2.
• La covarianza tra i punteggi di matematica e storia è -24,44.
• La covarianza tra i punteggi di scienza e storia è -24,1.

Un numero positivo per la covarianza indica che due variabili tendono ad aumentare o diminuire in tandem. Ad esempio, matematica e scienze hanno una covarianza positiva (33,2), indicando che gli studenti che ottengono punteggi elevati in matematica tendono ad ottenere punteggi elevati anche in scienze. Al contrario, gli studenti che ottengono scarsi risultati in matematica tendono ad avere scarsi risultati anche in scienze.

Un numero negativo per la covarianza indica che all’aumentare di una variabile, una seconda variabile tende a diminuire. Ad esempio, matematica e storia hanno una covarianza negativa (-24,44), indicando che gli studenti che ottengono punteggi alti in matematica tendono ad avere punteggi bassi in storia. Al contrario, gli studenti che ottengono punteggi bassi in matematica tendono ad ottenere punteggi alti in storia.

Passaggio 4: Visualizza la matrice di covarianza (facoltativo).

Puoi visualizzare la matrice di covarianza utilizzando la funzione heatmap() del pacchetto seaborn:

 import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

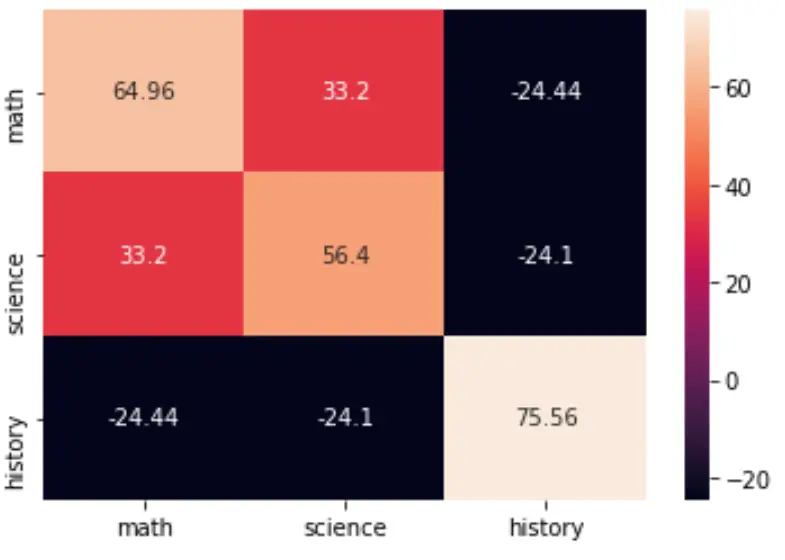
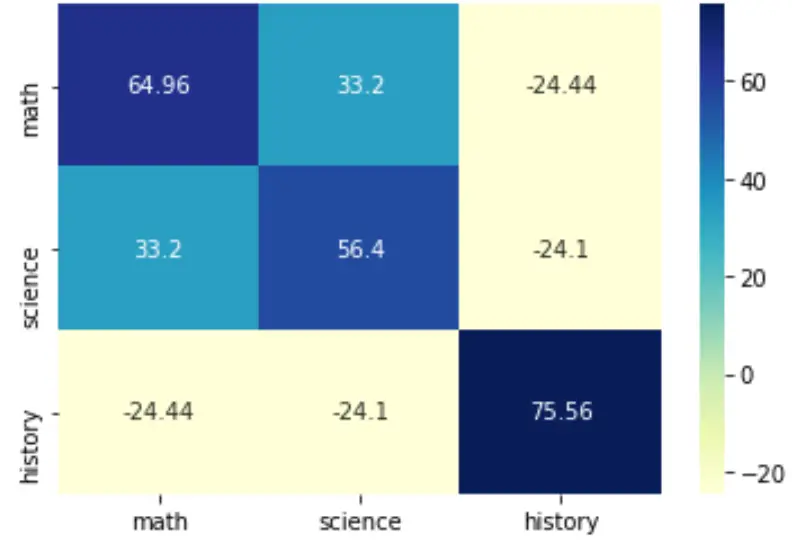
Puoi anche modificare la tavolozza dei colori specificando l’argomento cmap :

 sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show() 

Per maggiori dettagli su come definire lo stile di questa mappa termica, fare riferimento alla documentazione di Seaborn .