Matrice di covarianza

Questo articolo spiega cos’è la matrice di covarianza e qual è la sua formula. Scoprirai come creare la matrice di covarianza con un esempio concreto e le proprietà delle matrici di covarianza.

Cos’è la matrice di covarianza?

La matrice di covarianza è una matrice quadrata i cui elementi sono le varianze e le covarianze delle variabili studiate. Pertanto, gli elementi della diagonale principale della matrice di covarianza rappresentano la varianza di ciascuna variabile e gli elementi rimanenti sono le covarianze tra le variabili.

In statistica, la matrice di covarianza viene utilizzata per analizzare la relazione tra due o più variabili casuali. La matrice di covarianza è molto utile perché permette di interpretare velocemente la correlazione tra molte variabili, poiché è possibile vedere contemporaneamente i valori di tutte le covarianze delle variabili.

Il simbolo della matrice di covarianza è la lettera greca maiuscola sigma (Σ).

Come calcolare la matrice di covarianza

Per calcolare la matrice di covarianza di più variabili statistiche, è necessario eseguire i seguenti passaggi:

1. Calcolare le varianze di tutte le variabili.
2. Calcolare la covarianza di ciascuna coppia di variabili.
3. Forma la matrice di covarianza:
• La varianza della variabile i deve essere collocata sulla diagonale principale della matrice, più precisamente nella posizione i,i .
• La covarianza tra le variabili i e j deve essere messa nella posizione i,j della matrice.

La formula per la matrice di covarianza è quindi la seguente:

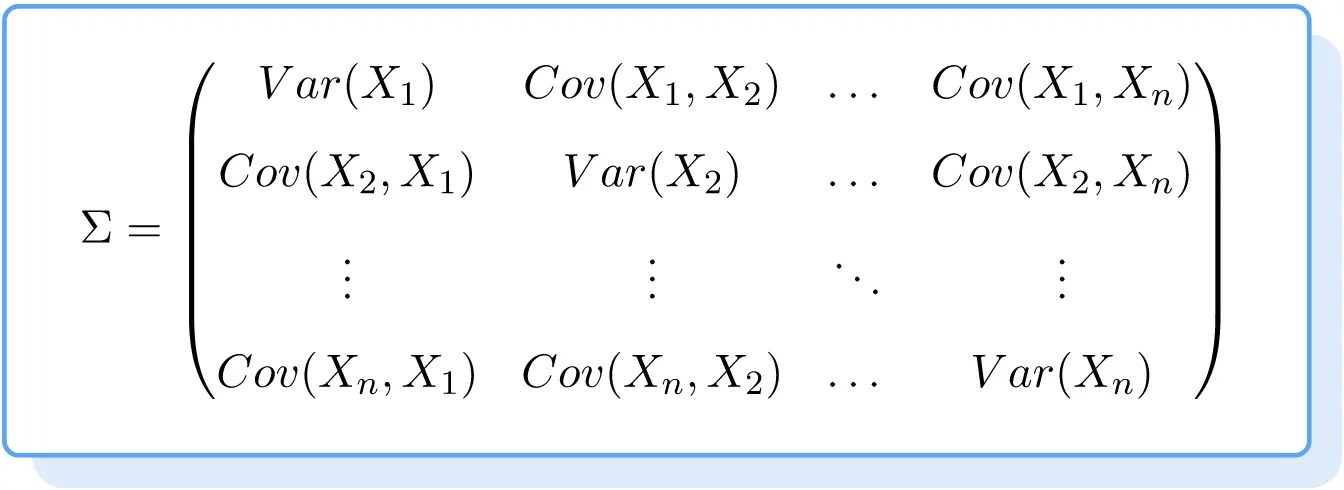
Esempio di matrice di covarianza

Dopo aver visto la definizione di matrice di covarianza, di seguito è riportato un esercizio passo passo in modo da poter vedere come è realizzato questo tipo di matrice.

Calcola la matrice di covarianza delle variabili X, Y e Z, i cui valori sono:

• X: 4, 7, 12, 5, 7
• E: 9, 15, 19, 6, 8
• Z: 7, 2, 4, 6, 3

La prima cosa che dobbiamo fare è determinare le varianze di tutte le variabili:

In secondo luogo, troviamo la covarianza tra ciascuna coppia di variabili:

E una volta calcolate tutte le varianze e le covarianze, non resta che creare la matrice di covarianza. Per fare ciò, mettiamo i valori di varianza sulla diagonale principale della matrice e i valori di covarianza nella posizione corrispondente:

Come puoi vedere, rappresentando le varianze e le covarianze in una matrice, è molto semplice interpretare le variabili. La variabile con la maggiore dispersione è Y (23.44), invece le variabili X e Y hanno una relazione diretta, mentre le variabili X e Z (e quindi Y e Z) hanno una relazione inversa.

Si noti che la matrice di covarianza è sempre simmetrica, poiché la covarianza tra due variabili non dipende dall’ordine delle variabili. Per esempio,

è uguale a

Inoltre, la matrice di covarianza sarà sempre una matrice quadrata e la sua dimensione sarà uguale al numero di variabili. In questo caso avevamo tre variabili ed è per questo che è una matrice 3×3, ma se avessimo avuto solo due variabili la matrice di covarianza sarebbe stata 2×2.

Proprietà della matrice di covarianza

La matrice di covarianza ha le seguenti caratteristiche:

• La matrice di covarianza è una matrice quadrata dell’ordine del numero di variabili.
• La matrice di covarianza è simmetrica, il che significa che la diagonale principale della matrice è un asse di simmetria.
• La matrice di covarianza è sempre semidefinita positiva.
• Il determinante della matrice di covarianza è uguale o maggiore di zero.