Media aritmetica

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

Qui spieghiamo cos’è la media aritmetica e come viene calcolata. Troverai esempi di media aritmetica e persino una calcolatrice per trovare la media aritmetica di qualsiasi campione statistico. Infine potrai vedere quali sono le proprietà di questo tipo di media e come si ottiene la media aritmetica con i dati raggruppati in intervalli.

Qual è la media aritmetica?

La media aritmetica è un valore centrale caratteristico di un insieme di dati statistici. Per calcolare la media aritmetica, tutti i valori vengono sommati e divisi per il numero totale di dati.

Inoltre, la media aritmetica è uno dei principali indicatori utilizzati per effettuare uno studio statistico di un campione.

La formula della media aritmetica è quindi la seguente:

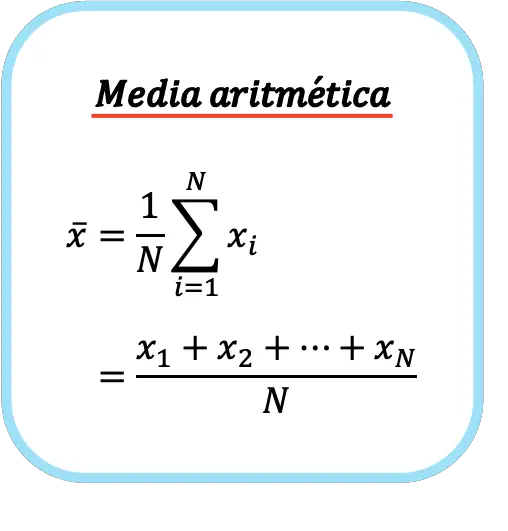
Il simbolo della media aritmetica è una fascia orizzontale sopra la lettera x.

$(\overline{x}).$

Puoi anche differenziare la media campionaria da quella della popolazione con il simbolo della media: la media di un campione è espressa con il simbolo

$\overline{x}$

, invece, per la media di una popolazione si usa la lettera greca

$\mu.$

Va notato che la media aritmetica di una popolazione equivale al valore atteso della variabile statistica.

La media aritmetica, detta anche media aritmetica, non è l’unico tipo di media esistente, esiste anche la media ponderata, la media quadrata, la media geometrica e la media armonica, tra le altre. Puoi vedere come viene calcolato ciascuno di essi nel motore di ricerca del nostro sito web.

Come calcolare la media aritmetica

Per calcolare la media aritmetica è necessario eseguire i seguenti passaggi:

Aggiungere tutti i dati statistici dal campione.
Dividere la somma precedente per il numero totale di dati.
Il risultato ottenuto è la media aritmetica del campione statistico.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la media aritmetica di qualsiasi set di dati.

Esempio di calcolo della media aritmetica

Data la definizione di media aritmetica, vedremo come ottenere la media aritmetica di un insieme di dati risolvendo passo dopo passo un esempio.

Uno studente ha conseguito nel corso di un anno scolastico i seguenti voti: in matematica un 9, in lingue un 7, in storia un 6, in economia un 8 e in scienze un 7,5. Qual è la media aritmetica di tutti i tuoi voti?

Per trovare la media aritmetica dobbiamo sommare tutti i voti e poi dividerli per il numero totale delle materie del corso, che è 5. Applichiamo quindi la formula della media aritmetica:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

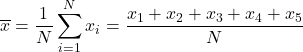
Sostituiamo i dati nella formula e calcoliamo la media aritmetica:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Come puoi vedere, nella media aritmetica, a ciascun valore viene assegnato lo stesso peso, cioè ogni dato ha lo stesso peso all’interno dell’insieme.

Calcolatore della media aritmetica

Inserisci i dati di qualsiasi campione statistico nella seguente calcolatrice per calcolarne la media aritmetica. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Media aritmetica per dati raggruppati

Per dati raggruppati intendiamo che i dati sono strutturati come gruppi o intervalli. Ciò di solito accade quando la dimensione del campione statistico è molto ampia.

Quindi il calcolo della media aritmetica varia leggermente quando i dati vengono raggruppati, anche se il concetto è lo stesso.

Per calcolare la media aritmetica dei dati raggruppati in intervalli, il punteggio della classe di ciascun gruppo deve essere moltiplicato per la sua frequenza assoluta e quindi diviso per la somma di tutte le frequenze assolute.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Nota: il punteggio della classe di un intervallo viene calcolato dividendo la somma dei punti finali dell’intervallo per due. Ad esempio, la nota di classe dell’intervallo [3,7) sarebbe:

$\cfrac{3+7}{2}=5$

Per poter vedere come si fa, di seguito è riportato un esercizio risolto sulla media aritmetica dei dati raggruppati in intervalli:

Vogliamo studiare statisticamente il peso di un gruppo, per questo abbiamo intervistato un gruppo rappresentativo di 81 persone e abbiamo ottenuto i seguenti dati:

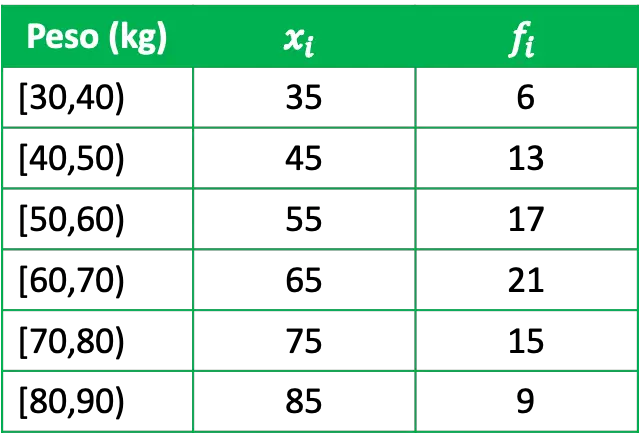
Dove x _i è il punteggio della classe di ciascun gruppo e f _i la sua frequenza assoluta, cioè il numero di persone che hanno un peso in questo intervallo.

Per determinare la media aritmetica è necessario aggiungere nella tabella delle frequenze una colonna che è il prodotto delle note della classe per le rispettive frequenze assolute:

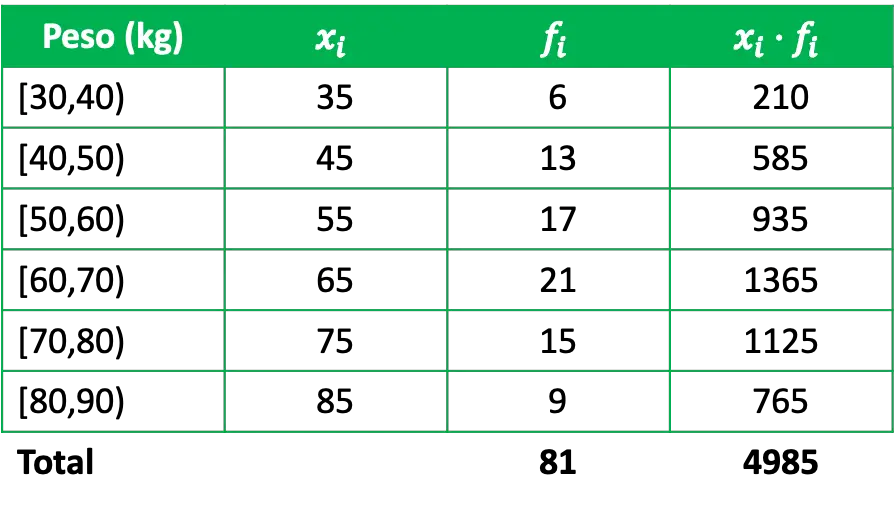
Esercizio sulla media aritmetica risolto per dati raggruppati

Pertanto, per calcolare la media aritmetica dei dati raggruppati, dividi semplicemente la somma dei prodotti delle note della classe per le loro frequenze per il numero totale di dati:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Proprietà della media aritmetica

La media aritmetica ha le seguenti caratteristiche:

La somma delle deviazioni di tutti i dati in una distribuzione dalla media dà come risultato zero.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Se aggiungiamo la stessa quantità a tutti i dati in un campione, la media del campione aumenta di quella quantità.

La stessa cosa accade con la moltiplicazione, se si moltiplicano tutti i valori di un campione per un numero, la media campionaria viene moltiplicata per quel numero.

La media aritmetica può essere calcolata solo in variabili quantitative . In altre parole, non è possibile fare la media delle variabili qualitative.

La media aritmetica sarà sempre un valore compreso tra il minimo e il massimo di una distribuzione.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Questo tipo di media è molto sensibile a valori molto alti o molto bassi, facendo sì che un valore anomalo modifichi significativamente il risultato della media aritmetica.

La media aritmetica di un set di dati è sempre uguale o maggiore della media geometrica dello stesso set di dati.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Calcola la media aritmetica con Excel

Calcolare la media aritmetica in Excel è molto semplice, poiché basta inserire i dati su un foglio e utilizzare la funzione MEDIA .

Ad esempio, per determinare la media aritmetica dei dati del primo esercizio risolto che abbiamo spiegato, è sufficiente copiare tutti i dati in un documento Excel e scrivere in una cella la seguente formula: =MEDIA(9;7;5; 8;7 ,5) . La funzione restituirà la media aritmetica dei dati, che è 7,3.

Ovviamente è molto più veloce trovare la media aritmetica di certi numeri con il programma Excel che calcolarla a mano, soprattutto quando la dimensione del campione è molto ampia.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più