Media armonica

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

Qui spieghiamo cos’è la media armonica e come viene calcolata (formula). Inoltre, calcoliamo passo dopo passo la media armonica di un esempio. Troverai anche una calcolatrice per calcolare la media armonica di qualsiasi set di dati. E infine potrai vedere quali sono le proprietà della media armonica.

Qual è la media armonica?

La media armonica è una misura di posizione centrale della statistica descrittiva. La media armonica viene calcolata dividendo il numero totale di dati statistici per la somma dei reciproci di ciascun valore.

La media armonica viene utilizzata per calcolare velocità medie, tempi o effettuare calcoli elettronici. Questa caratteristica differenzia la media armonica da altri tipi di medie, frequentemente utilizzate nel calcolo dei prezzi medi o delle percentuali.

Quindi, la formula per la media armonica è la seguente:

La media armonica è solitamente rappresentata da una H maiuscola.

Altri tipi di media esistenti sono la media aritmetica, la media ponderata, la media quadrata e la media geometrica. La media armonica presenta vantaggi e svantaggi rispetto ad altri tipi di media, di seguito vedremo quali sono.

Come calcolare la media armonica

Per calcolare la media armonica è necessario eseguire i seguenti passaggi:

Calcolare l’inverso di ciascun dato statistico nel campione.
Aggiungi tutti gli inversi calcolati.
Dividere il numero totale di dati per la somma trovata nel passaggio precedente.
Il risultato ottenuto è la media armonica del campione statistico.

👉 Come puoi vedere, calcolare la media armonica di un insieme di dati richiede molte operazioni, quindi è piuttosto laborioso farlo a mano. Pertanto, per calcolare la media armonica, si consiglia di utilizzare il calcolatore riportato di seguito.

Esempio di media armonica

Dopo aver visto la teoria sulla media armonica, vedremo come trovare la media armonica di un insieme di dati risolvendo un esempio passo passo del prezzo di un’azione.

Una persona acquista azioni di una società ogni anno per 5 anni consecutivi. Durante questo periodo il prezzo delle azioni oscillò molto: nel primo anno ogni azione valeva 7 euro, nel secondo anno 10 euro, nel terzo anno 15 euro, nel quarto anno la società subì notevoli perdite finanziarie e la il prezzo scese a 6 euro per azione e alla fine, nel quinto anno, la società fece un grande investimento che fece aumentare il prezzo a 11 euro. Qual è stato il prezzo medio di acquisto delle azioni?

Una possibilità potrebbe essere quella di calcolare la media aritmetica, cioè sommare tutti i prezzi e dividerli per cinque. Tuttavia, poiché gli acquisti sono stati effettuati in anni diversi, fare la media aritmetica sarebbe un errore. Dobbiamo quindi trovare la media armonica di tutti i prezzi.

Successivamente applichiamo la formula della media armonica:

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+\frac{1}{x_4}+\frac{1}{x_5}}$

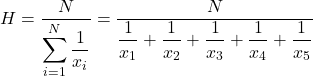
E poi sostituiamo i valori dei prezzi problematici nella formula e calcoliamo la media armonica:

$\displaystyle H=\frac{5}{\displaystyle\frac{1}{7}+\frac{1}{10}+\frac{1}{15}+\frac{1}{6}+\frac{1}{11}}=8,82$

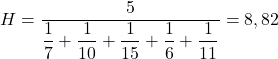
Devi mettere cinque al numeratore della frazione perché ci sono cinque informazioni diverse.

Pertanto, il prezzo medio delle azioni acquistate durante questo periodo è di 8,82 euro per azione.

Calcolatore della media armonica

Con il seguente calcolatore puoi calcolare la media armonica di qualsiasi set di dati statistici.

È necessario inserire i numeri utilizzando il punto come separatore decimale e separarli con uno spazio. Ricorda che per trovare la media armonica, nessun valore può essere zero.

Proprietà della media armonica

La media armonica ha le seguenti caratteristiche:

Valori grandi hanno poco effetto sulla media armonica di un insieme, cioè un valore molto grande rispetto ad altri dati non causerà un cambiamento notevole nella media armonica.

D’altra parte, un valore piccolo influenza notevolmente la media armonica di un insieme, riducendone notevolmente il valore. Infatti, i reciproci del denominatore della formula assumono quindi valori molto grandi.

La media armonica non può essere calcolata se uno qualsiasi dei dati è zero, poiché ciò causerebbe indeterminatezza nella formula. In tal caso si dice che la media armonica è indefinita.

Il reciproco della media armonica è equivalente alla media aritmetica dei reciproci delle osservazioni.

Per lo stesso gruppo di dati, la media armonica sarà inferiore o uguale alla media aritmetica.

$\cfrac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}\leq \cfrac{x_1+x_2+\dots+x_N}{N}$

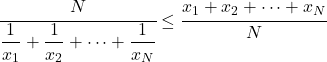
Calcola la media armonica con Excel

Come abbiamo visto, calcolare manualmente la media armonica può essere piuttosto noioso perché è necessario eseguire molti calcoli. E diventa ancora più complicato quando si hanno a disposizione grandi quantità di dati. Pertanto, per trovare la media armonica, si consiglia di utilizzare una calcolatrice o il programma Excel.

La media armonica in Excel si calcola con la formula MEDIA.ARMO . Cioè, per calcolare la media armonica di un insieme di dati, è necessario copiarli in un foglio Excel e inserire tutti i dati nella funzione MEDIA.ARMO .

Ad esempio, per ottenere la media armonica dell’esercizio che abbiamo risolto sopra, scrivi in una cella di Excel =MEDIA.ARMO(7;10;15;6;11) .

Dovresti tenere presente che se uno qualsiasi dei valori è zero, la funzione restituirà un errore, perché la media armonica di un insieme di valori statistici non può essere determinata se uno di essi è zero.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più