Come trovare la media e la deviazione standard dei dati raggruppati

Spesso vogliamo calcolare la media e la deviazione standard dei dati raggruppati in qualche modo. Ad esempio, supponiamo di avere i seguenti dati raggruppati:

Sebbene non sia possibile calcolare la media esatta e la deviazione standard poiché non conosciamo i valori dei dati grezzi , è possibile stimare la media e la deviazione standard.

I passaggi seguenti spiegano come eseguire questa operazione.

Correlato: Come trovare la modalità dati raggruppati

Calcolare la media dei dati raggruppati

Possiamo utilizzare la seguente formula per stimare la media dei dati raggruppati:

Media: Σm _i n _i / N

Oro:

• _mi : La metà ^{dell’iesimo} gruppo
• n _i : La frequenza ^{dell’iesimo} gruppo
• N: la dimensione totale del campione

Ecco come applicheremmo questa formula al nostro set di dati precedente:

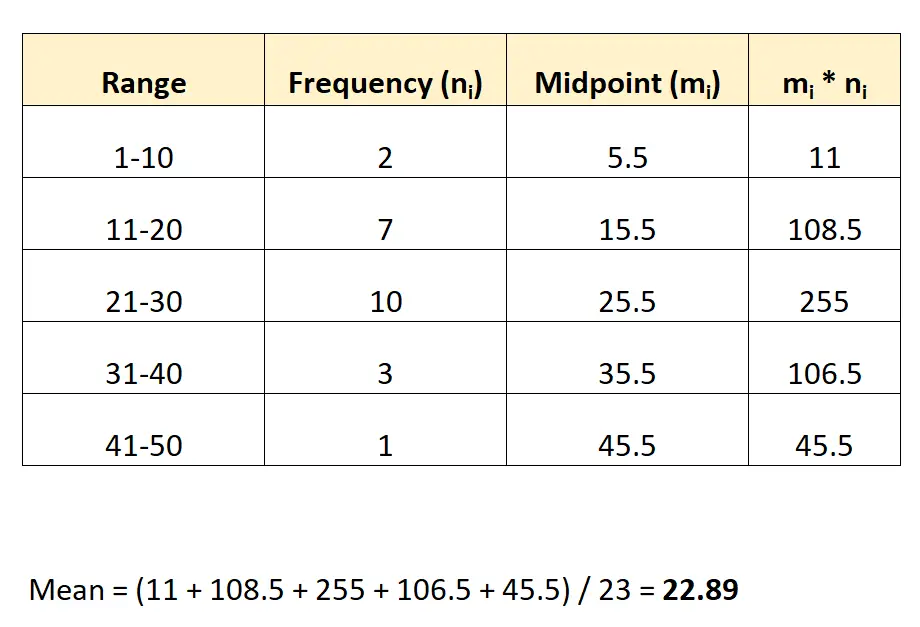
La media del set di dati risulta essere 22,89 .

Nota: il punto medio di ciascun gruppo può essere trovato prendendo la media dei valori inferiore e superiore dell’intervallo. Ad esempio, il punto medio del primo gruppo viene calcolato come segue: (1+10) / 2 = 5,5.

Calcolare la deviazione standard dei dati raggruppati

Possiamo utilizzare la seguente formula per stimare la deviazione standard dei dati raggruppati:

Deviazione standard: √ Σn _i (m _i -μ) ² / (N-1)

Oro:

• n _i : La frequenza ^{dell’iesimo} gruppo
• _mi : La metà ^{dell’iesimo} gruppo
• μ : La media
• N: la dimensione totale del campione

Ecco come applicheremmo questa formula al nostro set di dati:

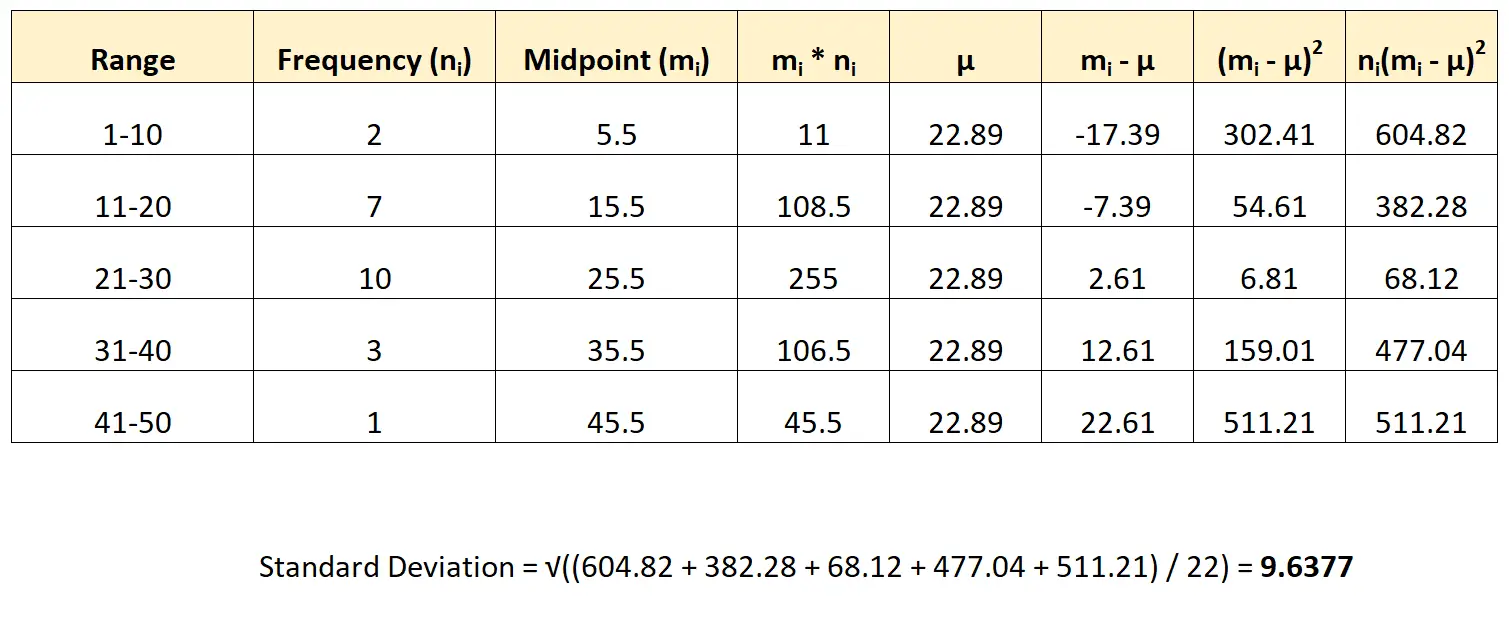La deviazione standard del set di dati risulta essere 9.6377 .

Risorse addizionali

Come stimare la media e la mediana di qualsiasi istogramma
Come calcolare la classificazione percentile per i dati raggruppati
Come trovare la mediana dei dati raggruppati