Come calcolare la media dalla tabella delle frequenze (con esempi)

Puoi calcolare la media di una tabella di frequenza utilizzando la seguente formula:

Media = Σfx / Σf

Oro:

• Σ : un simbolo di fantasia che significa “somma”
• f : la frequenza di un particolare valore
• x : il valore nella tabella delle frequenze

Gli esempi seguenti mostrano come utilizzare questa formula nella pratica.

Esempio 1: numero medio di vincite

La seguente tabella di frequenza mostra il numero totale di vittorie per 30 squadre di calcio in un dato campionato:

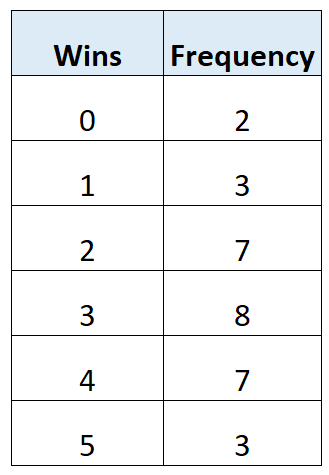
Possiamo utilizzare la seguente formula per calcolare il numero medio di vincite:

• Media = (0*2 + 1*3 + 2*7 + 3*8 + 4*7 + 5*3) / (2 + 3 + 7 + 8 + 7 + 3)
• Media = (0 + 3 + 14 + 24 + 28 + 15) / (30)
• Media = (84) / (30)
• Media = 2,8

Il numero medio di vittorie è 2,8 .

Esempio 2: numero medio di animali domestici

La seguente tabella di frequenza mostra il numero totale di animali appartenenti a 20 famiglie diverse in un determinato quartiere:

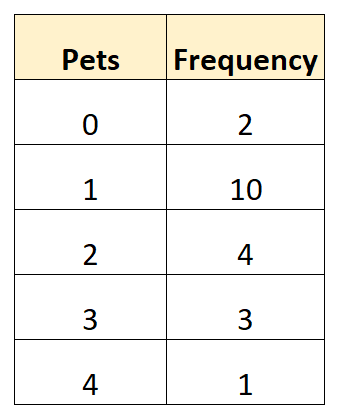
Possiamo utilizzare la seguente formula per calcolare il numero medio di animali posseduti:

• Media = (0*2 + 1*10 + 2*4 + 3*3 + 4*1) / (2 + 10 + 4 + 3 + 1)
• Media = (0 + 10 + 8 + 9 + 4) / (20)
• Media = (31) / (20)
• Media = 1,55

Il numero medio di animali domestici posseduti è di 1,55 .

Esempio 3: dimensione media della famiglia

La seguente tabella di frequenza mostra le dimensioni delle famiglie di 40 famiglie diverse in una particolare area:

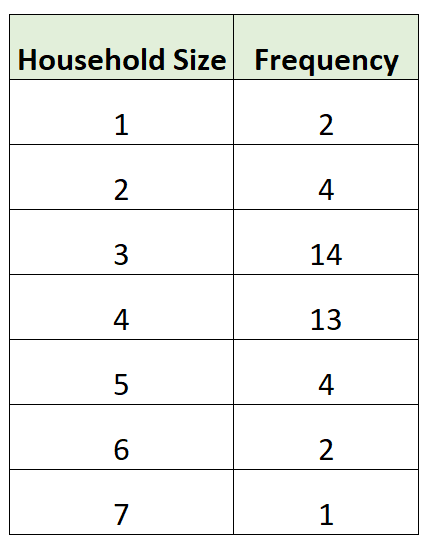
Possiamo utilizzare la seguente formula per calcolare la dimensione media della famiglia:

• Media = (1*2 + 2*4 + 3*14 + 4*13 + 5*4 + 6*2 + 7*1) / (2 + 4 + 14 + 13 + 4 + 2+1)
• Media = (2 + 8 + 42 + 52 + 20 + 12 + 7) / (40)
• Media = (143) / (40)
• Media = 3.575

La dimensione media del nucleo familiare è di 3.575 persone .

Risorse addizionali

Come calcolare la mediana dalla tabella delle frequenze
Come calcolare la modalità dalla tabella delle frequenze
Come trovare la media, la mediana e la moda nei grafici di fusti e foglie
Come stimare la media e la mediana degli istogrammi
Quando utilizzare la media rispetto alla mediana