Mezzi geometrici

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

In questo articolo spieghiamo cos’è la media geometrica, come si calcola e qual è la differenza tra media geometrica e media aritmetica. Potrai anche vedere un esercizio risolto passo dopo passo della media geometrica e quali sono le proprietà di questo tipo di media. Infine, troverai una calcolatrice per calcolare la media geometrica di qualsiasi set di dati.

Qual è la media geometrica?

La media geometrica è una misura della centralità della statistica descrittiva. La media geometrica di un insieme di dati statistici è uguale alla radice n-esima del prodotto di tutti i valori.

La media geometrica viene utilizzata nella finanza aziendale per calcolare i tassi di rendimento, le medie percentuali e gli interessi composti.

La formula della media geometrica è quindi la seguente:

La media geometrica può essere calcolata solo quando tutti i dati nel campione sono positivi. Perché se un valore fosse negativo la radice avrebbe soluzione negativa o nessuna soluzione, invece se un dato fosse zero allora la moltiplicazione dei dati darebbe zero e quindi la media geometrica sarebbe pari a 0.

La media geometrica non è l’unico tipo di media esistente, esiste anche la media aritmetica, la media ponderata, la media quadrata e la media armonica.

Differenza tra media geometrica e media aritmetica

La differenza principale tra la media geometrica e la media aritmetica è che la media geometrica è meno sensibile ai valori estremi rispetto alla media aritmetica. Inoltre, la media aritmetica può essere calcolata con valori negativi e zero, mentre la media geometrica può essere calcolata solo con valori positivi.

Allo stesso modo, la media geometrica sarà generalmente inferiore alla media aritmetica per lo stesso set di dati.

Va inoltre notato che il calcolo della media geometrica è più complesso e quindi la sua significatività statistica è più difficile da interpretare.

Insomma, la media geometrica presenta vantaggi e svantaggi rispetto alla media aritmetica e, a seconda della natura dei dati, sarà opportuno calcolare questa o quella media.

Come calcolare la media geometrica

Per calcolare la media geometrica è necessario eseguire i seguenti passaggi:

Calcolare il prodotto di tutti i dati statistici nel campione.
Trova la radice ennesima del prodotto calcolato.
Il risultato ottenuto è la media geometrica del campione statistico.

Come puoi vedere, trovare la media geometrica di un insieme di dati è relativamente semplice con una calcolatrice o un programma per computer, poiché devi solo calcolare un prodotto e una radice. Al contrario, è piuttosto laborioso eseguire il calcolo a mano.

👉 Ecco perché ti consigliamo di utilizzare la calcolatrice qui sotto per calcolare la media geometrica di un set di dati.

Esempio di media geometrica

Una volta che abbiamo visto la teoria sulla media geometrica, faremo un esempio in modo che tu possa vedere esattamente come ottenere la media geometrica.

I risultati economici di un’azienda negli ultimi cinque anni sono noti. Nel primo anno l’azienda ha generato una redditività economica del 10%, nel secondo anno il profitto ha raggiunto il 23%, nel terzo anno i soldi guadagnati sono stati del 16%, nel quarto anno ha raggiunto una redditività economica del 7% e l’investimento nel quinto anno ha rappresentato un rendimento del 20%. Ti viene chiesto di calcolare la media di tutte le percentuali.

Come abbiamo visto, per calcolare la media delle percentuali non bisogna utilizzare la media aritmetica, ma piuttosto fare il calcolo con la media geometrica.

Applichiamo quindi la formula della media geometrica:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

E sostituiamo i valori di esempio nella formula ed eseguiamo il calcolo:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Nota che abbiamo cinque punti dati, quindi stiamo calcolando la quinta radice.

Il risultato numerico della media geometrica è 1,15, il che significa che l’azienda ha registrato una crescita economica media del 15% ogni anno.

Tieni presente che siamo riusciti a ottenere la media geometrica perché tutti i valori erano positivi, ma se qualche percentuale fosse stata negativa avremmo dovuto inserire i dati nella formula come decimale positivo con la parte intera. uguale a zero. Ad esempio, una crescita del -30% dovrebbe essere espressa nella formula come 0,70 (1-0,3=0,7).

Calcolatore della media geometrica

Inserisci qualsiasi statistica campione nel calcolatore sottostante per trovare la sua media geometrica. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale. Ricorda che non puoi determinare la media geometrica se un valore è negativo o zero.

Proprietà della media geometrica

La media geometrica ha le seguenti caratteristiche:

Questo è un tipo di media molto utile per trovare la media di percentuali o indici.

Può essere calcolato solo se tutti i dati sono positivi.

Il significato geometrico della media geometrica di due numeri aeb è il lato di un quadrato avente la stessa area del rettangolo i cui lati misurano aeb .

$MG(a,b)=\sqrt{a\cdot b}$

Il significato geometrico della media geometrica di tre numeri a , b e c è il lato di un cubo il cui volume è equivalente al parallelepipedo di lati a , b e c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Il logaritmo della media geometrica di un insieme di dati dà la media aritmetica dei logaritmi dello stesso insieme.

La media geometrica di un insieme di valori sarà sempre inferiore o uguale alla media aritmetica.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

La media geometrica ponderata viene calcolata allo stesso modo della media geometrica, ma aggiungendo pesi all’esponente di ciascun dato per ponderare i valori statistici.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

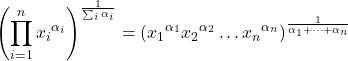
Calcola la media geometrica in Excel

Infine, vediamo come trovare la media geometrica di un set di dati utilizzando il programma Excel.

Per calcolare la media geometrica in Excel, è necessario utilizzare la funzione MEDIA.GEOM. Inserisci semplicemente tutti i valori di cui vuoi prendere la media geometrica e la funzione restituirà il risultato della media geometrica.

Ad esempio, per determinare la media geometrica dell’esempio lavorato sopra, è necessario scrivere in una casella Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Tieni presente che se uno qualsiasi dei valori è zero o negativo, la funzione restituirà un errore.

Come puoi vedere, è molto più semplice e veloce calcolare una media geometrica con Excel, poiché basta copiare i dati su un foglio e utilizzare una formula.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più