Media ponderata

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

Qui spieghiamo cos’è la media ponderata e come viene calcolata. Potrai vedere un esercizio risolto su come troviamo la media ponderata. Inoltre, puoi calcolare la media ponderata di qualsiasi set di dati con la calcolatrice alla fine.

Qual è la media ponderata?

La media ponderata è una misura della centralità delle statistiche descrittive. Per calcolare la media ponderata, è necessario prima moltiplicare ciascun dato statistico per il suo peso (o peso), quindi sommare tutti i prodotti e infine dividere la somma ponderata per la somma di tutti i pesi.

In altre parole, la formula per la media ponderata è la seguente:

Dove x _i rappresenta ciascun campione di dati e w _i il suo peso corrispondente.

Pertanto, maggiore è il peso di un dato, maggiore è la sua importanza nel calcolo della media ponderata. In altre parole, quanto maggiore è la ponderazione di un dato, tanto più influenzerà il risultato della media ponderata.

La media ponderata è particolarmente utile per il calcolo dei voti, perché permette di valutare con diversa importanza gli esercizi o gli esami sostenuti durante un corso. La media ponderata viene utilizzata anche per calcolare il CPI (indice dei prezzi al consumo), che è un indicatore per misurare i prezzi di una popolazione.

Oltre alla media ponderata, esistono anche altri tipi di media come la media geometrica, la media aritmetica, la media quadrata e la media armonica.

Come calcolare la media ponderata

Per calcolare la media ponderata è necessario seguire i seguenti passaggi:

Moltiplicare ciascun dato statistico per il suo peso corrispondente.
Somma tutti i prodotti calcolati nel passaggio precedente.
Dividere la somma ponderata sopra per la somma di tutti i pesi.
Il risultato ottenuto è la media ponderata del campione statistico.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la media ponderata di qualsiasi set di dati.

Esempio di media ponderata

Considerando la definizione di media ponderata, risolveremo ora un esercizio per comprendere appieno come si ottiene la media ponderata da un insieme di dati.

Uno studente del 1° anno delle superiori ha ottenuto nella materia di matematica i seguenti voti: un 7 nella prova parziale che vale il 30%, un 9 nel lavoro di gruppo che vale il 20%, un 6 negli esercizi dati in classe con ponderazione del 10% e un 8 all’esame finale che ha un peso del 40%. Qual è il tuo voto finale per la materia?

Per determinare il voto dello studente è necessario individuare la media ponderata con i valori indicati nel prospetto. Per fare ciò applichiamo la formula della media ponderata:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

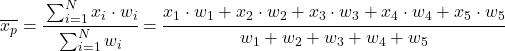
Il punteggio di ciascun deliverable costituisce il valore statistico e la sua percentuale corrisponde al peso di detto valore. Pertanto, sostituiamo i valori e i pesi nella formula ed eseguiamo il calcolo della media ponderata:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Il voto finale di matematica di questo studente sarà quindi 7,7 perché questo è il risultato ottenuto dalla media ponderata.

Calcolatore della media ponderata

Inserisci i dati di qualsiasi campione statistico e i rispettivi pesi nel calcolatore sottostante per calcolare la sua media ponderata.

Inserisci i dati statistici nella prima casella e i rispettivi pesi nella seconda casella. È necessario scrivere i pesi nello stesso ordine dei dati e in formato decimale. Tutti i numeri devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Pesi standardizzati

Come abbiamo visto, nella media ponderata, il peso è il valore che viene dato a ciascun dato per dargli più o meno importanza. Quindi, se l’informazione è molto importante, avrà un peso molto elevato, ma se l’informazione non è molto rilevante, avrà un peso molto basso.

Ebbene, il peso normalizzato è un tipo di ponderazione utilizzata per ottenere la media ponderata senza dover effettuare alcuna divisione.

Il peso normalizzato è il peso di un elemento dati diviso per la somma di tutti i pesi.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

La somma di tutti i pesi normalizzati è quindi uguale a uno:

$\sum_{i=1}^N w_i'=1$

Quindi, per calcolare la media ponderata con i pesi normalizzati , è sufficiente moltiplicare ciascun dato per il suo peso normalizzato:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

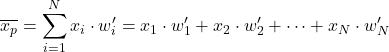
Ad esempio, abbiamo un campione statistico i cui dati sono 24, 35, 17, 41 e i rispettivi pesi sono 4, 9, 6, 3. Per trovare la media ponderata di questo set di dati, possiamo prima calcolare i pesi normalizzati dividendo ciascun peso per la somma di tutti i pesi:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

E ora basta moltiplicare ciascun dato per il suo peso normalizzato e il risultato sarà la media ponderata:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Differenza tra media ponderata e media aritmetica

Il calcolo della media ponderata e della media aritmetica si effettua allo stesso modo, poiché occorre eseguire operazioni simili. Nella media ponderata, ciascun punto dati viene moltiplicato per il suo peso e diviso per la somma dei pesi, ma nella media aritmetica tutti i dati vengono sommati e divisi per il numero totale di punti dati.

La differenza tra la media ponderata e la media aritmetica sta nel suo concetto, poiché nella media aritmetica si considera che tutti i dati abbiano lo stesso valore, tuttavia nella media ponderata ogni dato ha un peso diverso.

Si noti che se tutti i pesi sono uguali, la media ponderata è equivalente alla media aritmetica. Puoi vedere la dimostrazione matematica qui sotto:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più