Come trovare la mediana dei dati raggruppati: con esempi

Spesso vogliamo calcolare la mediana dei dati raggruppati in qualche modo.

Ricordiamo che la mediana rappresenta il valore che si trova direttamente al centro di un set di dati, quando tutti i valori sono ordinati dal più piccolo al più grande.

Ad esempio, supponiamo di avere i seguenti dati raggruppati:

Sebbene non sia possibile calcolare la mediana esatta poiché non conosciamo i valori dei dati grezzi , è possibile stimare la mediana utilizzando la seguente formula:

Mediana dei dati raggruppati = L + W[(N/2 – C) / F]

Oro:

• L : Limite inferiore della classe mediana
• W : Ampiezza media della classe
• N : Frequenza totale
• C : Frequenza cumulativa fino alla classe mediana
• F : Frequenza mediana della classe

Nota : la classe media è la classe che contiene il valore situato in N/2. Nell’esempio sopra, ci sono N = 23 valori totali. Pertanto, il valore mediano è quello nella posizione 23/2 = 11,5, che sarebbe nella classe 21-30.

Gli esempi seguenti mostrano come calcolare la mediana dei dati raggruppati in diversi scenari.

Esempio 1: calcolare la mediana dei dati raggruppati

Supponiamo di avere la seguente distribuzione di frequenza che mostra l’esame valutato da 40 studenti in una determinata classe:

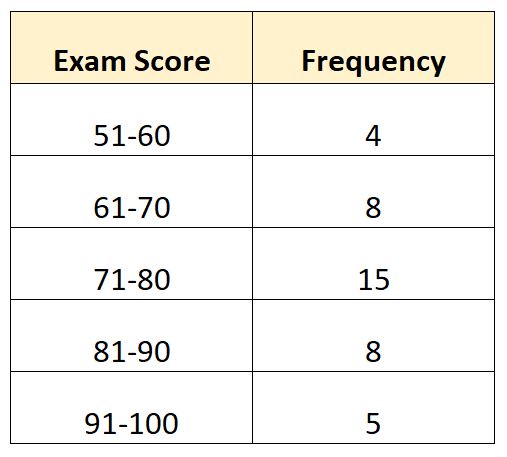
In questo esempio, ci sono N = 40 valori totali. Quindi il valore mediano è nella classe in cui si trova 40/2 = 20. Il ventesimo valore più grande sarebbe nella classe 71-80 .

Sapendo questo possiamo calcolare i seguenti valori:

• L : Limite della classe medio-bassa: 71
• W : Ampiezza media della classe: 9
• N : Frequenza totale: 40
• C : Frequenza cumulativa fino alla classe media: 12
• F : Frequenza media delle lezioni: 15

Possiamo inserire questi valori nella formula per calcolare la mediana della distribuzione:

• Mediana = L + W[(N/2 – C) / F]
• Mediana = 71 + 9[(40/2 – 12) / 15]
• Mediana = 75,8

Stimiamo che il punteggio medio dell’esame sia 75,8 .

Esempio 2: calcolare la mediana dei dati raggruppati

Supponiamo di avere la seguente distribuzione di frequenza che mostra il numero di punti segnati per partita da 60 giocatori di basket:

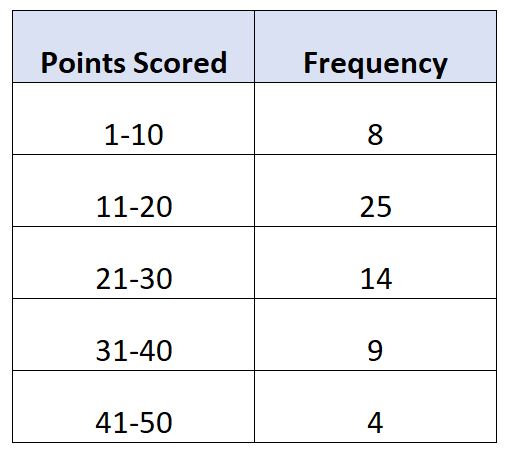
In questo esempio, ci sono N = 60 valori totali. Pertanto, il valore mediano si trova nella classe in cui si trova 60/2 = 30. Il trentesimo valore più grande sarebbe nella classe 11-20 .

Sapendo questo possiamo calcolare i seguenti valori:

• L : Limite della classe medio-bassa: 11
• W : Ampiezza media della classe: 9
• N : Frequenza totale: 60
• C : Frequenza cumulativa fino alla classe mediana: 8
• F : Frequenza media delle lezioni: 25

Possiamo inserire questi valori nella formula per calcolare la mediana della distribuzione:

• Mediana = L + W[(N/2 – C) / F]
• Mediana = 11 + 9[(60/2 – 8) / 25]
• Mediana = 18,92

Stimiamo che il punteggio medio dell’esame sia 18,92 .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre operazioni comuni con dati raggruppati:

Come trovare la media e la deviazione standard dei dati raggruppati
Come trovare la modalità dati raggruppati
Come calcolare la classificazione percentile per i dati raggruppati