Come calcolare la mediana dalla tabella delle frequenze (con esempi)

Puoi trovare il valore mediano di una tabella di frequenza procedendo come segue:

Passaggio 1: disporre tutti i valori individuali dal più piccolo al più grande.

Passaggio 2: identifica il valore direttamente al centro dell’elenco ordinato.

• Se è presente un numero dispari di valori, la mediana è il valore direttamente al centro.
• Se il numero di valori è pari, la mediana è la media dei due valori medi.

Gli esempi seguenti mostrano come trovare nella pratica il valore mediano di una tabella di frequenza.

Esempio 1: mediana della tabella delle frequenze (numero dispari di valori)

La seguente tabella di frequenza mostra il numero totale di vittorie di 17 squadre di calcio in un dato campionato:

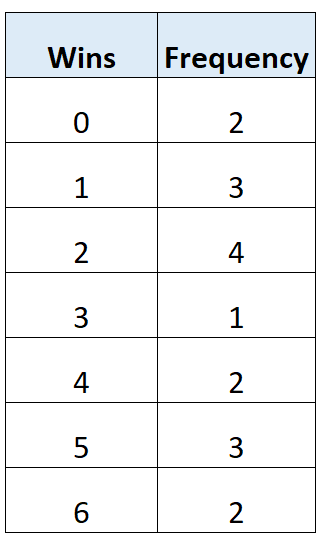
Possiamo utilizzare i seguenti passaggi per trovare il valore mediano in questa tabella di frequenza:

Passaggio 1: disporre tutti i valori individuali dal più piccolo al più grande.

Valori: 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 5, 6, 6

Passaggio 2: identifica il valore direttamente al centro dell’elenco ordinato.

Valori: 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 4 , 4, 5, 5, 5, 6, 6

Il valore medio è 2 .

Esempio 2: mediana della tabella delle frequenze (numero pari di valori)

La seguente tabella di frequenza mostra le dimensioni delle famiglie di 20 famiglie diverse in una particolare area:

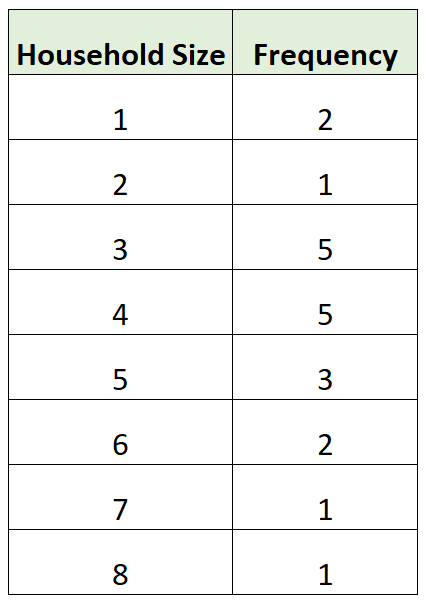
Possiamo utilizzare i seguenti passaggi per trovare il valore mediano in questa tabella di frequenza:

Passaggio 1: disporre tutti i valori individuali dal più piccolo al più grande.

Valori: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8

Passaggio 2: identifica il valore direttamente al centro dell’elenco ordinato.

Valori: 1, 1, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4 , 4, 5 , 5 , 5, 6, 6, 7, 8

Ci sono due valori posizionati direttamente al centro: 4 e 4.

Quindi, il valore mediano è la media di questi due valori: (4 + 4) / 2 = 4 .

Risorse addizionali

Come calcolare la media dalla tabella delle frequenze
Come calcolare la modalità dalla tabella delle frequenze
Come stimare la media e la mediana degli istogrammi
Quando utilizzare la media rispetto alla mediana