Mediano

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la mediana di un set di dati e come trovare la mediana per i dati non raggruppati e i dati raggruppati. Inoltre, puoi calcolare la mediana di qualsiasi serie di dati con il calcolatore online alla fine.

Qual è la mediana?

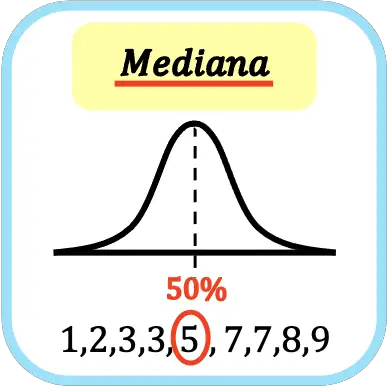
Nelle statistiche, la mediana è il valore medio di tutti i dati ordinati dal più piccolo al più grande. In altre parole, la mediana divide il set di dati ordinato in due parti uguali.

La mediana è una misura della posizione centrale utilizzata per descrivere una distribuzione di probabilità.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la mediana di qualsiasi set di dati.

In generale, il termine Sé è spesso usato come simbolo del centro.

Altre misure di posizione centrale sono la media e la moda, di seguito vedremo le differenze tra loro. Allo stesso modo, le misure della posizione non centrale sono quartili, quintili, decili, percentili, ecc.

Va notato che la mediana di un set di dati coincide con il secondo quartile, il quinto decile e il 50° percentile.

Come calcolare la mediana

Il calcolo della mediana dipende dal fatto che il numero totale di dati sia pari o dispari:

Se il numero totale di dati è dispari , la mediana sarà il valore che si trova proprio al centro dei dati. Vale a dire il valore che si trova nella posizione (n+1)/2 dei dati ordinati.

$Me=x_{\frac{n+1}{2}$

Se il numero totale di punti dati è pari , la mediana sarà la media dei due punti dati situati al centro. Vale a dire la media aritmetica dei valori che si trovano alle posizioni n/2 e n/2+1 dei dati ordinati.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Oro

$n$

è il numero totale di elementi di dati nel campione.

Esempi di calcolo della mediana

Per poter vedere come viene calcolata la mediana, di seguito sono riportati due esempi reali, uno per ciascun caso. Innanzitutto verrà calcolata la mediana di un set di dati dispari, quindi la mediana di un set di dati pari.

Mediana dei dati dispari

Calcola la mediana dei seguenti dati: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

La prima cosa che dobbiamo fare prima di eseguire i calcoli è ordinare i dati, ovvero inserire i numeri dal più piccolo al più grande.

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

In questo caso abbiamo 11 osservazioni, quindi il numero totale di dati è dispari. Pertanto, applichiamo la seguente formula per calcolare la posizione della mediana:

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

La mediana sarà quindi il dato situato in sesta posizione, che in questo caso corrisponde al valore 4.

$Me=x_6=4$

mediana dei dati pari

Qual è la mediana delle seguenti osservazioni? 2, 6, 2, 8, 9, 4, 7, 11, 4, 13

Per ottenere la mediana è necessario prima ordinare tutti i dati in ordine crescente:

$2 \ 2 \ 4 \ 4 \ 6 \ 7 \ 8 \ 9 \ 11 \ 13$

Questo esempio è diverso dal precedente, poiché questa volta abbiamo un totale di 10 osservazioni, che è un numero pari. Pertanto, la procedura per determinare la media è un po’ più complicata.

Devi prima calcolare le due posizioni centrali tra le quali verrà trovata la mediana, per questo devi applicare le due formule seguenti:

$\cfrac{n}{2}=\cfrac{10}{2}=5$

$\cfrac{n}{2}+1=\cfrac{10}{2}+1=6$

La mediana sarà quindi compresa tra la quinta e la sesta posizione, che corrispondono rispettivamente ai valori 6 e 7. Concretamente la mediana sarà la media aritmetica di detti valori:

$Me=\cfrac{x_5+x_6}{2}=\cfrac{6+7}{2}=6,5$

calcolatore della mediana

Inserisci un set di dati statistici nella seguente calcolatrice per calcolarne la mediana. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Mediana per dati raggruppati

Per calcolare la mediana quando i dati vengono raggruppati in intervalli, è necessario innanzitutto trovare l’intervallo o il contenitore in cui rientra la mediana utilizzando la seguente formula:

$\cfrac{n+1}{2}$

Pertanto, la mediana si troverà nell’intervallo la cui frequenza assoluta cumulativa è immediatamente maggiore del numero ottenuto con la precedente espressione algebrica.

E una volta conosciuto l’intervallo a cui appartiene la mediana, dobbiamo applicare la seguente formula per trovare il valore esatto della mediana:

$Me=L_i+ \cfrac{\displaystyle\frac{n+1}{2}-F_{i-1}}{f_i}\cdot I_i$

Oro:

L _i è il limite inferiore dell’intervallo in cui si trova la mediana.
n è il numero totale di osservazioni.
F _i-1 è la frequenza assoluta accumulata dell’intervallo precedente.
f _i è la frequenza assoluta dell’intervallo in cui si trova la mediana.
I _i è la larghezza dell’intervallo medio.

Ad esempio, di seguito hai risolto un esercizio in cui viene calcolata la mediana dei dati raggruppati in intervalli.

Per trovare la mediana del set di dati, dobbiamo prima determinare l’intervallo in cui rientra. Per fare ciò, utilizziamo la seguente formula:

$\cfrac{n+1}{2}=\cfrac{30+1}{2} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Quindi la mediana sarà nell’intervallo la cui frequenza assoluta cumulativa è immediatamente maggiore di 15,5, che in questo caso è l’intervallo [60,70) la cui frequenza assoluta cumulativa è 26. E una volta conosciuto l’intervallo mediano, applichiamo la seconda formula della processi:

$Me=L_i+ \cfrac{\displaystyle\frac{n+1}{2}-F_{i-1}}{f_i}\cdot I_i$

$Me=60+\cfrac{\displaystyle\frac{30+1}{2}-15}{11}\cdot 10=60,45$

In definitiva, la mediana del set di dati raggruppati è 60,45. Come puoi vedere, in questi tipi di problemi la mediana è solitamente un numero decimale.

mediana, media e moda

In quest’ultima sezione vedremo qual è la differenza tra mediana, media e moda. Ebbene, queste sono tre misure statistiche di posizione centrale ma il loro significato è diverso.

Come abbiamo visto, la mediana è definita come il valore che occupa la posizione centrale quando i dati vengono ordinati.

Al contrario, la media è il valore medio di tutti i dati statistici. Per calcolare la media, è necessario sommare tutti i dati e quindi dividere il risultato per il numero di punti dati.

Infine, la moda è il valore più ripetuto in una serie di dati.

Come puoi vedere, tutte e tre le misure statistiche aiutano a descrivere una distribuzione di probabilità, poiché forniscono un’idea dei suoi valori centrali. Tuttavia nessuna misura è migliore di un’altra, si riferiscono semplicemente a concetti diversi.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più