Come utilizzare il metodo dei minimi quadrati in r

Il metodo dei minimi quadrati è un metodo che possiamo utilizzare per trovare la retta di regressione che meglio si adatta a un dato insieme di dati.

Per utilizzare il metodo dei minimi quadrati per adattare una retta di regressione in R, possiamo utilizzare la funzione lm() .

Questa funzione utilizza la seguente sintassi di base:

 model <- lm(response ~ predictor, data=df)

L’esempio seguente mostra come utilizzare questa funzione in R.

Esempio: metodo dei minimi quadrati in R

Supponiamo di avere il seguente frame di dati in R che mostra il numero di ore studiate e il corrispondente punteggio dell’esame per 15 studenti in una classe:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Possiamo utilizzare la funzione lm() per utilizzare il metodo dei minimi quadrati per adattare una linea di regressione a questi dati:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Dai valori nella colonna Risultato stimato , possiamo scrivere la seguente linea di regressione adattata:

Punteggio esame = 65.334 + 1.982 (ore)

Ecco come interpretare ciascun coefficiente nel modello:

• Intercetta : Per uno studente che studia 0 ore, il punteggio atteso dell’esame è 65.334 .
• ore : Per ogni ora aggiuntiva studiata, il punteggio previsto dell’esame aumenta di 1.982 .

Possiamo utilizzare questa equazione per stimare il voto dell’esame che uno studente riceverà in base alle ore di studio.

Ad esempio, se uno studente studia per 5 ore, stimeremmo che il punteggio dell’esame sarebbe 75.244:

Punteggio esame = 65.334 + 1.982(5) = 75.244

Infine, possiamo creare un grafico a dispersione dei dati originali con la linea di regressione adattata sovrapposta al grafico:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

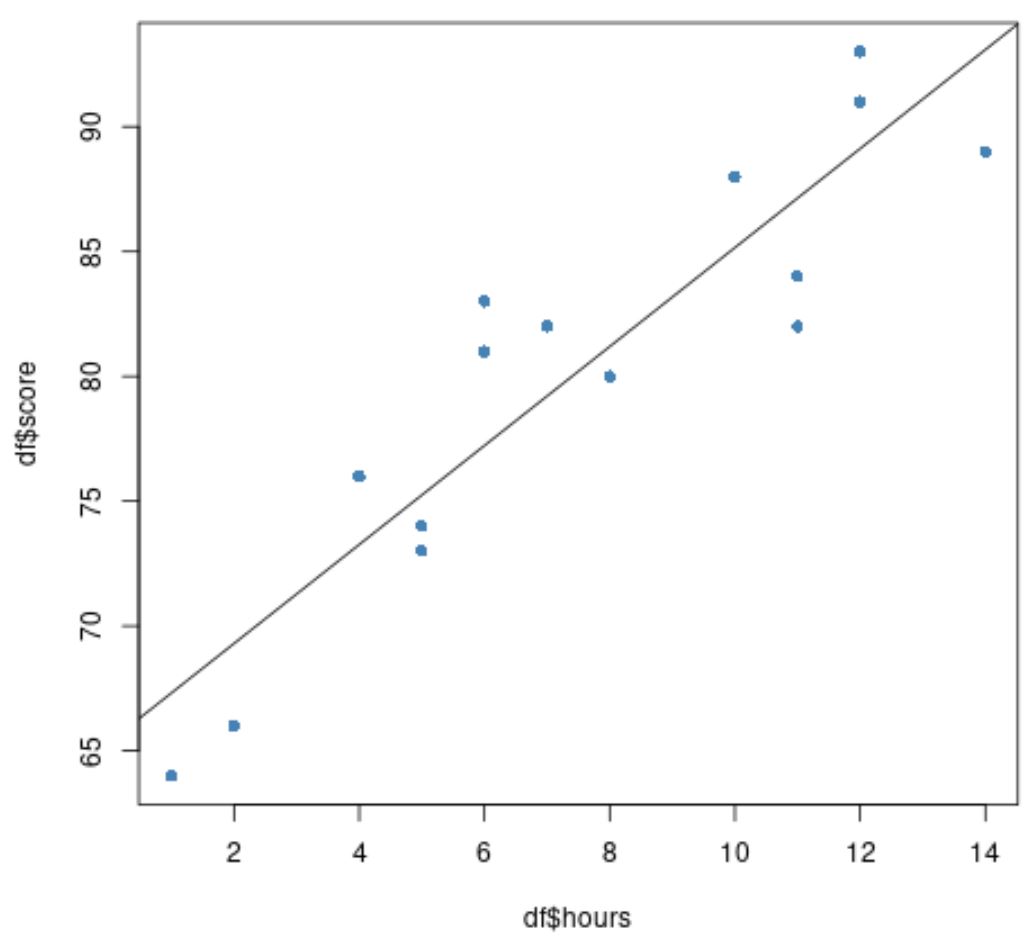
I cerchi blu rappresentano i dati e la linea nera rappresenta la linea di regressione adattata.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come creare una trama residua in R
Come testare la multicollinearità in R
Come eseguire l’adattamento della curva in R