Come utilizzare il metodo elbow in r per trovare cluster ottimali

Uno degli algoritmi di clustering più comunemente utilizzati nell’apprendimento automatico è noto come clustering k-means .

Il clustering K-means è una tecnica in cui inseriamo ciascuna osservazione da un set di dati in uno dei cluster K.

L’obiettivo finale è quello di avere K cluster in cui le osservazioni all’interno di ciascun cluster sono abbastanza simili tra loro mentre le osservazioni nei diversi cluster sono abbastanza diverse l’una dall’altra.

Quando si esegue il clustering k-means, il primo passo è scegliere un valore per K , ovvero il numero di cluster in cui vogliamo inserire le osservazioni.

Uno dei modi più comuni per scegliere un valore per K è noto come metodo del gomito , che prevede la creazione di un grafico con il numero di cluster sull’asse x e il totale della somma dei quadrati sull’asse y, quindi identificare dove nella trama appare un “ginocchio” o una svolta.

Il punto sull’asse x in cui si trova il “ginocchio” ci dice il numero ottimale di cluster da utilizzare nell’algoritmo di clustering k-means.

L’esempio seguente mostra come utilizzare il metodo del gomito in R.

Esempio: utilizzo del metodo del gomito in R

Per questo esempio, utilizzeremo il set di dati USArrests integrato in R, che contiene il numero di arresti ogni 100.000 persone in ciascuno stato degli Stati Uniti nel 1973 per omicidio, aggressione e stupro, nonché la percentuale della popolazione di ciascuno stato che vive in aree urbane. le zone. , UrbanPop.

Il codice seguente mostra come caricare il set di dati, rimuovere le righe con valori mancanti e ridimensionare ciascuna variabile nel set di dati per avere una media pari a 0 e una deviazione standard pari a 1:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Per trovare il numero ottimale di cluster da utilizzare nell’algoritmo k-means, utilizzeremo la funzione fviz_nbclust() dal pacchetto factoextra per creare un grafico del numero di cluster rispetto al totale nella somma dei quadrati:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

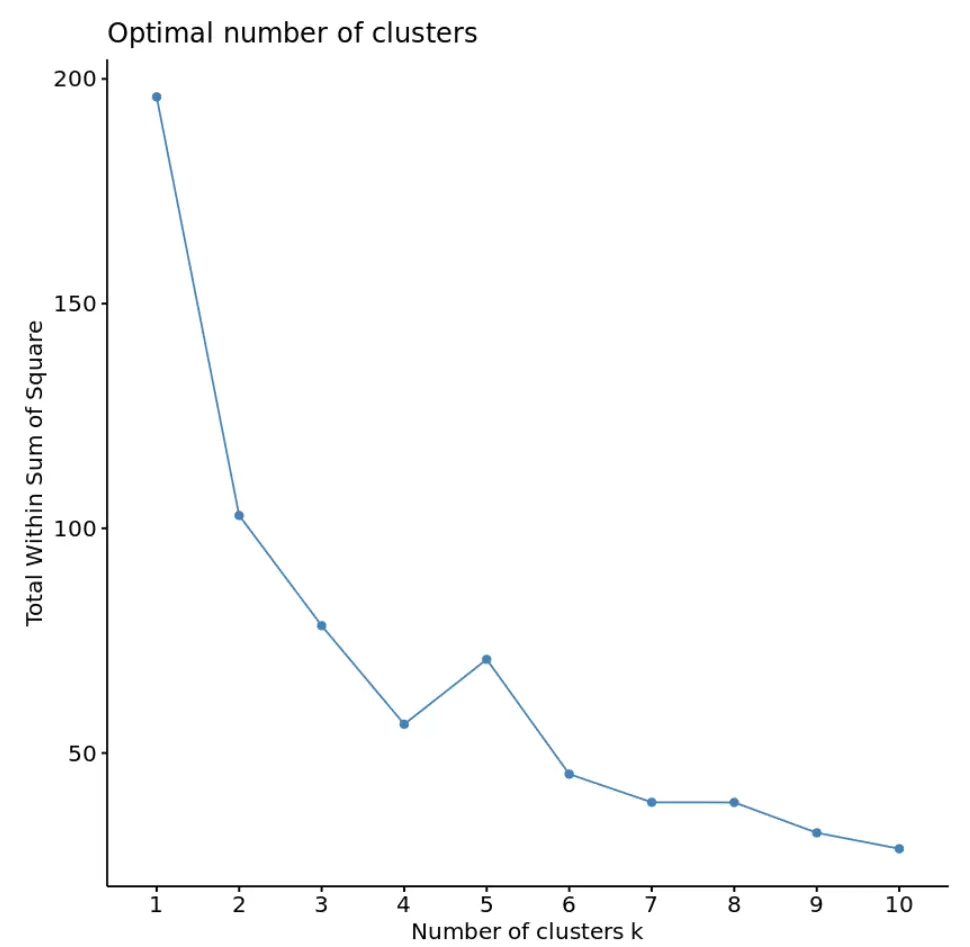
In questo grafico sembra che ci sia un “ginocchio” o una piega in corrispondenza di k = 4 cluster. Questo è il punto in cui il totale nella somma dei quadrati inizia a stabilizzarsi.

Questo ci dice che il numero ottimale di cluster da utilizzare nell’algoritmo k-means è 4.

Nota : anche se potremmo ottenere un totale inferiore nella somma dei quadrati utilizzando più cluster, probabilmente adatteremmo eccessivamente i dati di addestramento e pertanto l’algoritmo k-medie non funzionerebbe altrettanto bene sui dati di test.

Possiamo utilizzare la funzione kmeans() dal pacchetto cluster per eseguire il clustering k-means sul set di dati utilizzando il valore ottimale per k di 4:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Dai risultati possiamo vedere che:

• 16 stati sono stati assegnati al primo cluster
• 13 stati sono stati assegnati al secondo cluster
• 13 stati sono stati assegnati al terzo cluster
• 8 stati sono stati assegnati al quarto cluster

Possiamo anche aggiungere le assegnazioni dei cluster di ciascuno stato al set di dati originale:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Ciascuna osservazione del database originale è stata inserita in uno dei quattro gruppi.

Risorse addizionali

I seguenti tutorial forniscono esempi dettagliati su come eseguire vari algoritmi di clustering in R:

Clustering delle medie K in R: esempio passo passo
Clustering K-Medoidi in R: esempio passo passo
Clustering gerarchico in R: esempio passo passo