Minimi quadrati parziali in r (passo dopo passo)

Uno dei problemi più comuni che incontrerai nell’apprendimento automatico è la multicollinearità . Ciò si verifica quando due o più variabili predittive in un set di dati sono altamente correlate.

Quando ciò accade, un modello potrebbe essere in grado di adattarsi bene a un set di dati di addestramento, ma potrebbe funzionare male su un nuovo set di dati che non ha mai visto perché si adatta eccessivamente al set di dati di addestramento. insieme di formazione.

Un modo per aggirare questo problema è utilizzare un metodo chiamato minimi quadrati parziali , che funziona come segue:

• Standardizzare le variabili predittive e di risposta.
• Calcolare M combinazioni lineari (chiamate “componenti PLS”) delle p variabili predittive originali che spiegano una quantità significativa di variazione sia nella variabile di risposta che nelle variabili predittive.
• Utilizzare il metodo dei minimi quadrati per adattare un modello di regressione lineare utilizzando i componenti PLS come predittori.
• Utilizza la convalida incrociata k-fold per trovare il numero ottimale di componenti PLS da mantenere nel modello.

Questo tutorial fornisce un esempio passo passo di come eseguire i minimi quadrati parziali in R.

Passaggio 1: caricare i pacchetti necessari

Il modo più semplice per eseguire i minimi quadrati parziali in R è utilizzare le funzioni nel pacchetto pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Passaggio 2: adattare il modello dei minimi quadrati parziali

Per questo esempio, utilizzeremo il set di dati R integrato chiamato mtcars che contiene dati su diversi tipi di auto:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Per questo esempio, adatteremo un modello dei minimi quadrati parziali (PLS) utilizzando hp come variabile di risposta e le seguenti variabili come variabili predittive:

• mpg
• Schermo
• merda
• peso
• qsec

Il codice seguente mostra come adattare il modello PLS a questi dati. Nota i seguenti argomenti:

• scale=TRUE : indica a R che ciascuna delle variabili nel set di dati deve essere ridimensionata per avere una media pari a 0 e una deviazione standard pari a 1. Ciò garantisce che nessuna variabile predittrice abbia troppa influenza nel modello se misurata in unità diverse.
• validation=”CV” : indica a R di utilizzare la convalida incrociata k-fold per valutare le prestazioni del modello. Tieni presente che per impostazione predefinita vengono utilizzate k=10 pieghe. Tieni inoltre presente che puoi specificare “LOOCV” invece di eseguire la convalida incrociata Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Passaggio 3: scegli il numero di componenti PLS

Una volta montato il modello, dobbiamo determinare quanti componenti PLS conservare.

Per fare ciò, basta guardare l’errore quadratico medio della radice del test (test RMSE) calcolato mediante convalida k-cross:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

Nel risultato ci sono due tabelle interessanti:

1. CONVALIDA: RMSEP

Questa tabella ci dice il test RMSE calcolato mediante convalida incrociata k-fold. Possiamo vedere quanto segue:

• Se utilizziamo solo il termine originale nel modello, l’RMSE del test è 69,66 .
• Se aggiungiamo il primo componente PLS, il test RMSE scende a 40,57.
• Se aggiungiamo il secondo componente PLS, il test RMSE scende a 35,48.

Possiamo vedere che l’aggiunta di ulteriori componenti PLS si traduce effettivamente in un aumento dell’RMSE del test. Sembra quindi che sarebbe ottimale utilizzare solo due componenti PLS nel modello finale.

2. FORMAZIONE: % di varianza spiegata

Questa tabella ci indica la percentuale di varianza nella variabile di risposta spiegata dai componenti PLS. Possiamo vedere quanto segue:

• Utilizzando solo la prima componente PLS, possiamo spiegare il 68,66% della variazione nella variabile di risposta.
• Aggiungendo la seconda componente PLS possiamo spiegare l’ 89,27% della variazione della variabile risposta.

Si noti che saremo comunque in grado di spiegare una maggiore varianza utilizzando più componenti PLS, ma possiamo vedere che l’aggiunta di più di due componenti PLS in realtà non aumenta di molto la percentuale di varianza spiegata.

Possiamo anche visualizzare il test RMSE (insieme al test MSE e R-squared) in funzione del numero di componenti PLS utilizzando la funzione validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

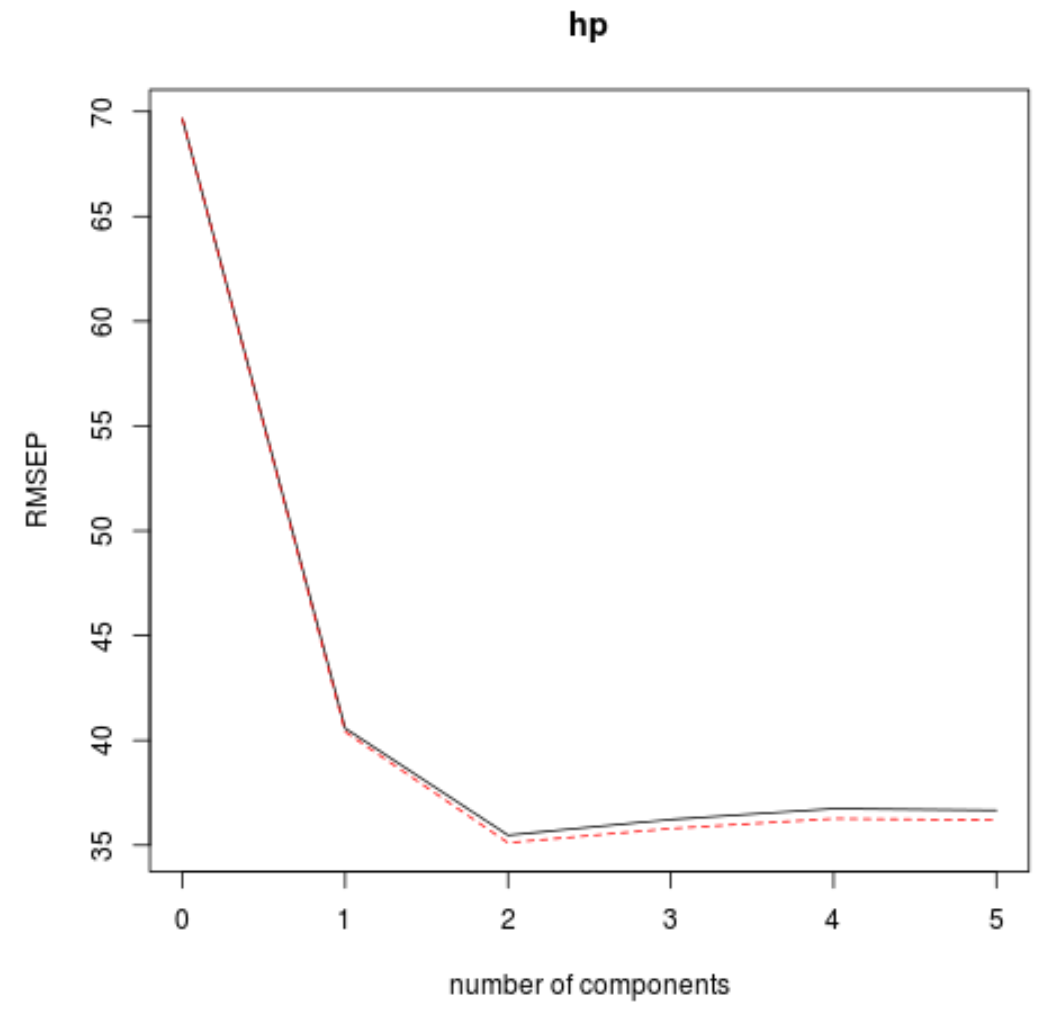
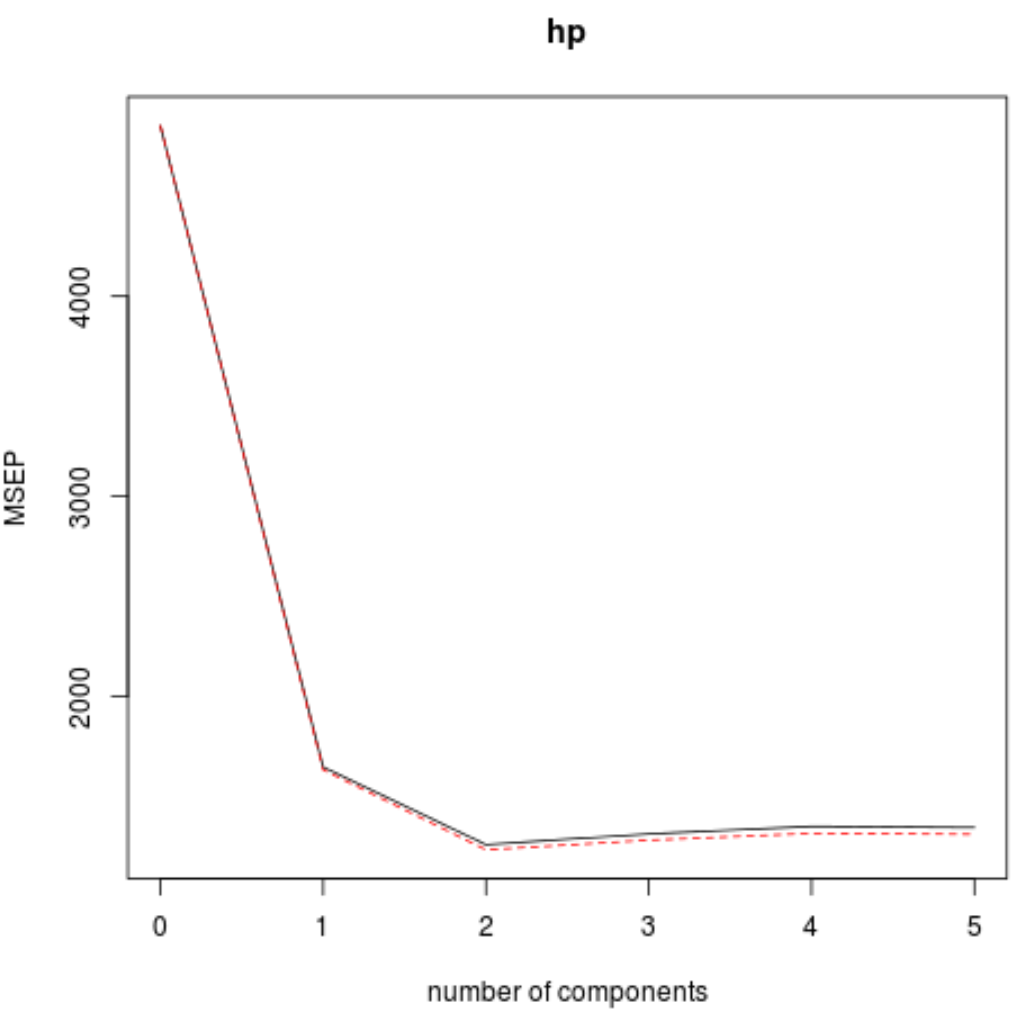
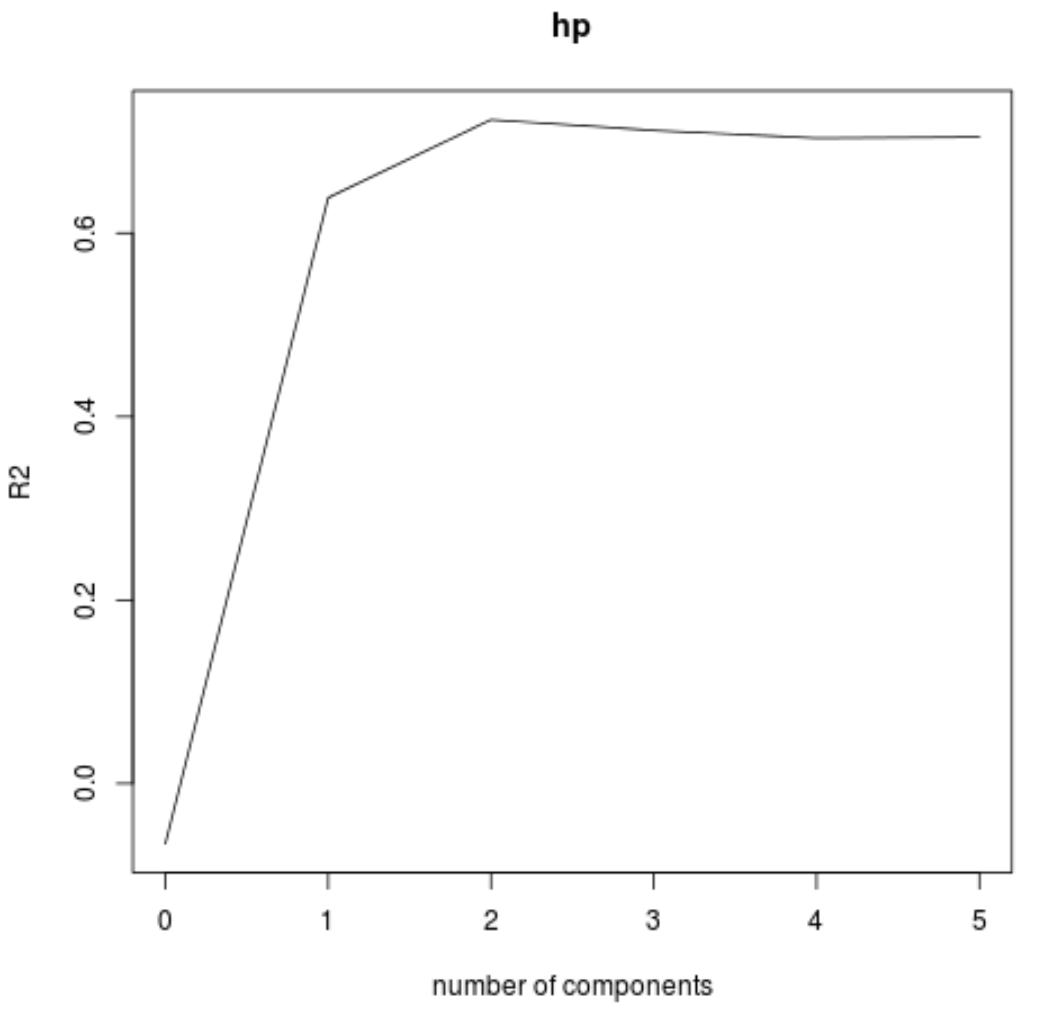
In ogni grafico, possiamo vedere che l’adattamento del modello migliora aggiungendo due componenti PLS, ma tende a peggiorare quando aggiungiamo più componenti PLS.

Pertanto, il modello ottimale include solo i primi due componenti PLS.

Passaggio 4: utilizzare il modello finale per fare previsioni

Possiamo utilizzare il modello finale con due componenti PLS per fare previsioni su nuove osservazioni.

Il codice seguente mostra come suddividere il set di dati originale in un set di training e un set di test e utilizzare il modello finale con due componenti PLS per effettuare previsioni sul set di test.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Vediamo che l’RMSE del test risulta essere 54.89609 . Questa è la deviazione media tra il valore hp previsto e il valore hp osservato per le osservazioni del set di test.

Si noti che un modello di regressione delle componenti principali equivalenti con due componenti principali ha prodotto un RMSE di test di 56.86549 . Pertanto, il modello PLS ha leggermente sovraperformato il modello PCR per questo set di dati.

L’utilizzo completo del codice R in questo esempio può essere trovato qui .