Come eseguire la regressione dei minimi quadrati ponderati in r

Uno dei presupposti chiave della regressione lineare è che i residui siano distribuiti con uguale varianza a ciascun livello della variabile predittrice. Questa ipotesi è nota come omoschedasticità .

Quando questa assunzione non è rispettata, si dice che nei residui è presente eteroschedasticità . Quando ciò accade, i risultati della regressione diventano inaffidabili.

Un modo per risolvere questo problema è utilizzare la regressione dei minimi quadrati ponderati , che assegna pesi alle osservazioni in modo tale che quelle con una varianza di errore bassa ricevano più peso perché contengono più informazioni rispetto alle osservazioni con una varianza di errore maggiore.

Questo tutorial fornisce un esempio passo passo di come eseguire la regressione dei minimi quadrati ponderati in R.

Passaggio 1: creare i dati

Il codice seguente crea un data frame contenente il numero di ore studiate e il corrispondente punteggio dell’esame per 16 studenti:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Passaggio 2: eseguire la regressione lineare

Successivamente, utilizzeremo la funzione lm() per adattare un semplice modello di regressione lineare che utilizza le ore come variabile predittiva e il punteggio come variabile di risposta :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Passaggio 3: test dell’eteroschedasticità

Successivamente, creeremo un grafico dei residui e dei valori adattati per verificare visivamente l’eteroschedasticità:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

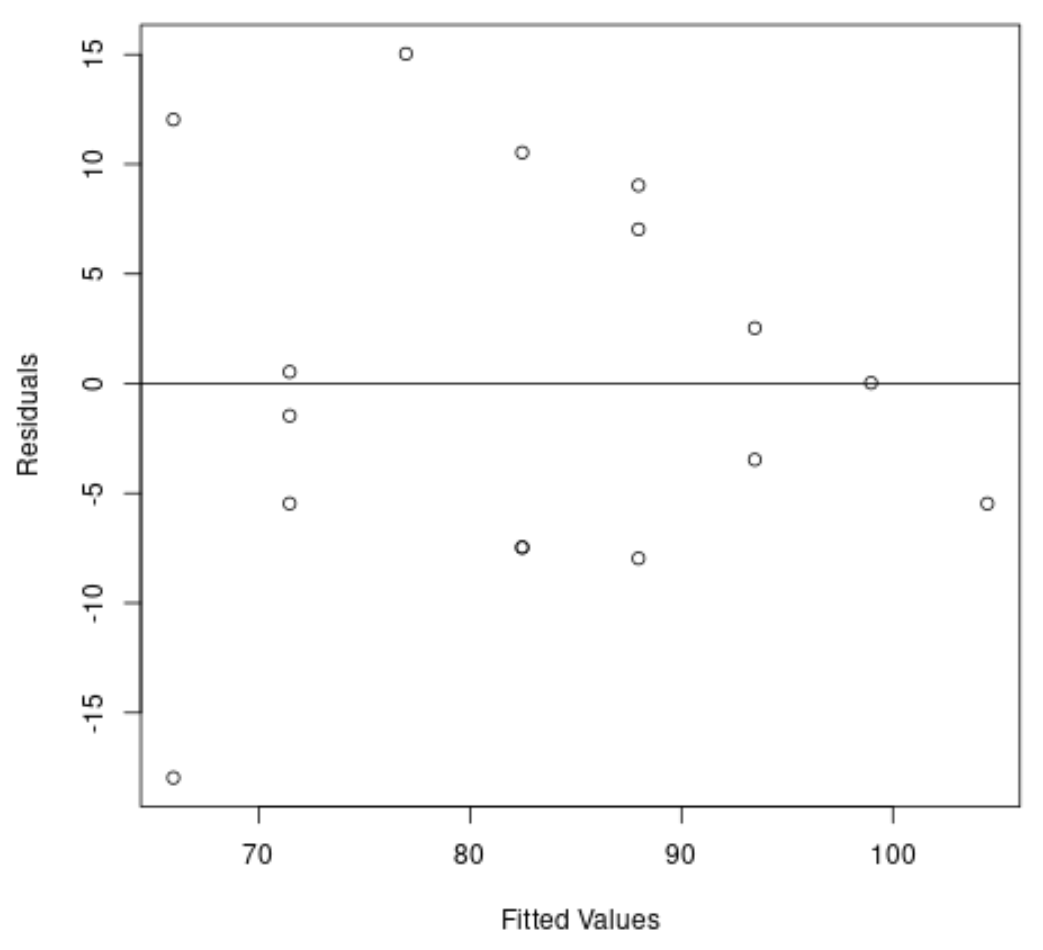
Possiamo vedere dal grafico che i residui hanno una forma “a cono”: non sono distribuiti con uguale varianza in tutto il grafico.

Per testare formalmente l’eteroschedasticità, possiamo eseguire un test di Breusch-Pagan:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Il test di Breusch-Pagan utilizza le seguenti ipotesi nulle e alternative :

• Ipotesi nulla (H ₀ ): è presente omoschedasticità (i residui sono distribuiti con uguale varianza)
• Ipotesi alternativa ( _HA ): è presente eteroschedasticità (i residui non sono distribuiti con uguale varianza)

Poiché il valore p del test è 0,0466 , rifiuteremo l’ipotesi nulla e concluderemo che l’eteroschedasticità è un problema in questo modello.

Passaggio 4: eseguire la regressione dei minimi quadrati ponderati

Poiché è presente l’eteroschedasticità, eseguiremo i minimi quadrati ponderati impostando i pesi in modo tale che le osservazioni con varianza inferiore ricevano più peso:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

Dai risultati, possiamo vedere che la stima del coefficiente per la variabile predittrice delle ore è leggermente cambiata e l’adattamento complessivo del modello è migliorato.

Il modello dei minimi quadrati ponderati ha un errore standard residuo di 1,199 , rispetto a 9,224 nel modello di regressione lineare semplice originale.

Ciò indica che i valori previsti prodotti dal modello dei minimi quadrati ponderati sono molto più vicini alle osservazioni effettive rispetto ai valori previsti prodotti dal modello di regressione lineare semplice.

Il modello dei minimi quadrati ponderati ha anche un R quadrato di 0,6762 , rispetto a 0,6296 nel modello di regressione lineare semplice originale.

Ciò indica che il modello dei minimi quadrati ponderati è in grado di spiegare maggiormente la varianza nei punteggi degli esami rispetto al semplice modello di regressione lineare.

Queste misurazioni indicano che il modello dei minimi quadrati ponderati fornisce un migliore adattamento ai dati rispetto al modello di regressione lineare semplice.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione quantile in R