Misura di prova

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la dimensione del campione e perché è importante nelle statistiche. Inoltre, scoprirai come calcolare la dimensione appropriata del campione e un esercizio risolto in modo da poter vedere come viene eseguito.

Qual è la dimensione del campione?

La dimensione del campione (o dimensione del campione ) è il numero di individui che compongono il campione di uno studio. Nelle statistiche, la dimensione del campione è importante affinché il campione sia rappresentativo dell’intera popolazione.

Pertanto, la dimensione del campione di uno studio statistico deve essere sufficientemente ampia da rappresentare le caratteristiche dell’intera popolazione. D’altro canto la dimensione del campione non può essere eccessivamente ampia perché la ricerca diventerebbe più costosa. In conclusione, la dimensione del campione dovrebbe essere adeguata, né troppo grande né troppo piccola.

Se ad esempio vogliamo fare un’analisi sull’altezza di un paese, non possiamo chiedere l’altezza di tutti gli abitanti del paese, perché il rilievo richiederebbe molto tempo e sarebbe troppo costoso. È quindi necessario effettuare un campionamento casuale e intervistare solo un campione rappresentativo della popolazione.

➤ Vedi: Tipologie di campionamento

E come possiamo conoscere la dimensione appropriata del campione? Nella sezione successiva vedremo come determinare la dimensione del campione adeguata in base ai requisiti della ricerca.

Come calcolare la dimensione del campione

Per stimare una media, la dimensione del campione richiesta è uguale al quadrato di Z _α/2 moltiplicato per la deviazione standard (σ) diviso per il margine di errore desiderato (e). La formula per calcolare la dimensione del campione è quindi:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Oro:

$n$

è la dimensione del campione.
$\alpha$

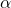
è il livello di significatività desiderato. Tenendo conto di questo

$1-\alpha$

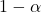
è il livello di confidenza desiderato.
$Z_{\alpha/2}$

è il quantile della distribuzione normale standard corrispondente a una probabilità di α/2. Per campioni di grandi dimensioni e un livello di confidenza del 95% è solitamente vicino a 1,96 mentre per un livello di confidenza del 99% è solitamente vicino a 2,576.
$\sigma$

è la deviazione standard.

Tieni presente che in questa formula si presuppone che la dimensione della popolazione sia infinita, ovvero che la dimensione della popolazione sia molto grande o sconosciuta.

Nota: la formula precedente deriva dall’intervallo della formula di confidenza per la media .

Esempio di calcolo della dimensione del campione

In questa sezione, calcoleremo come esempio la dimensione del campione appropriata per un’indagine statistica.

Sappiamo che la deviazione standard di una popolazione è intorno a 15, ma non ne conosciamo la media, quindi vogliamo effettuare uno studio per stimare la media. Di quale dimensione del campione abbiamo bisogno se vogliamo un margine di errore di ±2 con un livello di confidenza del 95%?

Come abbiamo visto sopra, la formula per calcolare la dimensione del campione è:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

In questo caso, il livello di confidenza desiderato è del 95%, quindi il valore Z _α/2 corrispondente è 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Vedi: Tabella con i valori del livello di confidenza

Infine, ora che sappiamo quanto valgono tutti i parametri, sostituiamo i loro valori nella formula e calcoliamo la dimensione del campione:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

In breve, per stimare la media della popolazione con i requisiti desiderati, abbiamo bisogno di almeno un campione di 217 individui.

Dimensione del campione, livello di confidenza e margine di errore

A seconda del livello di confidenza e del margine di errore richiesto, la dimensione del campione richiesta varierà. Pertanto, la dimensione del campione, il livello di confidenza e il margine di errore sono correlati come segue:

La dimensione del campione e il livello di confidenza sono direttamente proporzionali. Cioè, se il livello di confidenza aumenta, aumenterà anche la dimensione del campione.
La dimensione del campione e il margine di errore sono inversamente proporzionali. Pertanto, se il margine di errore aumenta, la dimensione del campione diminuirà.
Pertanto, aumentare la dimensione del campione può aumentare il livello di confidenza o ridurre il margine di errore.

Altre formule per la dimensione del campione

A seconda del parametro da stimare, la formula per la dimensione del campione necessaria varia leggermente. Pertanto in questa sezione vedremo altre formule che possono essere utili per calcolare la numerosità del campione in alcuni casi particolari.

dimensione del campione di una proporzione

La formula per calcolare la dimensione del campione necessaria per stimare una proporzione (p) è:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

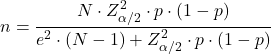
Dimensione campionaria di una probabilità

Quando si desidera stimare una probabilità, si consiglia di utilizzare la seguente formula per determinare la dimensione del campione necessaria:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Dimensione del campione per il confronto di due medie indipendenti

La formula per calcolare la dimensione del campione quando si confrontano due medie indipendenti con un dato rischio α e rischio β è la seguente:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Oro

$\Delta$

è la differenza tra le due medie dell’ipotesi alternativa.

Dimensione del campione per il confronto di due medie appaiate

Se si vogliono confrontare due medie accoppiate con errore α ed errore β fissi, la formula da utilizzare per trovare il numero di osservazioni nel campione è:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Oro

$\Delta$

è la differenza tra le due medie accoppiate dell’ipotesi alternativa e

$\sigma_d^2$

È la varianza delle differenze tra due misurazioni dello stesso individuo.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più