Misure di tendenza centrale: definizione ed esempi
Una misura della tendenza centrale è un singolo valore che rappresenta il punto centrale di un set di dati. Questo valore può anche essere chiamato la “posizione centrale” di un set di dati.
In statistica, ci sono tre misure comuni di tendenza centrale:
- La media
- La mediana
- La moda
Ognuna di queste misure trova la posizione centrale di un set di dati utilizzando metodi diversi. A seconda del tipo di dati che stai analizzando, potrebbe essere meglio utilizzare uno di questi tre parametri piuttosto che gli altri due.
In questo articolo vedremo come calcolare ciascuna delle tre misure di tendenza centrale e come determinare quale misura è meglio utilizzare in base ai dati.
Perché sono utili le misure di tendenza centrale?
Prima di esaminare come calcolare la media, la mediana e la moda, è utile capire innanzitutto perché queste misurazioni sono effettivamente utili.
Considera il seguente scenario:
Una giovane coppia sta cercando di decidere dove acquistare la prima casa in una nuova città e il massimo che può spendere è $ 150.000. Alcune zone della città hanno case costose, altre hanno case economiche e altre hanno case a prezzo medio. Vogliono restringere facilmente la ricerca a quartieri specifici che si adattano al loro budget.
Se la coppia si limitasse a guardare i prezzi delle case unifamiliari in ciascun quartiere, potrebbe avere difficoltà a determinare quali quartieri si adattano meglio al loro budget, perché potrebbero vedere qualcosa di simile a questo:
Prezzi delle case del quartiere A : $ 140.000, $ 190.000, $ 265.000, $ 115.000, $ 270.000, $ 240.000, $ 250.000, $ 180.000, $ 160.000, $ 200.000, $ 240.000, $ 280.000, …
Prezzi delle case nel quartiere B : $ 140.000, $ 290.000, $ 155.000, $ 165.000, $ 280.000, $ 220.000, $ 155.000, $ 185.000, $ 160.000, $ 200.000, $ 190.000, $ 140.000, $ 145.0 00,…
Prezzi delle case nel quartiere C : $ 140.000, $ 130.000, $ 165.000, $ 115.000, $ 170.000, $ 100.000, $ 150.000, $ 180.000, $ 190.000, $ 120.000, $ 110.000, $ 130.000, $ 120,0 00,…
Tuttavia, se conoscessero il prezzo medio (ad esempio una misura della tendenza centrale) delle case in ciascun quartiere, allora potrebbero affinare la ricerca molto più rapidamente perché potrebbero identificare più facilmente quale quartiere ha prezzi delle case che corrispondono al loro budget:
Prezzo medio di una casa nel quartiere A: $ 220.000
Prezzo medio di una casa nel quartiere B : $ 190.000
Prezzo medio di una casa nel quartiere C : $ 140.000
Conoscendo il prezzo medio delle case in ciascun quartiere, possono vedere rapidamente che è probabile che il quartiere C abbia il maggior numero di case disponibili entro il loro budget.
Questo è il vantaggio di utilizzare una misura di tendenza centrale: aiuta a comprendere il valore centrale di un set di dati, che tende a descrivere dove si trovano generalmente i valori dei dati. In questo particolare esempio, aiuta la giovane coppia a capire il prezzo tipico di una casa in ogni quartiere.
Conclusione: una misura della tendenza centrale è utile perché ci fornisce un singolo valore che descrive il “centro” di un set di dati. Questo ci aiuta a comprendere un set di dati molto più velocemente rispetto alla semplice osservazione di tutti i singoli valori nel set di dati.
Significare
La misura della tendenza centrale più comunemente utilizzata è la media . Per calcolare la media di un set di dati, è sufficiente sommare tutti i singoli valori e dividerli per il numero totale di valori.
Media = (somma di tutti i valori) / (numero totale di valori)
Ad esempio, supponiamo di avere il seguente set di dati che mostra il numero di fuoricampo realizzati da 10 giocatori di baseball della stessa squadra durante una stagione:
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Il numero medio di fuoricampo realizzati per giocatore può essere calcolato come segue:
Media = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 circuiti .
Mediano
La mediana è il valore medio di un set di dati. Puoi trovare la mediana ordinando tutti i singoli valori in un set di dati dal più piccolo al più grande e trovando il valore mediano. Se è presente un numero dispari di valori, la mediana è il valore medio. Se il numero di valori è pari, la mediana è la media dei due valori medi.
Ad esempio, per trovare il numero medio di fuoricampo realizzati dai 10 giocatori di baseball nell’esempio precedente, possiamo classificare i giocatori in ordine decrescente in base al numero di fuoricampo realizzati:
| Giocatore | #1 | #6 | #7 | #5 | #dieci | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Poiché abbiamo un numero pari di valori, la mediana è semplicemente la media dei due valori medi: 13,5 .
Consideriamo invece se avessimo nove giocatori:
| Giocatore | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
In questo caso, poiché abbiamo un numero dispari di valori, la mediana è semplicemente il valore medio: 14 .
La moda
La moda è il valore che appare più spesso in un set di dati. Un set di dati non può avere modalità (se non ci sono valori ripetuti), una modalità o più modalità.
Ad esempio, il seguente set di dati non ha modalità:
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Il seguente set di dati ha una modalità: 15 . Questo è il valore che appare più frequentemente.
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Il seguente set di dati ha tre modalità: 8, 15, 19 . Questi sono i valori che compaiono più frequentemente.
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
La moda può essere una misura particolarmente utile della tendenza centrale quando si lavora con dati categorici, perché ci dice quale categoria appare più frequentemente. Ad esempio, considera il seguente grafico a barre che mostra i risultati di un sondaggio sul colore preferito delle persone:
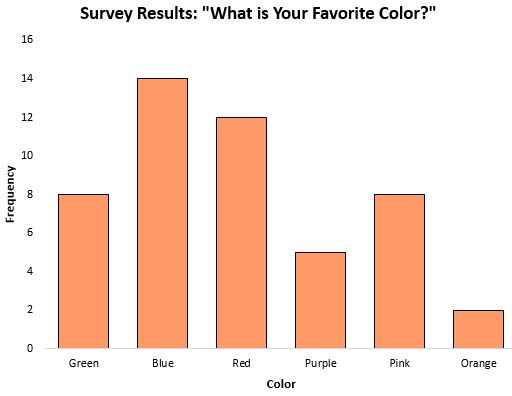
La modalità , ovvero la risposta che si è verificata più frequentemente, è stata quella blu.
Negli scenari in cui i dati sono categorici (come quello sopra), non è nemmeno possibile calcolare la mediana o la media, quindi la moda è l’unica misura della tendenza centrale che possiamo utilizzare.
La modalità può essere utilizzata anche per dati numerici, come abbiamo visto nell’esempio precedente con i giocatori di baseball. Tuttavia, la modalità tende ad essere meno utile per rispondere alla domanda “Qual è un valore tipico per questo set di dati?” »
Ad esempio, supponiamo di voler conoscere il numero tipico di fuoricampo realizzati da un giocatore di baseball di questa squadra:
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
La modalità per questo set di dati è 8, 15 e 19 perché questi sono i valori più frequenti. Tuttavia, questi dati non sono molto utili per comprendere il numero tipico di fuoricampo realizzati da un giocatore della squadra. Una misura migliore della tendenza centrale in questo caso sarebbe la mediana (15) o la media (anche 15).
La moda è anche una misura inadeguata della tendenza centrale quando è un numero lontano dal resto dei valori. Ad esempio, la modalità del set di dati seguente è 30, ma in realtà non rappresenta il numero “tipico” di fuoricampo per giocatore della squadra:
| Giocatore | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #dieci |
|---|---|---|---|---|---|---|---|---|---|---|
| Fuoricampo | 5 | 6 | 7 | dieci | 11 | 12 | 13 | 15 | 30 | 30 |
Ancora una volta, la media o la mediana farebbero un lavoro migliore nel descrivere la posizione centrale di questo set di dati.
Quando utilizzare Media, Mediana e Moda
Abbiamo visto che la media, la mediana e la moda misurano tutte la posizione centrale, o “valore tipico”, di un set di dati in modi molto diversi:
Media: trova il valore medio in un set di dati.
Mediana: trova il valore mediano in un set di dati.
Modalità: trova il valore più frequente in un set di dati.
Ecco gli scenari in cui alcune misure di tendenza centrale sono migliori da utilizzare rispetto ad altre:
Quando utilizzare la media
È preferibile utilizzare la media quando la distribuzione dei dati è abbastanza simmetrica e non sono presenti valori anomali.
Ad esempio, supponiamo di avere la seguente distribuzione che mostra gli stipendi degli individui in una determinata città:

Poiché questa distribuzione è abbastanza simmetrica (vale a dire se la dividessi a metà, ciascuna metà sembrerebbe più o meno uguale) e non ci sono valori anomali (vale a dire (diciamo senza stipendi estremamente alti), la media farà un buon lavoro nel descrivere questo set di dati.
La media risulta essere $ 63.000, che è più o meno al centro della distribuzione:

Quando utilizzare la mediana
È preferibile utilizzare la mediana quando la distribuzione dei dati è distorta o quando sono presenti valori anomali.
Dati distorti:
Quando la distribuzione è distorta, la mediana riesce comunque a catturare la posizione centrale. Ad esempio, consideriamo la seguente distribuzione degli stipendi degli individui in una determinata città:

La mediana riflette meglio la retribuzione “tipica” di un individuo rispetto alla media. Questo perché valori elevati alla coda di una distribuzione tendono a spostare la media lontano dal centro e verso la coda lunga.
In questo esempio particolare, la media ci dice che un individuo tipico guadagna circa 47.000 dollari all’anno in questa città, mentre la mediana ci dice che un individuo tipico guadagna solo circa 32.000 dollari all’anno, il che è molto più rappresentativo dell’individuo tipico.
Valori anomali:
La mediana aiuta inoltre a catturare meglio la posizione centrale di una distribuzione quando nei dati sono presenti valori anomali. Ad esempio, considera il seguente grafico che mostra la metratura delle case in una determinata strada:

La media è fortemente influenzata da alcune case estremamente grandi, mentre la mediana non lo è. Pertanto, la mediana fa un lavoro migliore nel catturare la metratura “tipica” di una casa su quella strada rispetto alla media.
Quando utilizzare la modalità
Questa modalità è particolarmente utile quando si lavora con dati categorici e si desidera sapere quale categoria appare più frequentemente. Ecco alcuni esempi:
- Stai conducendo un sondaggio sui colori preferiti dalle persone e desideri sapere quale colore appare più frequentemente nelle risposte.
- Stai conducendo un sondaggio sulle preferenze delle persone tra tre scelte per il design del sito web e vuoi sapere quale design le persone preferiscono di più.
Come accennato in precedenza, se si lavora con dati categoriali, non è nemmeno possibile calcolare la mediana, il che lascia la moda come unica misura della tendenza centrale.
In generale, se si lavora con dati numerici come la metratura delle case, il numero di fuoricampo effettuati per giocatore, lo stipendio per individuo, ecc., di solito è meglio utilizzare la mediana o la media per descrivere il valore “tipico” in il set di dati.
Nota: è importante notare che se un set di dati è distribuito perfettamente normalmente, allora la media, la mediana e la moda hanno tutte lo stesso valore.