Le tre ipotesi di misure ripetute anova

Un’ANOVA a misure ripetute viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi in cui compaiono gli stessi soggetti in ciascun gruppo.

Tuttavia, prima di eseguire un’ANOVA a misure ripetute, dobbiamo garantire che siano soddisfatte le seguenti ipotesi:

1. Indipendenza: ogni osservazione deve essere indipendente.

2. Normalità: la distribuzione della variabile di risposta è distribuita normalmente.

3. Sfericità: le varianze delle differenze tra tutte le combinazioni di gruppi correlati devono essere uguali.

Se una o più di queste ipotesi vengono violate, i risultati delle misure ripetute ANOVA potrebbero essere inaffidabili.

In questo articolo forniamo una spiegazione per ciascun presupposto, come determinare se il presupposto è soddisfatto e cosa fare se non viene soddisfatto.

Ipotesi 1: Indipendenza

Una misura ANOVA ripetuta presuppone che ciascuna osservazione nel set di dati sia indipendente da tutte le altre osservazioni.

Come determinare se questo presupposto è soddisfatto

Il modo più semplice per verificare questa ipotesi è verificare che ciascun individuo nel set di dati sia stato campionato casualmente dalla popolazione utilizzando un metodo di campionamento casuale .

Se è stato utilizzato un metodo di campionamento casuale, ogni osservazione può essere considerata indipendente.

Cosa fare se questo presupposto non viene rispettato

Se questo presupposto non viene soddisfatto, allora il problema è serio perché i valori di ciascun individuo possono essere correlati tra loro in un modo o nell’altro.

Spesso l’unico rimedio in questo scenario è reclutare individui per un nuovo studio utilizzando un metodo di campionamento casuale.

Ipotesi 2: normalità

Una misura ANOVA ripetuta presuppone che la distribuzione della variabile di risposta sia distribuita normalmente .

Come determinare se questo presupposto è soddisfatto

Esistono due modi per verificare se questa ipotesi è vera:

1. Crea un istogramma o un grafico QQ

È possibile verificare visivamente se la distribuzione della variabile di risposta è approssimativamente distribuita normalmente creando un istogramma o un grafico QQ.

Se crei un istogramma , controlla semplicemente che la distribuzione della variabile di risposta segua approssimativamente una forma a “campana”. Se è così, spesso puoi presumere che il presupposto di normalità sia soddisfatto:

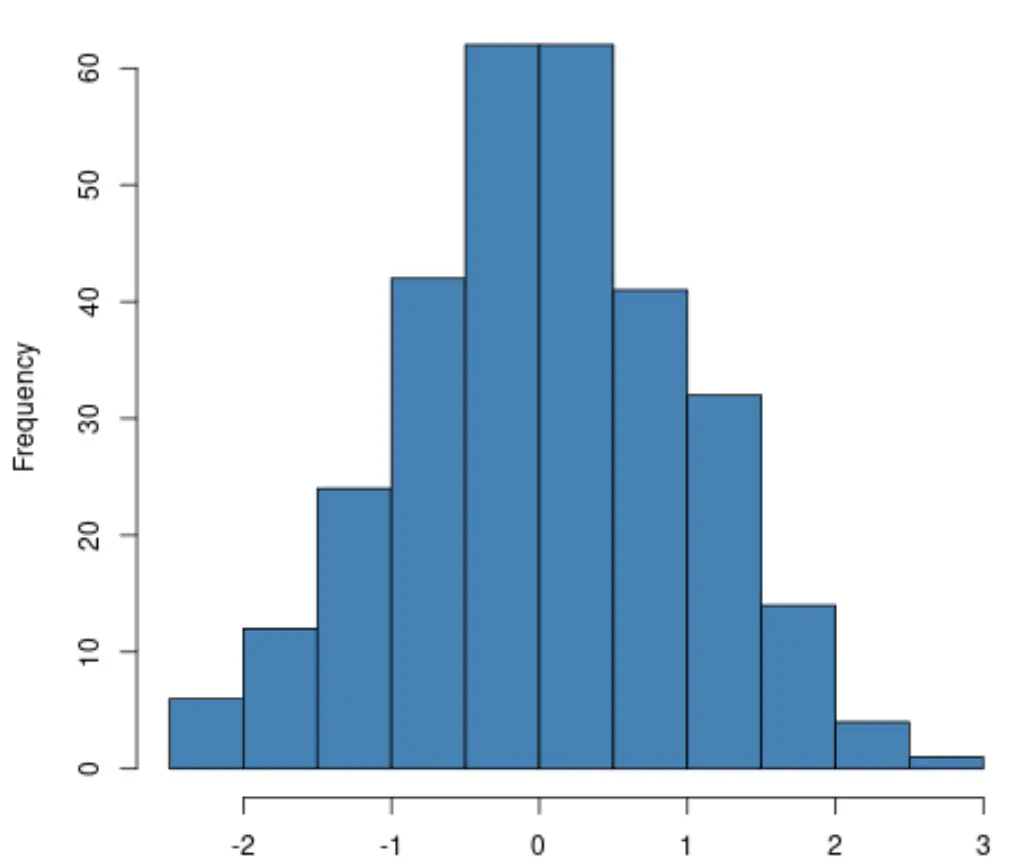
Se stai creando un grafico QQ , controlla se i punti dati si trovano lungo una linea diagonale retta. Se è così, in genere puoi presumere che il presupposto di normalità sia soddisfatto:

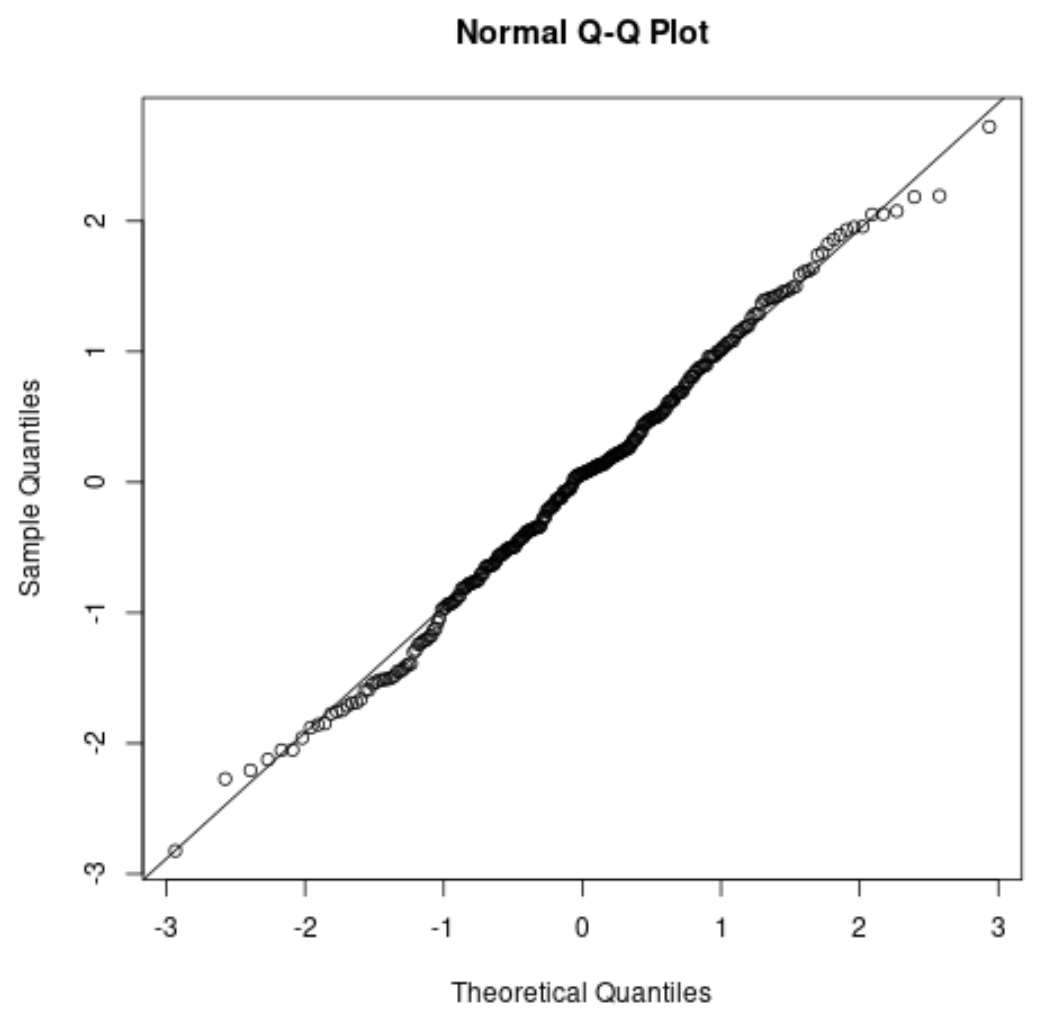
Correlato: Come utilizzare i grafici QQ per verificare la normalità

2. Eseguire un test statistico formale

Puoi anche eseguire un test di Shapiro-Wilk per verificare la normalità. Se il valore p del test è inferiore a 0,05, ciò suggerisce che i dati non sono distribuiti normalmente.

Tuttavia, tieni presente che quando lavori con campioni estremamente grandi, test statistici come il test di Shapiro-Wilk ti diranno quasi sempre che i tuoi dati non sono normali.

Per questo motivo, spesso è meglio ispezionare visivamente i dati utilizzando grafici come istogrammi e grafici QQ. Basta osservare i grafici per capire se i dati sono distribuiti normalmente oppure no.

Cosa fare se questo presupposto non viene rispettato

In generale, un’ANOVA a misure ripetute è considerata abbastanza robusta contro le violazioni del presupposto di normalità purché le dimensioni del campione siano sufficientemente grandi.

Se il presupposto della normalità viene gravemente violato, hai due scelte:

1. Trasforma i valori di risposta dei tuoi dati in modo che le distribuzioni siano distribuite più normalmente.

2. Eseguire un test non parametrico equivalente come il test di Friedman che non richiede l’assunzione di normalità.

Presupposto 3: Sfericità

Un’ANOVA a misure ripetute presuppone la sfericità , ovvero le varianze delle differenze tra tutte le combinazioni di gruppi correlati devono essere uguali.

Se questa ipotesi non viene soddisfatta, il rapporto F diventa gonfiato e i risultati delle misure ANOVA ripetute diventano inaffidabili.

Come determinare se questo presupposto è soddisfatto

Per verificare se questa ipotesi è soddisfatta, possiamo eseguire il test di sfericità di Mauchly.

Questo test utilizza la seguente ipotesi nulla e alternativa:

• H ₀ : Le varianze delle differenze sono uguali
• H _A : Le varianze delle differenze non sono uguali

Se il valore p del test è inferiore a un certo livello di significatività (ad esempio α = 0,05), allora rifiutiamo l’ipotesi nulla e concludiamo che le varianze delle differenze non sono uguali.

Altrimenti, se il valore p non è inferiore a un certo livello di significatività (ad esempio α = 0,05), non riusciamo a rifiutare l’ipotesi nulla e concludiamo che l’ipotesi di sfericità è soddisfatta.

A seconda del software statistico utilizzato, i risultati di questo test saranno simili a questi:

Poiché il valore p non è inferiore a 0,05, non riusciremo a rifiutare l’ipotesi nulla e concluderemo che l’ipotesi di sfericità è soddisfatta in questo particolare esempio.

Cosa fare se questo presupposto non viene rispettato

Se rifiutiamo l’ipotesi nulla del test di sfericità di Mauchly, generalmente applichiamo una correzione ai gradi di libertà utilizzati per calcolare il valore F nella tabella ANOVA a misure ripetute.

Ci sono tre correzioni che possiamo applicare:

• Huynh-Feldt (meno conservatore)
• Serre–Geisser
• Limite inferiore (più conservativo)

Ognuna di queste correzioni tende ad aumentare i valori p nella tabella di output dell’ANOVA a misure ripetute per tenere conto del fatto che il presupposto della sfericità è violato.

Possiamo quindi utilizzare questi valori p per determinare se dovremmo rifiutare o meno l’ipotesi nulla dell’ANOVA a misure ripetute.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulle misure ripetute ANOVA:

Un’introduzione all’ANOVA a misure ripetute
Calcolatore ANOVA per misure ripetute
Come riportare i risultati di un’ANOVA a misure ripetute
ANOVA a una via e ANOVA a misure ripetute: la differenza