Cos'è il sé di moran? (definizione & #038; esempio)

L’I di Moran è un modo per misurare l’autocorrelazione spaziale.

In poche parole, è un modo per quantificare quanto strettamente i valori sono raggruppati nello spazio 2D. Viene spesso utilizzato in geografia e scienza dell’informazione geografica (GIS) per misurare quanto strettamente le diverse caratteristiche sono raggruppate su una mappa, come il reddito familiare, il livello di istruzione, ecc.

L’Io di Moran: la formula

La formula per calcolare l’I di Moran è:

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

Oro:

• N: il numero di unità spaziali indicizzate da i e j
• W: La somma di tutti i w _ij
• x: La variabile di interesse (reddito familiare, anni di scolarizzazione, ecc.)
• x : la media di x
• w _ij : Una matrice di pesi spaziali

Probabilmente non dovrai mai calcolare questa misura a mano poiché la maggior parte dei software statistici può calcolarla per te, ma è utile conoscere la formula utilizzata dietro le quinte.

Il valore di I di Moran può variare da -1 a 1 dove:

• -1: La variabile di interesse è perfettamente dispersa
• 0: la variabile di interesse è dispersa in modo casuale
• 1: La variabile di interesse è perfettamente raggruppata

Oltre a calcolare l’I di Moran, la maggior parte dei software statistici calcola un valore p corrispondente che può essere utilizzato per determinare se i dati sono dispersi casualmente o meno.

Il test di Moran utilizza le seguenti ipotesi nulle e alternative:

Ipotesi nulla (H ₀ ): i dati sono dispersi casualmente.

Ipotesi alternativa ( _HA ): i dati non sono dispersi in modo casuale, cioè sono raggruppati in schemi visibili.

Se il valore p che corrisponde all’I di Moran è inferiore a un certo livello di significatività (cioè α = 0,05), allora possiamo rifiutare l’ipotesi nulla e concludere che i dati sono raggruppati spazialmente in modo tale che è improbabile che siano raggruppati spazialmente. avvenuto per caso.

Io di Moran: alcuni esempi

I seguenti esempi rappresentano carte false con valori diversi per l’I di Moran.

Supponiamo che ogni quadrato sulla mappa rappresenti una contea e che le contee con un reddito familiare medio superiore a 50.000 dollari siano visualizzate in blu.

I di Moran = 0: il reddito familiare medio è disperso in modo casuale (ovvero gruppi casuali in aree casuali).

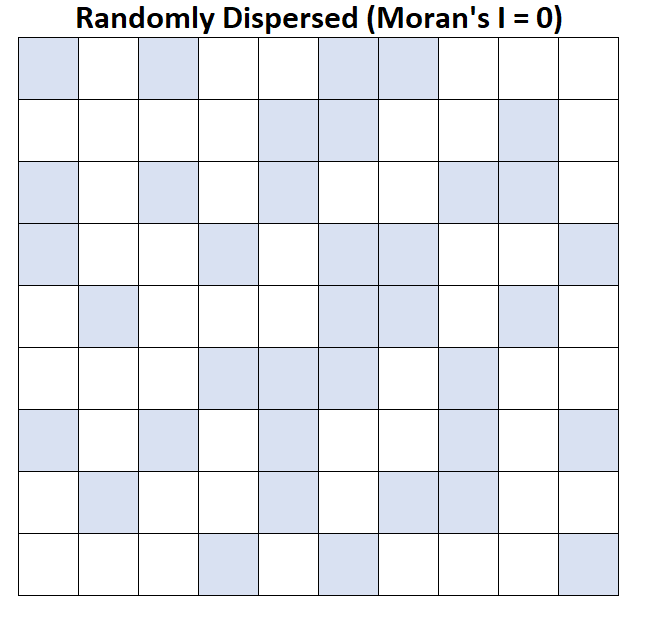
I di Moran = -1: il reddito familiare medio è perfettamente disperso.

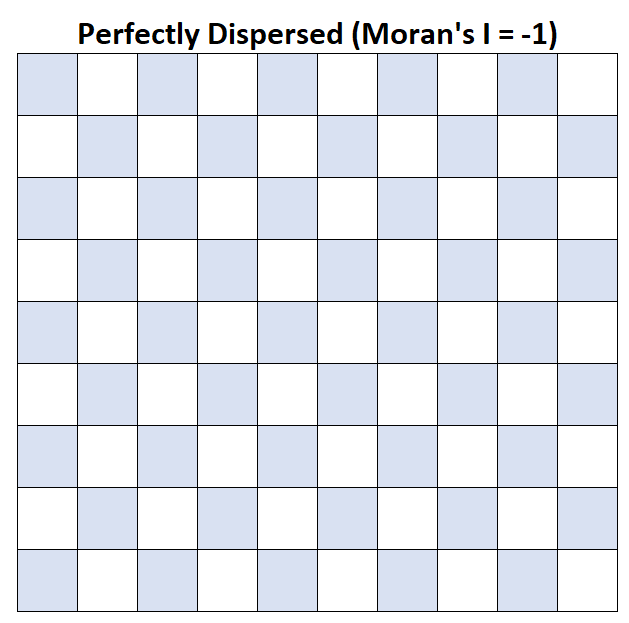
I = 1 di Moran: il reddito familiare medio è perfettamente raggruppato.

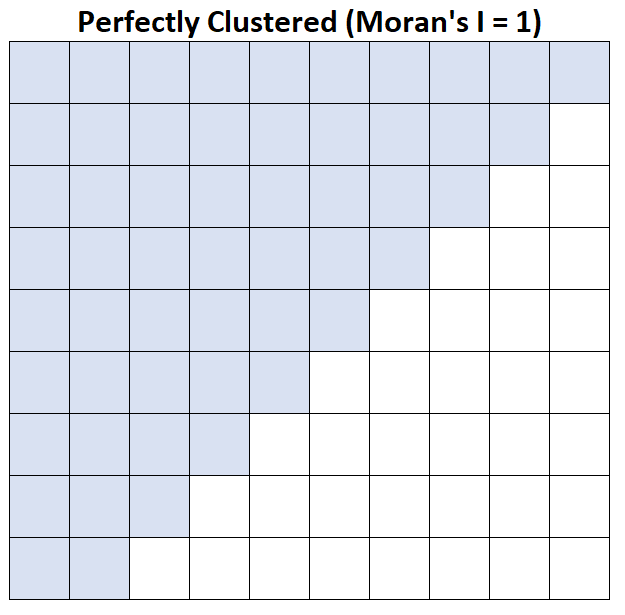
Fare riferimento a questo esempio per un esempio concreto di calcolo della I di Moran nel software statistico R.