Cos’è la multicollinearità perfetta? (definizione ed esempi)

In statistica, la multicollinearità si verifica quando due o più variabili predittive sono altamente correlate tra loro, in modo tale da non fornire informazioni univoche o indipendenti nel modello di regressione.

Se il grado di correlazione tra le variabili è sufficientemente elevato, ciò può causare problemi durante l’adattamento e l’interpretazione del modello di regressione.

Il caso più estremo di multicollinearità è chiamato multicollinearità perfetta . Ciò si verifica quando due o più variabili predittive hanno una relazione lineare esatta tra loro.

Ad esempio, supponiamo di avere il seguente set di dati:

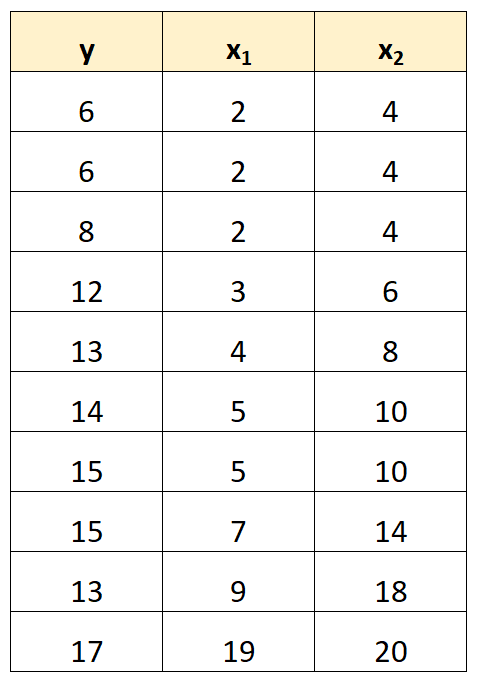
Si noti che i valori della variabile predittore x ₂ sono semplicemente i valori di x ₁ moltiplicati per 2.

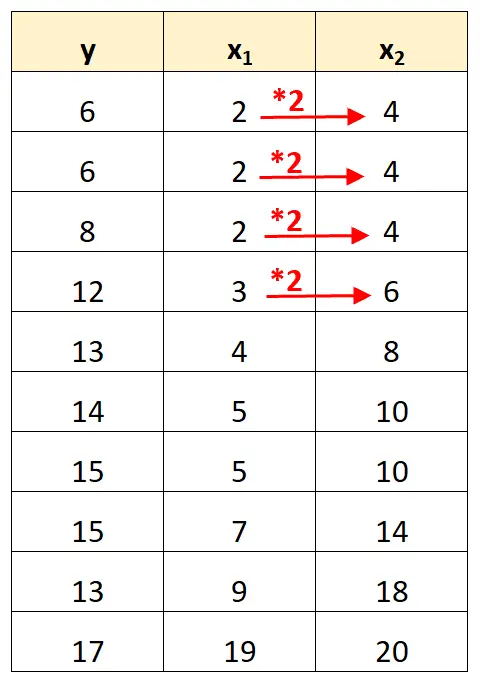
Questo è un esempio di multicollinearità perfetta .

Il problema della multicollinearità perfetta

Quando in un set di dati è presente una multicollinearità perfetta, i minimi quadrati ordinari non sono in grado di produrre stime dei coefficienti di regressione.

Infatti, non è possibile stimare l’effetto marginale di una variabile predittrice (x ₁ ) sulla variabile di risposta (y) mantenendo costante un’altra variabile predittrice (x ₂ ) perché x ₂ si muove sempre esattamente quando si muove x ₁ .

In breve, la multicollinearità perfetta rende impossibile stimare un valore per ciascun coefficiente in un modello di regressione.

Come gestire la multicollinearità perfetta

Il modo più semplice per gestire la multicollinearità perfetta è rimuovere una delle variabili che ha una relazione lineare esatta con un’altra variabile.

Ad esempio, nel nostro set di dati precedente, potremmo semplicemente rimuovere x ₂ come variabile predittrice.

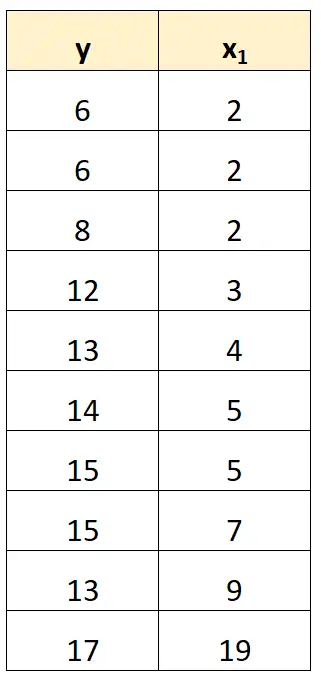
Quindi adatteremo un modello di regressione utilizzando x ₁ come variabile predittrice e y come variabile di risposta.

Esempi di multicollinearità perfetta

Gli esempi seguenti mostrano i tre scenari più comuni di perfetta multicollinearità nella pratica.

1. Una variabile predittrice è multipla di un’altra

Supponiamo di voler utilizzare “altezza in centimetri” e “altezza in metri” per prevedere il peso di una determinata specie di delfini.

Ecco come potrebbe apparire il nostro set di dati:

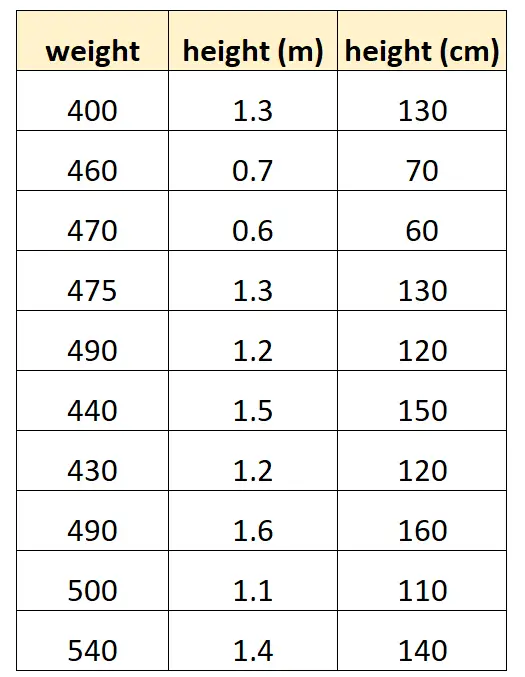
Si noti che il valore di “altezza in centimetri” è semplicemente uguale a “altezza in metri” moltiplicato per 100. Questo è un caso di multicollinearità perfetta.

Se proviamo ad adattare un modello di regressione lineare multipla in R utilizzando questo set di dati, non saremo in grado di produrre una stima del coefficiente per la variabile predittrice “metri”:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Una variabile predittrice è una versione trasformata di un’altra

Supponiamo di voler utilizzare “punti” e “punti in scala” per prevedere la valutazione dei giocatori di basket.

Supponiamo che la variabile “punti scalati” sia calcolata come:

Punti scalati = (punti – μ _punti ) / σ _punti

Ecco come potrebbe apparire il nostro set di dati:

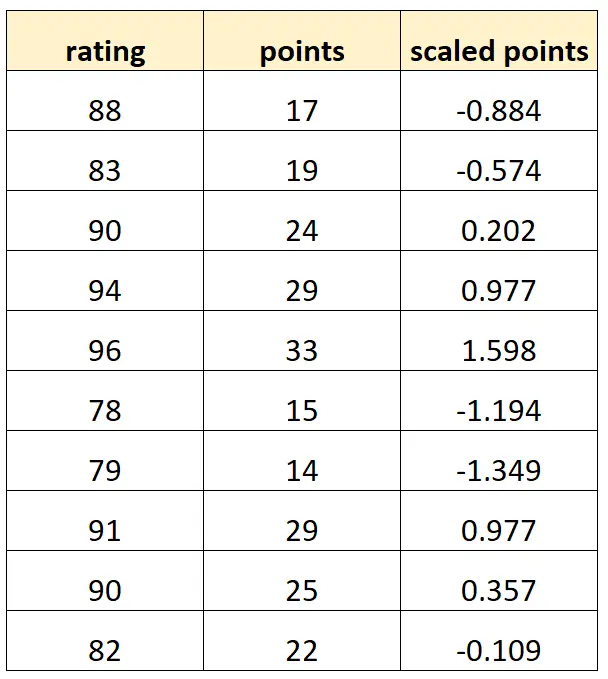
Tieni presente che ogni valore di “punti scalati” è semplicemente una versione standardizzata di “punti”. Questo è un caso di multicollinearità perfetta.

Se proviamo ad adattare un modello di regressione lineare multipla in R utilizzando questo set di dati, non saremo in grado di produrre una stima del coefficiente per la variabile predittrice “punti scalati”:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. La trappola della variabile fittizia

Un altro scenario in cui può verificarsi una perfetta multicollinearità è noto come trappola delle variabili dummy . Questo è quando vogliamo prendere una variabile categoriale in un modello di regressione e convertirla in una “variabile fittizia” che assume i valori di 0, 1, 2, ecc.

Ad esempio, supponiamo di voler utilizzare le variabili predittive “età” e “stato civile” per prevedere il reddito:

Per utilizzare lo “stato civile” come variabile predittrice, dobbiamo prima convertirlo in una variabile fittizia.

Per fare ciò, possiamo lasciare “Single” come valore di base, poiché ciò accade più spesso, e assegnare valori pari a 0 o 1 a “Sposato” e “Divorzio” come segue:

Un errore sarebbe creare tre nuove variabili dummy come segue:

In questo caso, la variabile “Single” è una perfetta combinazione lineare delle variabili “Sposato” e “Divorziato”. Questo è un esempio di multicollinearità perfetta.

Se proviamo ad adattare un modello di regressione lineare multipla in R utilizzando questo set di dati, non saremo in grado di produrre una stima dei coefficienti per ciascuna variabile predittrice:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Risorse addizionali

Una guida alla multicollinearità e al VIF nella regressione
Come calcolare il VIF in R
Come calcolare VIF in Python
Come calcolare VIF in Excel