Eventi reciprocamente inclusivi o reciprocamente esclusivi

Due eventi si escludono a vicenda se non possono verificarsi contemporaneamente.

Ad esempio, supponiamo che l’evento A sia l’evento in cui un dado esce su un numero pari e l’evento B è l’evento in cui un dado esce su un numero dispari.

Definiremo lo spazio campionario per gli eventi come segue:

• A = {2, 4, 6}
• B = {1, 3, 5}

Si noti che non vi è alcuna sovrapposizione tra i due spazi campionati. Quindi gli eventi A e B si escludono a vicenda perché non possono verificarsi entrambi contemporaneamente. Il numero su cui cade un dado non può essere sia pari che dispari.

Viceversa, due eventi sono mutualmente inclusivi se possono verificarsi contemporaneamente.

Ad esempio, supponiamo che l’evento C sia l’evento in cui un dado esce su un numero pari e che l’evento D sia l’evento in cui un dado esce su un numero maggiore di 3.

Definiremo lo spazio campionario per gli eventi come segue:

• C = {2, 4, 6}
• d = {4, 5, 6}

Si noti che esiste una sovrapposizione tra i due spazi campionati. Pertanto, gli eventi C e D sono entrambi mutualmente inclusivi perché possono verificarsi contemporaneamente. È possibile che il dado esca su un numero pari maggiore di 3.

Probabilità degli eventi

Se due eventi si escludono a vicenda , la probabilità che si verifichino entrambi è zero.

Ad esempio, considera i due spazi di esempio per gli eventi A e B sopra:

• A = {2, 4, 6}
• B = {1, 3, 5}

Poiché non c’è sovrapposizione negli spazi campionari, diremmo P(A e B) = 0 .

Ma se due eventi sono mutualmente inclusivi , allora la probabilità che si verifichino entrambi sarà un numero maggiore di zero.

Ad esempio, considera i due spazi di esempio per gli eventi C e D in precedenza:

• C = {2, 4, 6}
• d = {4, 5, 6}

Poiché ci sono 6 numeri possibili su cui i dadi potrebbero fermarsi e due di questi numeri (4 e 6) appartengono ad entrambi gli eventi C e D, calcoleremo P(C e D) come 2/6 o 1/3 .

Visualizza eventi reciprocamente inclusivi e reciprocamente esclusivi

Utilizziamo spesso i diagrammi di Venn per visualizzare le probabilità associate agli eventi.

Se due eventi si escludono a vicenda , non si sovrapporranno affatto in un diagramma di Venn:

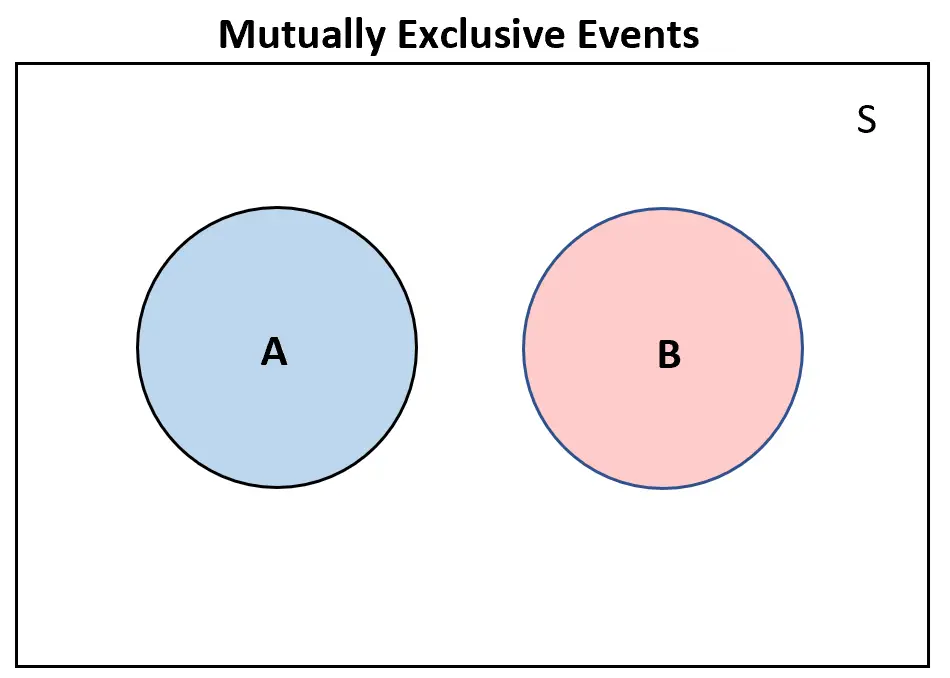
Al contrario, se due eventi sono reciprocamente inclusivi , ci sarebbe almeno qualche sovrapposizione nel diagramma di Venn:

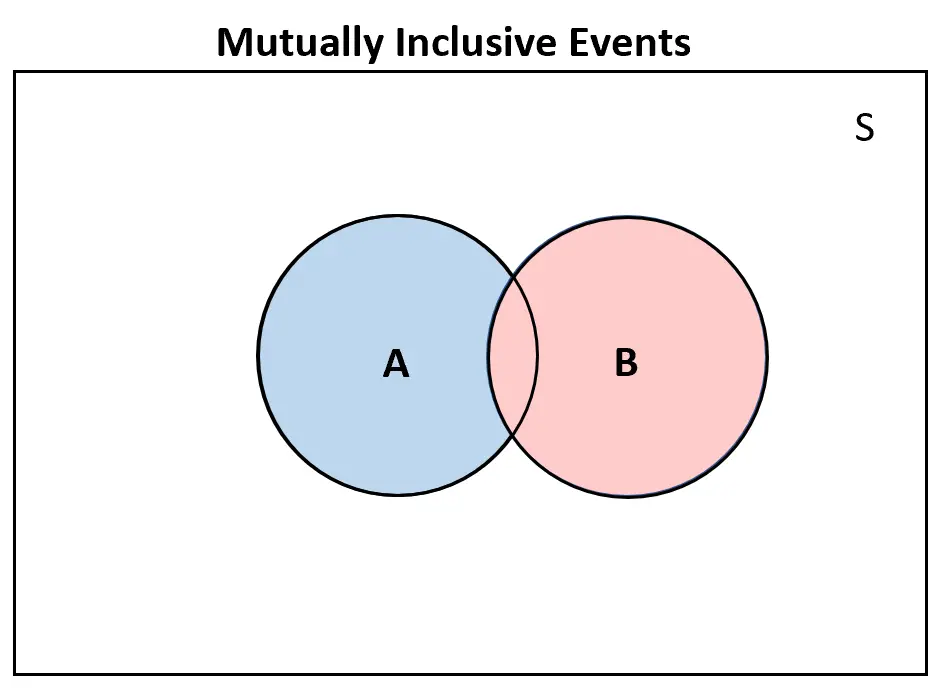
Risorse addizionali

Un’introduzione alla probabilità teorica
La regola generale della moltiplicazione
Cosa sono gli eventi disgiunti?