Variazione all'interno del gruppo o tra gruppi nell'anova
Un’ANOVA unidirezionale viene utilizzata per determinare se le medie di tre o più gruppi indipendenti sono uguali o meno.
Un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:
- H 0 : tutte le medie dei gruppi sono uguali.
- H A : Almeno una media del gruppo è diversa dalle altre.
Ogni volta che esegui un’ANOVA unidirezionale, ti ritroverai con una tabella riepilogativa simile alla seguente:
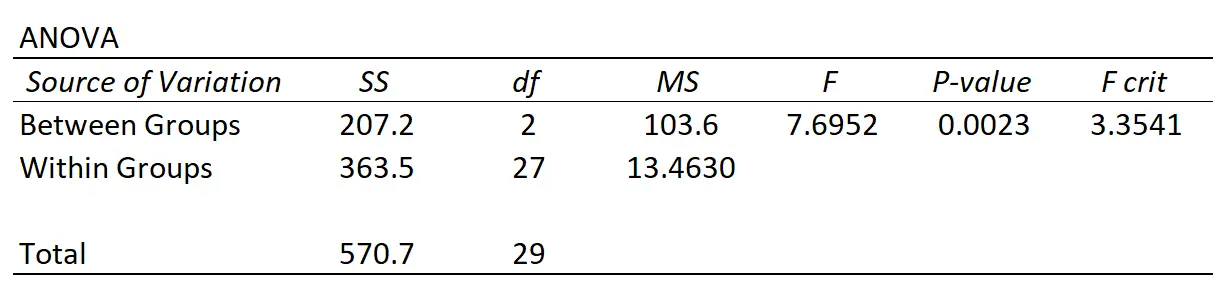
Possiamo vedere che ci sono due diverse fonti di variazione misurate da un’ANOVA:
Variazione tra gruppi : la variazione totale tra la media di ciascun gruppo e la media complessiva.
Variazione all’interno del gruppo : la variazione totale dei valori individuali in ciascun gruppo e la media del loro gruppo.
Se la variazione tra i gruppi è elevata rispetto alla variazione all’interno del gruppo, allora la statistica F dell’ANOVA sarà più alta e il corrispondente valore p sarà più basso, rendendo più probabile che venga rifiutata l’ipotesi nulla secondo la quale le medie del gruppo sono uguali.
L’esempio seguente mostra come calcolare nella pratica la variazione tra gruppi e la variazione all’interno del gruppo per l’ANOVA unidirezionale.
Esempio: calcolo della variazione all’interno di un gruppo e tra gruppi in ANOVA
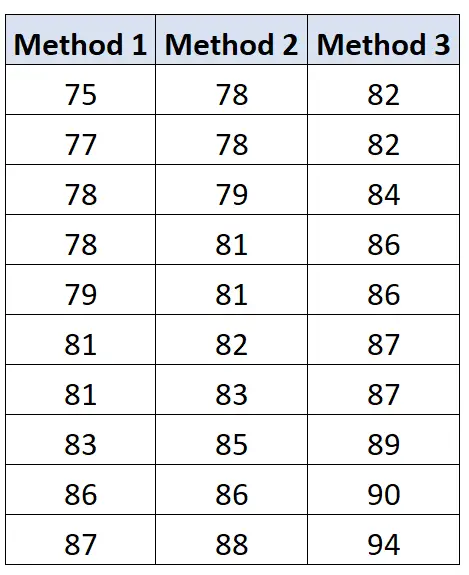
Supponiamo di voler determinare se tre diversi metodi di studio portano a punteggi medi degli esami diversi. Per testarlo, reclutiamo 30 studenti e ne assegniamo casualmente 10 ciascuno a utilizzare un metodo di studio diverso.
Di seguito sono riportati i risultati degli esami degli studenti di ciascun gruppo:
Possiamo usare la seguente formula per calcolare la variazione tra i gruppi :
Variazione tra gruppi = Σn j (X j – X ..) 2
Oro:
- n j : la dimensione del campione del gruppo j
- Σ : un simbolo che significa “somma”
- X j : la media del gruppo j
- X .. : la media complessiva
Per calcolare questo valore, calcoleremo prima la media di ciascun gruppo e la media complessiva:
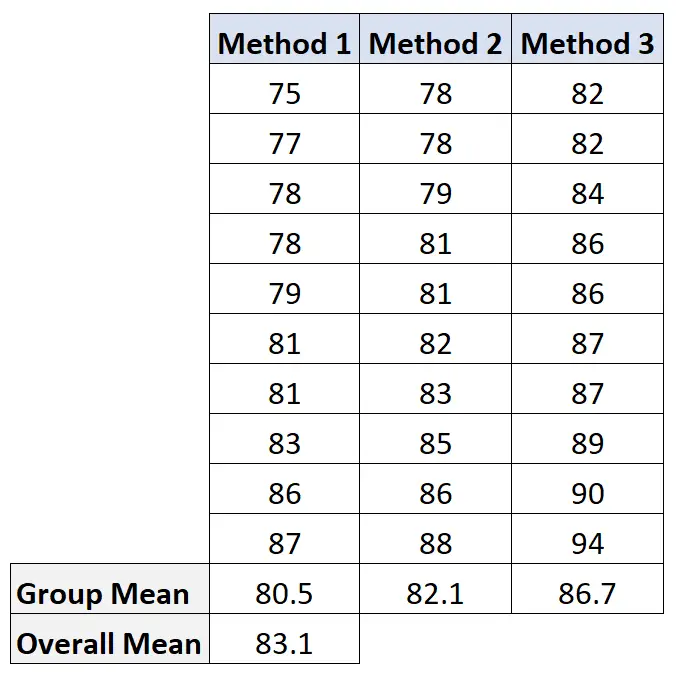
Quindi calcoliamo la variazione tra i gruppi come segue: 10(80.5-83.1) 2 + 10(82.1-83.1) 2 + 10(86.7-83.1) 2 = 207.2 .
Quindi possiamo utilizzare la seguente formula per calcolare la variazione all’interno del gruppo :
Variazione intragruppo : Σ(X ij – X j ) 2
Oro:
- Σ : un simbolo che significa “somma”
- X ij : l’ iesima osservazione del gruppo j
- X j : la media del gruppo j
Nel nostro esempio, calcoliamo la variazione all’interno del gruppo come:
Gruppo 1: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2+ (78-80,5) 2+ (79-80,5) 2+ (81-80,5) 2+ (81-80,5) 2+ (83-80,5) 2+ (86-80,5) 2+ (87-80,5) 2 = 136,5
Gruppo 2: (78-82.1) 2 + (78-82.1) 2 + (79-82.1) 2+ (81-82.1) 2+ (81-82.1) 2+ (82-82.1) 2+ (83-82.1) 2+ (85-82.1) 2+ (86-82.1) 2+ (88-82,1) 2 = 104,9
Gruppo 3: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2+ (86-86,7) 2+ (86-86,7) 2+ (87-86,7) 2+ (87-86,7) 2+ (89-86,7) 2+ (90-86,7) 2+ (94-86,7) 2 = 122,1
Variazione all’interno del gruppo: 136,5 + 104,9 + 122,1 = 363,5
Se utilizziamo un software statistico per eseguire un’ANOVA unidirezionale utilizzando questo set di dati, otterremo la seguente tabella ANOVA:
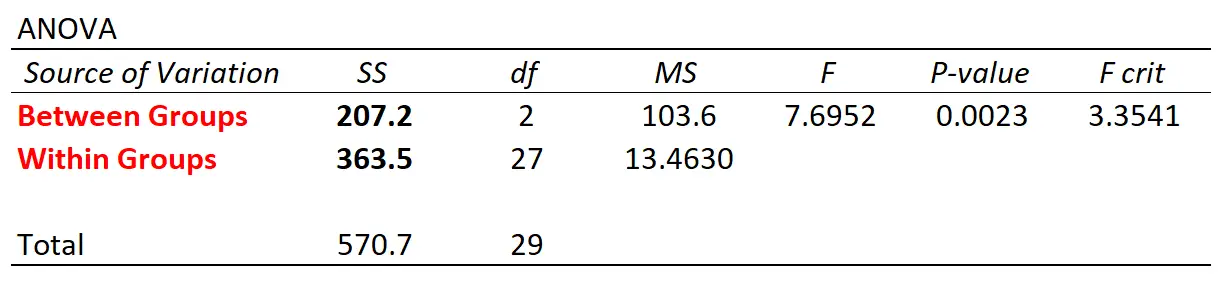
Si noti che i valori di variazione tra gruppi e all’interno del gruppo corrispondono a quelli calcolati manualmente.
La statistica F complessiva nella tabella è un modo per quantificare la relazione tra la variazione tra i gruppi e la variazione all’interno del gruppo.
Maggiore è la statistica F, maggiore è la variazione tra i gruppi rispetto alla variazione all’interno dei gruppi.
Pertanto, quanto più ampia è la statistica F, tanto più evidente è la differenza tra le medie del gruppo.
Possiamo vedere in questo esempio che il valore p che corrisponde a una statistica F di 7.6952 è .0023 .
Poiché questo valore è inferiore a α = 0,05, rifiutiamo l’ipotesi nulla dell’ANOVA e concludiamo che le tre tecniche di studio non portano allo stesso punteggio all’esame.
Risorse addizionali
Le seguenti esercitazioni forniscono informazioni aggiuntive sui modelli ANOVA:
Introduzione all’ANOVA unidirezionale
Come interpretare il valore F e il valore P in ANOVA
La guida completa: come riportare i risultati ANOVA
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più