Odds ratio e rischio relativo: qual è la differenza?

Due termini che gli studenti spesso confondono in statistica sono odds ratio e rischio relativo .

Usiamo spesso queste due metriche quando analizziamo una tabella 2 per 2, che assume il seguente formato:

L’ odds ratio ci dice il rapporto tra la probabilità che un evento si verifichi in un gruppo di trattamento e la probabilità che un evento si verifichi in un gruppo di controllo. Viene calcolato come segue:

Rapporto di probabilità = (A*D) / (B*C)

Il rischio relativo è il rapporto tra la probabilità che un evento si verifichi in un gruppo di trattamento e la probabilità che un evento si verifichi in un gruppo di controllo. Viene calcolato come segue:

Rischio relativo = [A/(A+B)] / [C/(C+D)]

In breve, ecco la differenza:

• Un rapporto di probabilità è un rapporto di due probabilità .
• Il rischio relativo è un rapporto di due probabilità .

L’esempio seguente mostra come calcolare e interpretare un odds ratio e il rischio relativo in una situazione reale.

Esempio: calcolo dell’odds ratio e del rischio relativo

Si presuppone che 100 giocatori di basket utilizzino un nuovo programma di allenamento e 100 giocatori utilizzino un vecchio programma di allenamento. Alla fine del programma, testiamo ogni giocatore per vedere se supera un determinato test di abilità.

La tabella seguente mostra il numero di giocatori che hanno superato e fallito, in base al programma utilizzato:

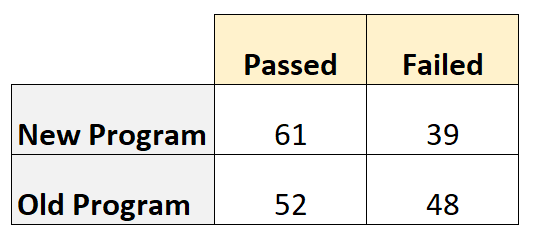
Il rapporto odd è calcolato come segue:

• Rapporto di probabilità = (A*D) / (B*C)
• Rapporto di probabilità = (61*48) / (39*52)
• Rapporto di probabilità = 1,44

Interpreteremmo questo nel senso che le probabilità che un giocatore superi il test utilizzando il nuovo programma sono 1,44 volte superiori alle probabilità che un giocatore superi il test utilizzando il vecchio programma.

In altre parole, le possibilità che un giocatore superi il test aumentano attraverso l’utilizzo del nuovo programma.

Il rischio relativo è calcolato come

• Rischio relativo = [A/(A+B)] / [C/(C+D)]
• Rischio relativo = [61/(61+39)] / [52/(52+48)]
• Rischio relativo = 1,17

Interpreteremmo questo nel senso che il rapporto tra la probabilità che un giocatore superi il test utilizzando il nuovo programma e il vecchio programma è 1,17 .

Poiché questo valore è maggiore di 1, ciò ci dice che la probabilità di successo è maggiore nel nuovo programma che nel vecchio programma.

Possiamo vederlo anche calcolando direttamente la probabilità che un giocatore passi sotto ciascun programma:

Probabilità di successo con il nuovo programma = 61/100 = 61%

Probabilità di successo con il vecchio programma = 52/100 = 52%

Prendendo il rapporto tra queste probabilità, possiamo calcolare il rischio relativo come 61% / 52% = 1,17 .

Si noti che l’odds ratio e il rischio relativo sono entrambi maggiori di 1, il che ci dice che le possibilità di sperimentare un evento (ad esempio superare il test di abilità) sono maggiori nel gruppo di trattamento che nel gruppo di controllo.

L’odds ratio e il rischio relativo ci forniscono informazioni simili, ma interpretiamo ciascun valore in modo leggermente diverso.

Particolarmente:

• L’ odds ratio ci dice che le possibilità di superare il test di abilità sono più elevate con il nuovo programma.
• Il rischio relativo ci dice che la probabilità di superare il test di abilità è più alta con il nuovo programma.

Utilizzando entrambi i parametri, possiamo facilmente vedere che il nuovo programma è migliore di quello vecchio.

Risorse addizionali

I seguenti tutorial offrono ulteriori informazioni sui rapporti di probabilità e sul rischio relativo:

Come interpretare i rapporti di probabilità
Come interpretare il rischio relativo
Come calcolare il rapporto quote e il rischio relativo in Excel