Operazioni sugli insiemi: unione, intersezione, complemento e differenza

Un insieme è una raccolta di elementi.

Designiamo un insieme con una lettera maiuscola e definiamo gli elementi dell’insieme utilizzando le parentesi graffe. Ad esempio, supponiamo di avere un insieme chiamato “A” con gli elementi 1, 2, 3. Lo scriveremo come segue:

A = {1, 2, 3}

Questo tutorial spiega le operazioni sugli insiemi più comunemente utilizzate in probabilità e statistica.

unione

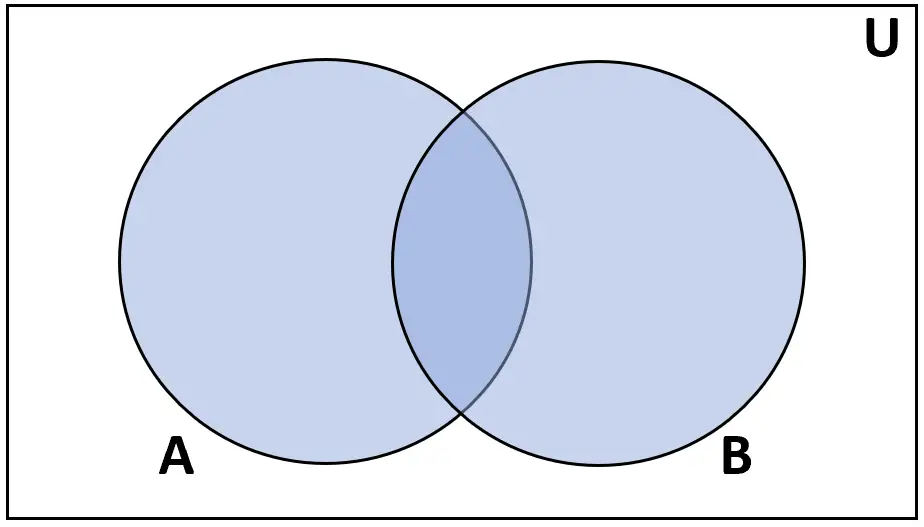
Definizione: L’ unione degli insiemi A e B è l’insieme degli elementi che si trovano in A o in B.

Voto: A ∪ B

Esempi:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Intersezione

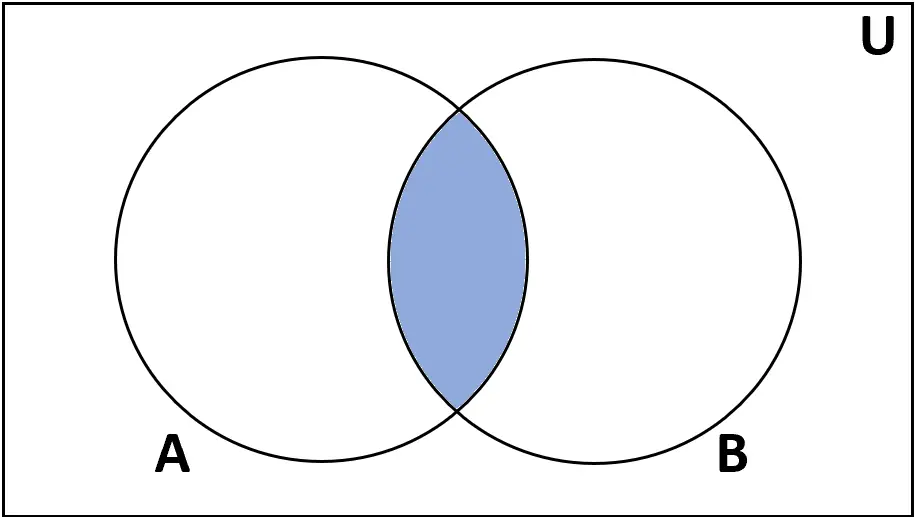
Definizione: l’ intersezione degli insiemi A e B è l’insieme degli elementi che si trovano sia in A che in B.

Notazione: A ∩ B

Esempi:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Complemento

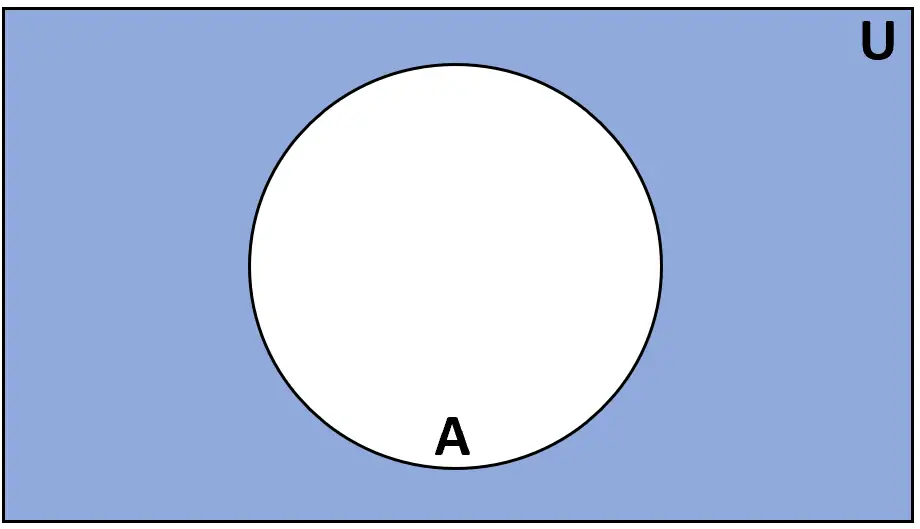
Definizione: Il complemento dell’insieme A è l’insieme degli elementi che appartengono all’insieme universale U ma non appartengono ad A.

Voto: A’ o ^Ac

Esempi:

• Se U = {1, 2, 3, 4, 5, 6} e A = {1, 2}, allora A ^c = {3, 4, 5, 6}
• Se U = {1, 2, 3} e A = {1, 2}, allora A ^c = {3}

Differenza

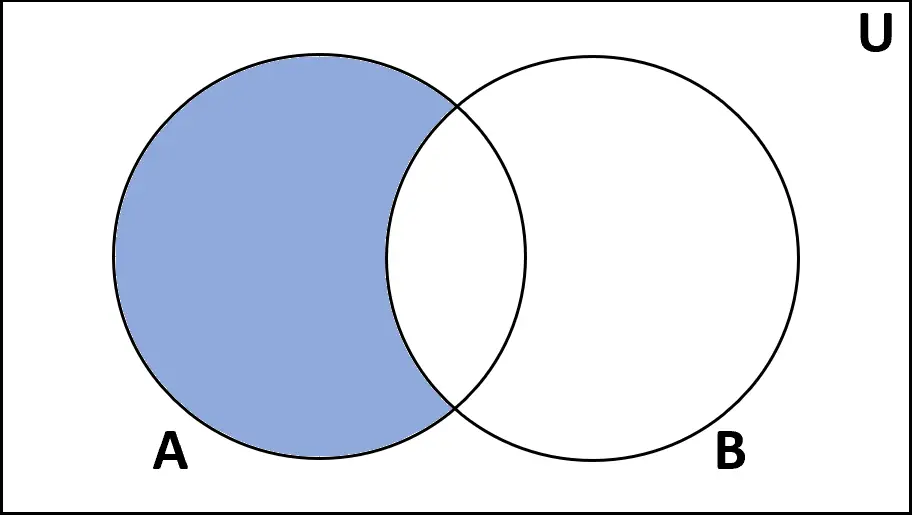
Definizione: la differenza tra gli insiemi A e B è l’insieme degli elementi che si trovano in A ma non in B.

Valutazioni: A-B

Esempi:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Differenza simmetrica

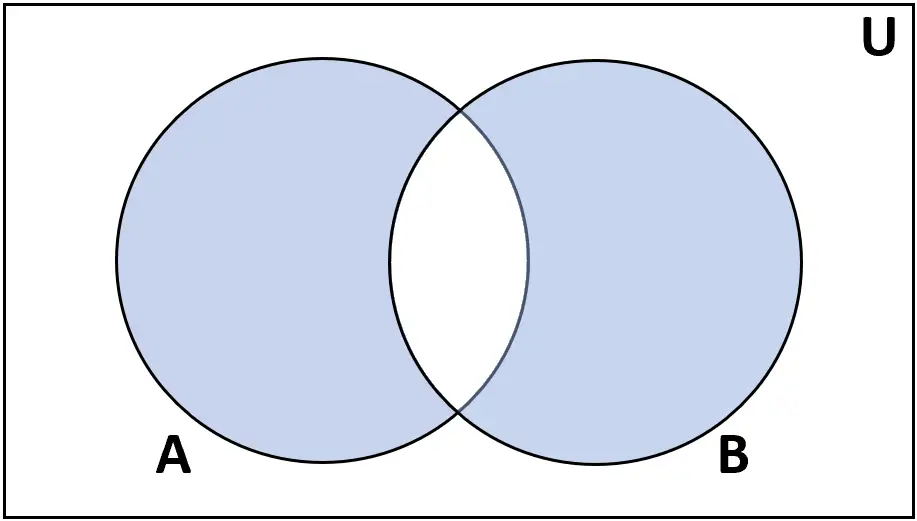
Definizione: la differenza simmetrica degli insiemi A e B è l’insieme degli elementi che si trovano in A o B, ma non in entrambi.

Valutazione: AΔB

Esempi:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

prodotto cartesiano

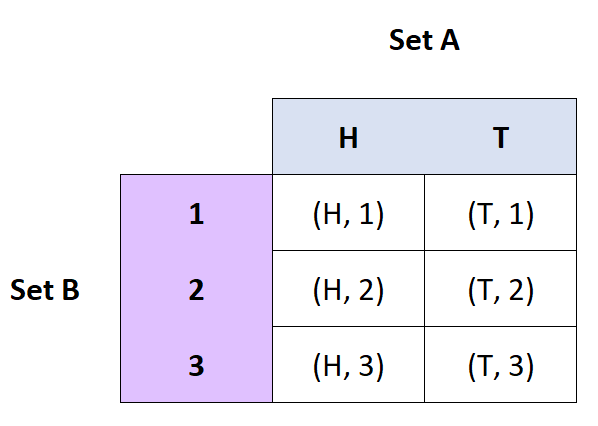
Definizione: Il prodotto cartesiano degli insiemi A e B è l’insieme delle coppie ordinate di A e B.

Voto: AxB

Esempi:

• Se A = {H, T} e B = {1, 2, 3}, allora A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Se A = {T, H} e B = {1, 2, 3}, allora A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}