L’intervallo interquartile (iqr) è influenzato da valori anomali?

Nelle statistiche, spesso vogliamo sapere quanto sono “distribuiti” i valori in una distribuzione.

Un modo diffuso per misurare la diffusione è l’intervallo interquartile , che viene calcolato come la differenza tra il primo quartile e il terzo quartile di un set di dati. I quartili sono semplicemente valori che dividono un set di dati in quattro parti uguali.

Esempio: Calcolo dell’intervallo interquartile

L’esempio seguente mostra come calcolare l’intervallo interquartile per un determinato set di dati:

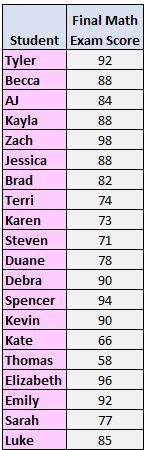
Passaggio 1: disporre i valori dal più piccolo al più grande.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Trova la mediana.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

In questo caso, la mediana è compresa tra 85 e 88.

3. La mediana divide il set di dati in due metà. La mediana della metà inferiore è il quartile inferiore e la mediana della metà superiore è il quartile superiore:

58, 66, 71, 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Calcola l’intervallo interquartile.

In questo caso, il primo quartile è la media dei due valori centrali nella metà inferiore del set di dati (75,5) e il terzo quartile è la media dei due valori centrali nella metà superiore dei dati set (91).

Quindi l’intervallo interquartile è 91 – 75,5 = 15,5

L’intervallo interquartile non è influenzato dai valori anomali

Uno dei motivi per cui le persone preferiscono utilizzare l’intervallo interquartile (IQR) quando calcolano la “diffusione” di un set di dati è che è resistente ai valori anomali. Poiché l’IQR rappresenta semplicemente l’intervallo medio del 50% dei valori dei dati, non è influenzato da valori anomali estremi .

Per dimostrarlo, consideriamo il seguente set di dati:

[1, 4, 8, 11, 13, 17, 17, 20]

Ecco le diverse metriche di propagazione per questo set di dati:

• Intervallo interquartile: 11
• Portata: 19
• Deviazione standard: 6,26
• Differenza: 39,23

Consideriamo ora lo stesso set di dati ma con l’aggiunta di un valore anomalo estremo:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Ecco le diverse metriche di propagazione per questo set di dati:

• Intervallo interquartile: 12,5
• Gamma: 149
• Deviazione standard: 43,96
• Spread: 1.932,84

Nota come l’intervallo interquartile cambia solo leggermente, da 11 a 12,5. Tuttavia, tutte le altre misure di dispersione cambiano radicalmente.

Ciò dimostra che l’intervallo interquartile non è influenzato da valori anomali come altre misure di dispersione. Per questo motivo è un modo affidabile per misurare la distribuzione del 50% medio dei valori in qualsiasi distribuzione.

Ulteriori letture:

Misure di dispersione
Calcolatore dell’intervallo interquartile