Cos'è l'overfitting nell'apprendimento automatico? (spiegazione ed esempi)

Nell’apprendimento automatico, spesso costruiamo modelli in modo da poter fare previsioni accurate su determinati fenomeni.

Ad esempio, supponiamo di voler creare un modello di regressione che utilizzi la variabile predittrice ore trascorse a studiare per prevedere il punteggio ACT della variabile di risposta per gli studenti delle scuole superiori.

Per costruire questo modello, raccoglieremo dati sulle ore trascorse a studiare e il corrispondente punteggio ACT per centinaia di studenti in un determinato distretto scolastico.

Utilizzeremo quindi questi dati per addestrare un modello in grado di fare previsioni sul punteggio che un determinato studente riceverà in base al numero totale di ore studiate.

Per valutare l’utilità del modello, possiamo misurare quanto bene le previsioni del modello corrispondono ai dati osservati. Uno dei parametri più comunemente utilizzati per farlo è l’errore quadratico medio (MSE), che viene calcolato come segue:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Oro:

• n: numero totale di osservazioni
• y _i : il valore di risposta dell’i ^-esima osservazione
• f( _xi ): Il valore di risposta previsto dell’i- ^esima osservazione

Più le previsioni del modello si avvicinano alle osservazioni, più basso sarà il MSE.

Tuttavia, uno dei più grandi errori commessi nell’apprendimento automatico è l’ottimizzazione dei modelli per ridurre l’MSE di addestramento , ovvero la corrispondenza tra le previsioni del modello e i dati utilizzati per addestrare il modello.

Quando un modello si concentra troppo sulla riduzione dell’MSE di addestramento, spesso lavora troppo duramente per trovare modelli nei dati di addestramento che sono semplicemente causati dal caso. Quindi, quando il modello viene applicato a dati invisibili, le sue prestazioni sono scarse.

Questo fenomeno è noto come overfitting . Ciò accade quando “adattiamo” un modello troppo fedelmente ai dati di addestramento e quindi finiamo per costruire un modello che non è utile per fare previsioni sui nuovi dati.

Esempio di overfitting

Per comprendere l’overfitting, torniamo all’esempio della creazione di un modello di regressione che utilizza le ore trascorse a studiare per prevedere il punteggio ACT .

Supponiamo di raccogliere dati per 100 studenti in un determinato distretto scolastico e di creare un rapido grafico a dispersione per visualizzare la relazione tra le due variabili:

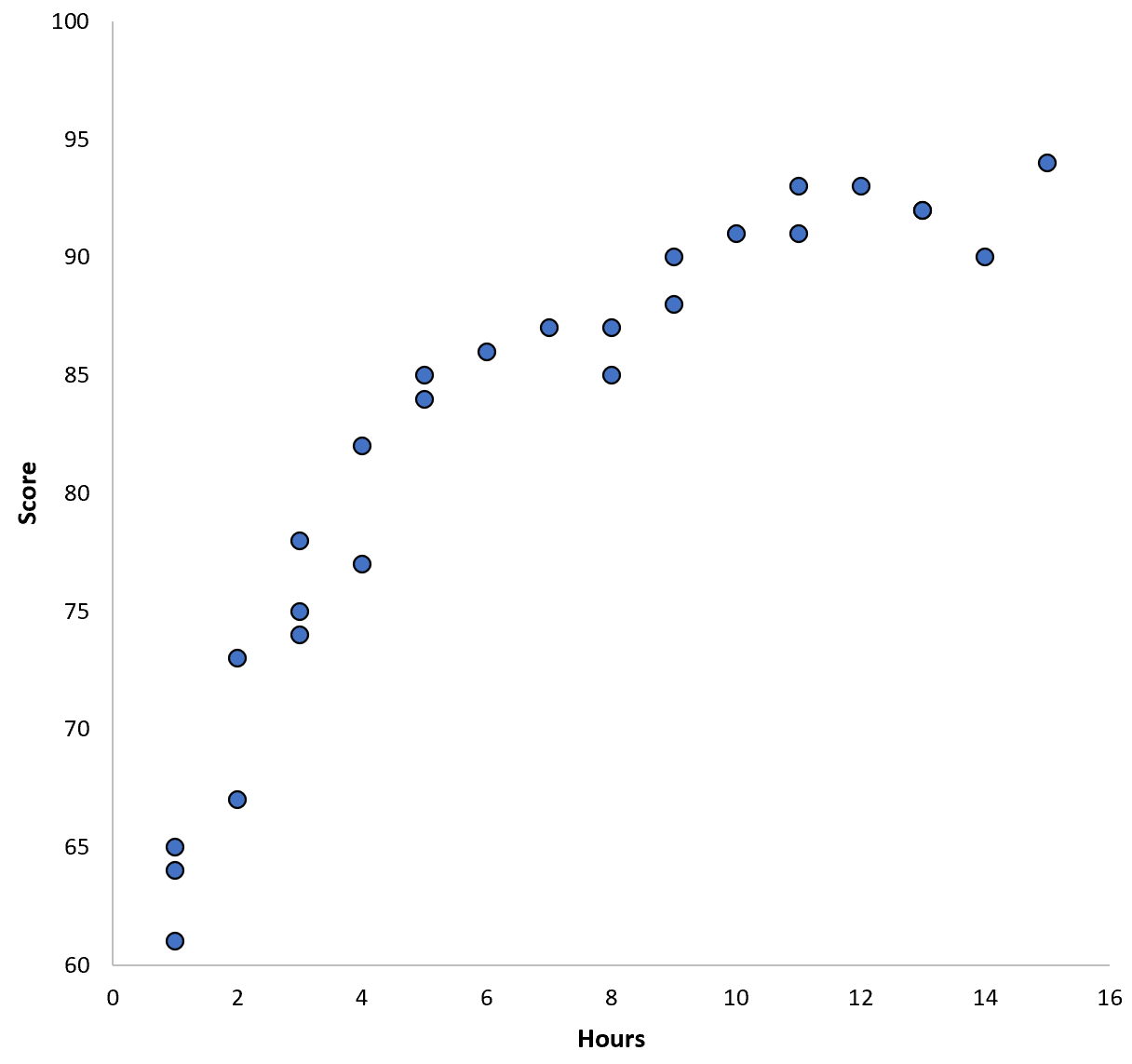
La relazione tra le due variabili sembra essere quadratica, quindi supponiamo di applicare il seguente modello di regressione quadratica:

Punteggio = 60,1 + 5,4*(Ore) – 0,2*(Ore) ²

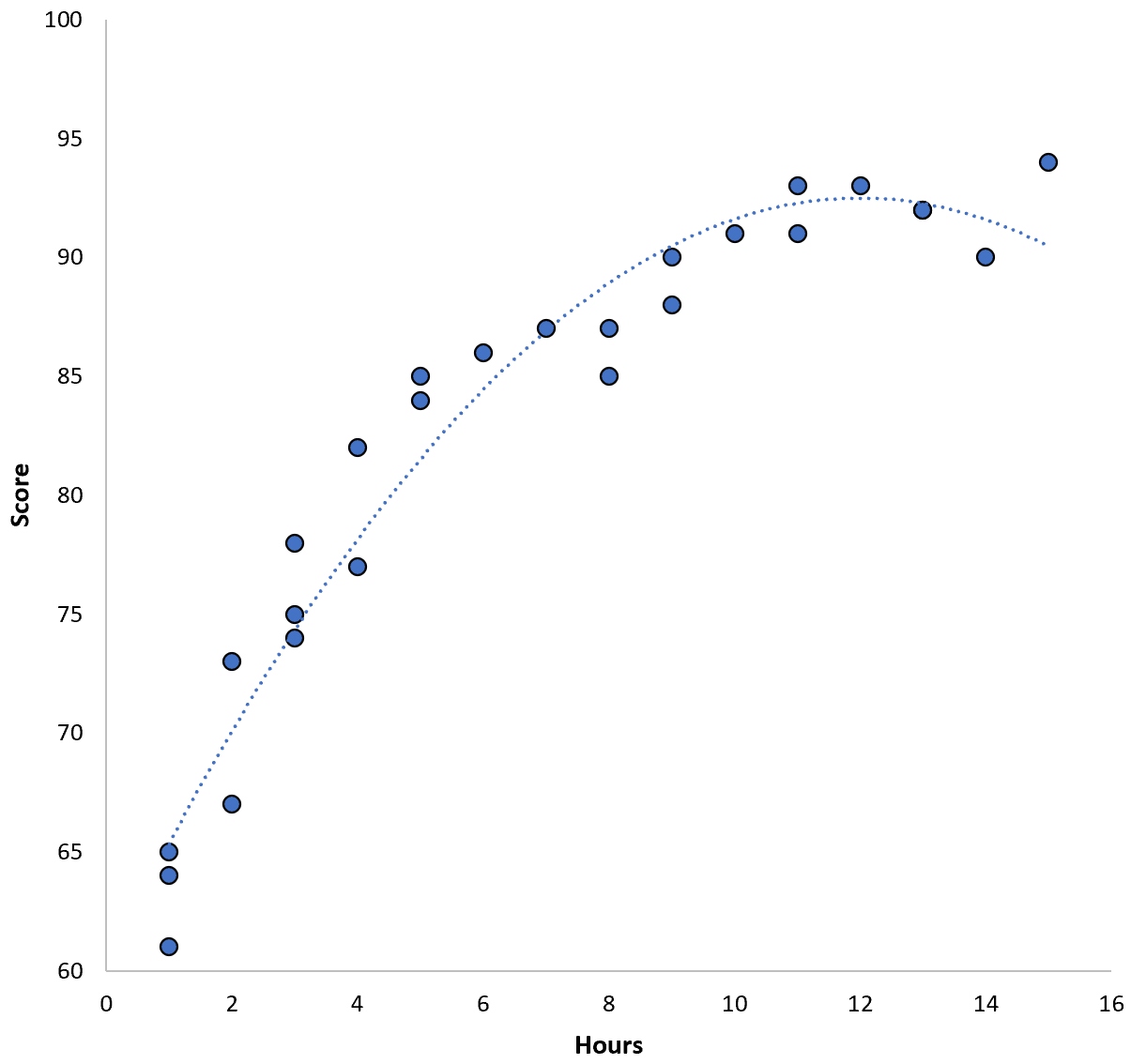
Questo modello ha un errore quadratico medio di addestramento (MSE) di 3,45 . Cioè, la differenza quadratica media tra le previsioni fatte dal modello e i punteggi ACT effettivi è 3,45.

Tuttavia, potremmo ridurre questo MSE di formazione adattando un modello polinomiale di ordine superiore. Supponiamo ad esempio di applicare il seguente modello:

Punteggio = 64,3 – 7,1*(Ore) + 8,1*(Ore) ² – 2,1*(Ore) ³ + 0,2*(Ore ^{) 4 – 0,1*(Ore) 5 +} 0,2(Ore) ⁶

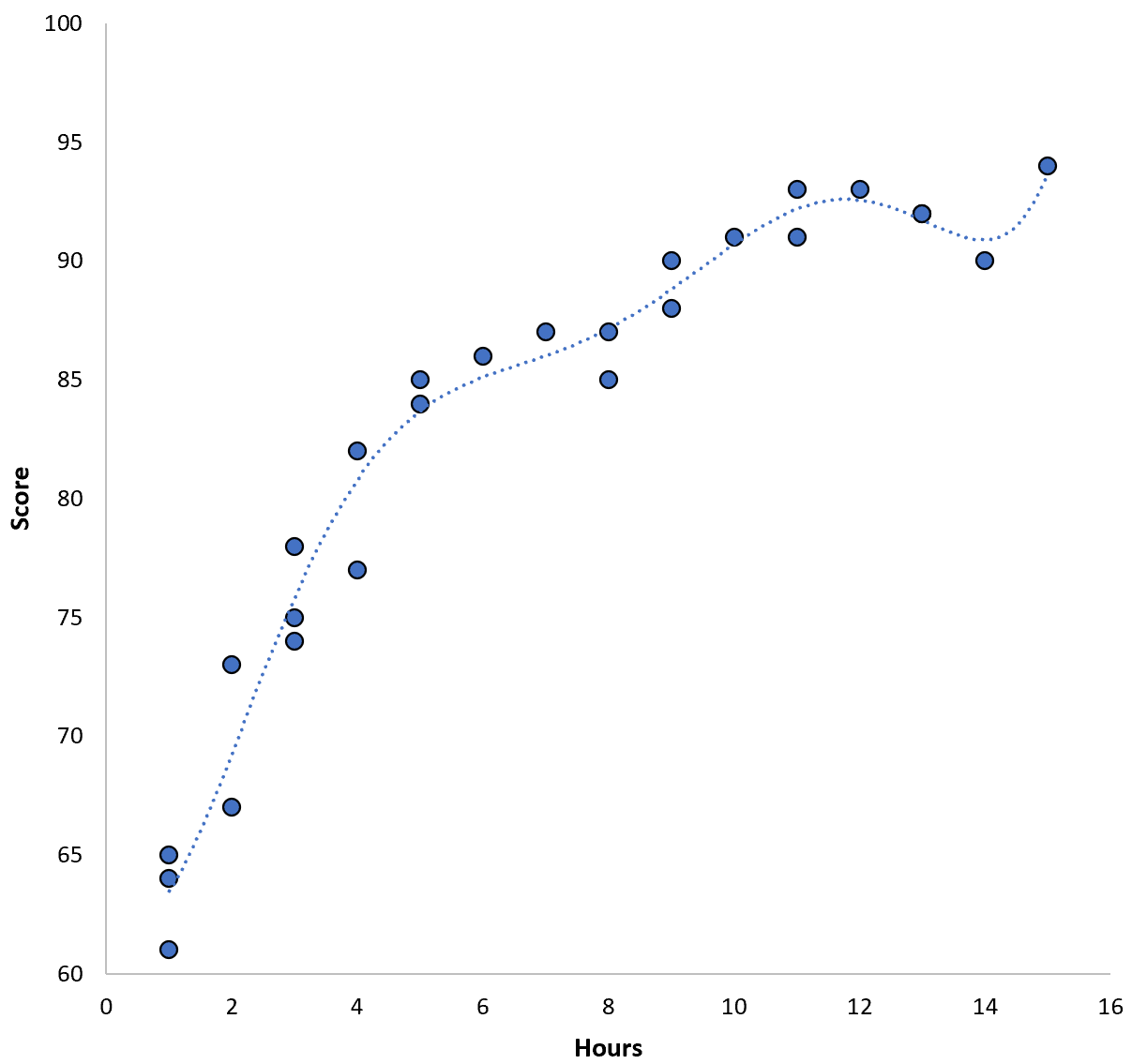
Nota come la linea di regressione si adatta molto più fedelmente ai dati effettivi rispetto alla linea di regressione precedente.

Questo modello ha un errore quadratico medio di addestramento (MSE) di soli 0,89 . Cioè, la differenza quadratica media tra le previsioni fatte dal modello e i punteggi ACT effettivi è 0,89.

Questa formazione MSE è molto più piccola di quella prodotta dal modello precedente.

Tuttavia, non ci interessa veramente l’ MSE di addestramento , ovvero quanto bene le previsioni del modello corrispondono ai dati che abbiamo utilizzato per addestrare il modello. Invece, ci preoccupiamo principalmente del test MSE : l’MSE quando il nostro modello viene applicato a dati invisibili.

Se applicassimo il modello di regressione polinomiale di ordine superiore sopra a un set di dati invisibile, probabilmente otterrebbe risultati peggiori rispetto al modello di regressione quadratica più semplice. Ciò produrrebbe cioè un test MSE più elevato, che è esattamente ciò che non vogliamo.

Come rilevare ed evitare l’overfitting

Il modo più semplice per rilevare l’overfitting è eseguire la convalida incrociata. Il metodo più comunemente utilizzato è noto come convalida incrociata k-fold e funziona come segue:

Passaggio 1: dividere casualmente un set di dati in k gruppi, o “pieghe”, di dimensioni approssimativamente uguali.

Passaggio 2: scegli una delle pieghe come set di attesa. Adatta il modello alle restanti pieghe k-1. Calcolare il test MSE sulle osservazioni nello strato che è stato tensionato.

Passaggio 3: ripetere questo processo k volte, ogni volta utilizzando un set diverso come set di esclusione.

Passaggio 4: calcolare l’MSE complessivo del test come media dei k MSE del test.

Prova MSE = (1/k)*ΣMSE _i

Oro:

• k: numero di pieghe
• MSE _i : testa MSE all’i ^-esima iterazione

Questo test MSE ci dà una buona idea di come si comporterà un determinato modello su dati sconosciuti.

In pratica, possiamo adattare diversi modelli diversi ed eseguire una convalida incrociata k-fold su ciascun modello per scoprirne il test MSE. Possiamo quindi scegliere il modello con il test MSE più basso come modello migliore da utilizzare per fare previsioni future.

Ciò garantisce la selezione di un modello che probabilmente offrirà le migliori prestazioni sui dati futuri, al contrario di un modello che semplicemente riduce al minimo l’MSE di formazione e si “adatta” bene ai dati storici.

Risorse addizionali

Qual è il compromesso tra bias e varianza nel machine learning?
Un’introduzione alla convalida incrociata K-Fold
Modelli di regressione e classificazione nell’apprendimento automatico