Perché le statistiche sono importanti? (10 motivi per cui le statistiche sono importanti!)

Il campo della statistica riguarda la raccolta, l’analisi, l’interpretazione e la presentazione dei dati.

Man mano che la tecnologia diventa sempre più presente nella nostra vita quotidiana, vengono generati e raccolti più dati che mai nella storia umana.

La statistica è l’area che può aiutarci a capire come utilizzare questi dati per eseguire le seguenti attività:

• Comprendere meglio il mondo che ci circonda.
• Prendi decisioni utilizzando i dati.
• Fare previsioni sul futuro utilizzando i dati.

In questo articolo condividiamo 10 ragioni per cui il campo della statistica è così importante nella vita moderna.

Motivo 1: utilizzare le statistiche descrittive per comprendere il mondo

Le statistiche descrittive vengono utilizzate per descrivere un dato grezzo. Esistono tre tipi principali di statistiche descrittive:

• Statistiche riassuntive
• Grafica
• le tavole

Ciascuno di questi elementi può aiutarci a comprendere meglio i dati esistenti.

Ad esempio, supponiamo di avere un set di dati grezzi che mostra i punteggi dei test di 10.000 studenti in una determinata città. Possiamo utilizzare le statistiche descrittive per:

• Calcolare il punteggio medio del test e la deviazione standard dei risultati del test.
• Genera un istogramma o un boxplot per visualizzare la distribuzione dei risultati del test.
• Creare una tabella di frequenza per comprendere la distribuzione dei risultati dei test.

Utilizzando la statistica descrittiva, possiamo comprendere i punteggi dei test degli studenti molto più facilmente che guardando semplicemente i dati grezzi.

Motivo 2: attenzione alla grafica fuorviante

Sempre più elementi grafici vengono generati in giornali, media, articoli online e riviste. Sfortunatamente, i grafici possono spesso essere fuorvianti se non si comprendono i dati sottostanti.

Ad esempio, supponiamo che una rivista pubblichi uno studio che trova una correlazione negativa tra i punteggi GPA e ACT degli studenti di una determinata università.

Tuttavia, questa correlazione negativa si verifica solo perché gli studenti che hanno sia un punteggio GPA che ACT elevato sono in grado di frequentare un’università d’élite, mentre gli studenti che hanno sia un punteggio GPA che ACT basso non sono ammessi affatto.

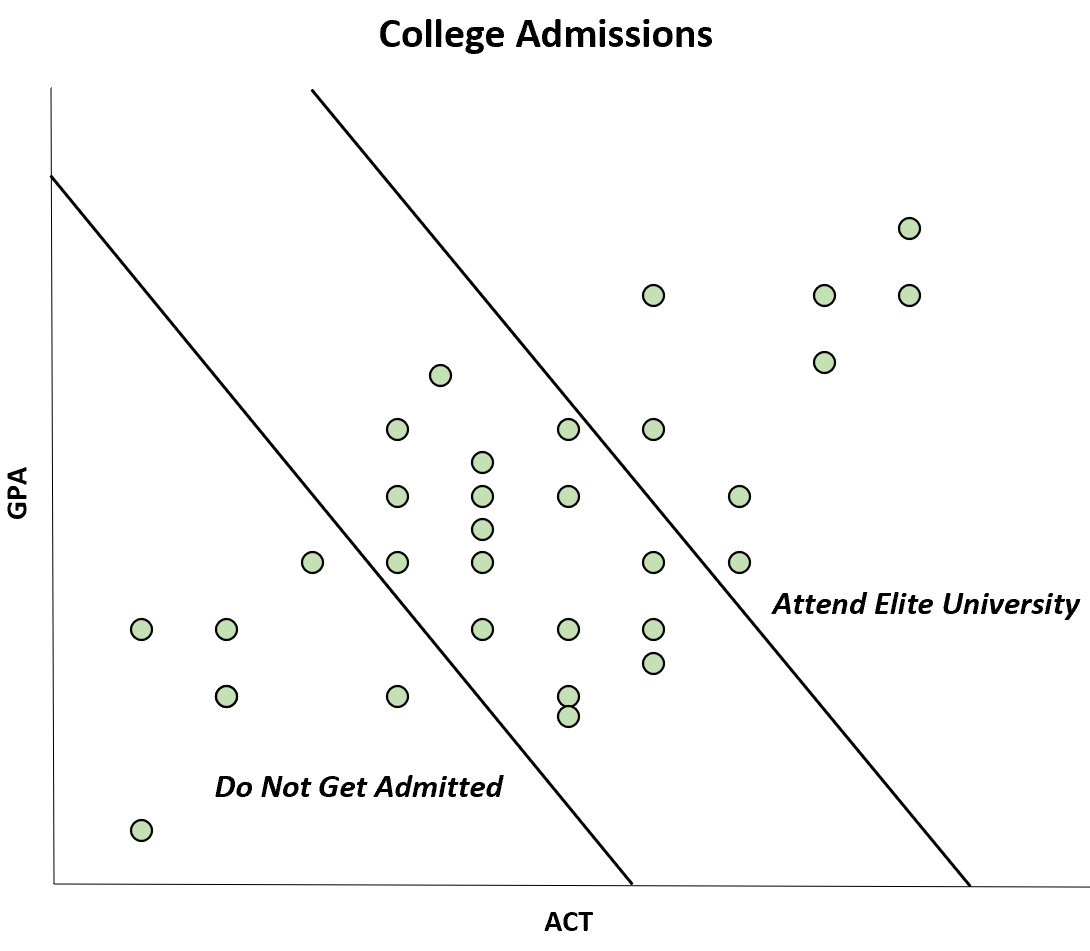
Sebbene la correlazione tra ACT e GPA sia positiva nella popolazione, la correlazione appare negativa nel campione.

Questo particolare pregiudizio è noto come pregiudizio di Berkson . Essendo consapevoli di questo pregiudizio, puoi evitare di essere fuorviato da alcuni grafici.

Motivo 3: diffidare delle variabili confuse

Un concetto importante che imparerai in statistica è il concetto di variabili confuse .

Si tratta di variabili che non vengono prese in considerazione e che possono confondere i risultati di un esperimento e portare a conclusioni inaffidabili.

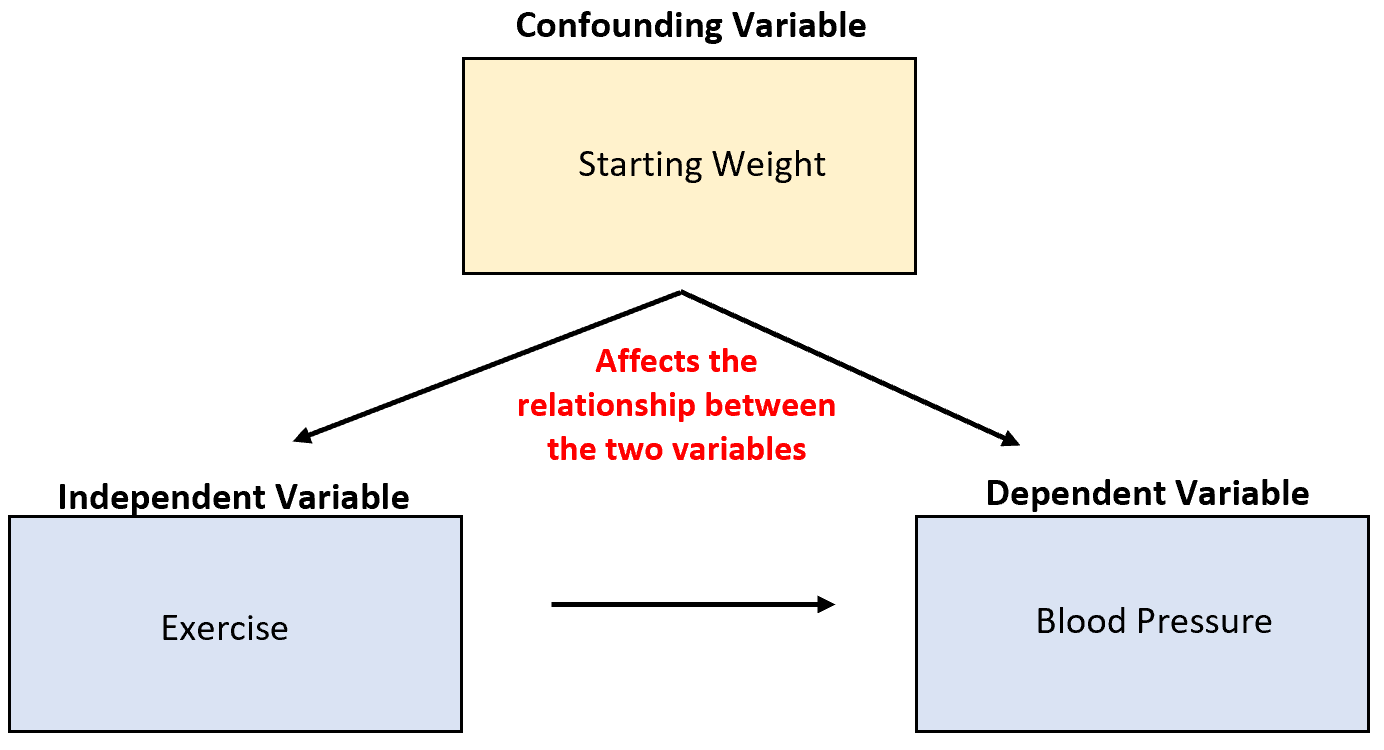
Ad esempio, supponiamo che un ricercatore raccolga dati sulle vendite di gelati e sugli attacchi di squali e scopra che le due variabili sono altamente correlate. Ciò significa che l’aumento delle vendite di gelati sta causando più attacchi di squali?

E ‘improbabile. La causa più probabile è la confusa temperatura variabile. Quando fuori fa più caldo, più persone acquistano il gelato e più persone vanno al mare.

Motivo 4: prendere decisioni migliori utilizzando le probabilità

Uno dei sottocampi più importanti della statistica è la probabilità . È il campo che studia la probabilità che si verifichino gli eventi.

Avendo una conoscenza di base della probabilità, puoi prendere decisioni più informate nel mondo reale.

Ad esempio, supponiamo che uno studente delle scuole superiori sappia di avere una probabilità del 10% di essere accettato in una determinata università. Utilizzando la formula per la probabilità di superare “almeno una” , questo studente può trovare la probabilità di essere accettato in almeno un’università alla quale si candida e può adeguare in base al risultato il numero di università a cui si candida.

Motivo 5: comprendere i valori P nella ricerca

Un altro concetto importante che imparerai nelle statistiche sono i valori p .

La definizione classica di valore p è:

Un valore p è la probabilità di osservare una statistica campionaria estrema almeno quanto la statistica campione, dato che l’ipotesi nulla è vera.

Ad esempio, supponiamo che una fabbrica affermi di produrre pneumatici con un peso medio di 200 libbre. Un revisore ipotizza che il peso medio effettivo degli pneumatici prodotti in questo stabilimento sia diverso di 200 libbre. Quindi esegue un test di ipotesi e scopre che il valore p del test è 0,04.

Ecco come interpretare questo valore p:

Se la fabbrica produce effettivamente pneumatici con un peso medio di 200 libbre, il 4% di tutti gli audit otterrà l’effetto osservato nel campione, o più, a causa di un errore di campionamento casuale. Questo ci dice che ottenere i dati campione ottenuti dal revisore sarebbe piuttosto raro se la fabbrica producesse effettivamente pneumatici con un peso medio di 200 libbre.

Pertanto, il revisore probabilmente rifiuterebbe l’ipotesi nulla secondo cui il peso medio effettivo degli pneumatici prodotti in questo stabilimento è effettivamente di 200 libbre.

Motivo 6: comprendere la correlazione

Un altro concetto importante che imparerai in statistica è la correlazione , che ci dice l’associazione lineare tra due variabili.

Il valore di un coefficiente di correlazione è sempre compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Comprendendo questi valori, puoi comprendere la relazione tra le variabili nel mondo reale.

Ad esempio, se la correlazione tra la spesa pubblicitaria e le entrate è 0,87, allora puoi capire che esiste una forte relazione positiva tra le due variabili. Man mano che spendi più soldi in pubblicità, puoi aspettarti un aumento prevedibile delle entrate.

Motivo 7: fare previsioni sul futuro

Un altro motivo importante per apprendere la statistica è comprendere modelli di regressione di base come:

• Regressione lineare semplice
• Regressione lineare multipla
• Regressione logistica

Ciascuno di questi modelli consente di effettuare previsioni sul valore futuro di una variabile di risposta in base al valore di determinate variabili predittive nel modello.

Ad esempio, le aziende utilizzano continuamente più modelli di regressione lineare nel mondo reale quando utilizzano variabili predittive come età, reddito, etnia, ecc. per prevedere quanti clienti spenderanno nei loro negozi.

Allo stesso modo, le società di logistica utilizzano variabili predittive come la domanda totale, la dimensione della popolazione, ecc. per prevedere le vendite future.

Indipendentemente dal campo in cui lavori, ci sono buone probabilità che i modelli di regressione vengano utilizzati per prevedere un fenomeno futuro.

Motivo 8: comprendere i potenziali bias negli studi

Un altro motivo per studiare la statistica è essere consapevoli di tutti i diversi tipi di pregiudizi che possono sorgere negli studi del mondo reale.

Ecco alcuni esempi:

• Osserva i pregiudizi
• Bias di autoselezione
• Distorsione di riferimento
• Distorsione da variabile omessa
• Sottovalutare i pregiudizi
• Distorsione da mancata risposta

Avendo una conoscenza di base di questi tipi di pregiudizi, puoi evitare di commetterli quando conduci ricerche o esserne consapevole quando leggi altri documenti o studi di ricerca.

Motivo 9: comprendere le ipotesi formulate dai test statistici

Molti test statistici fanno ipotesi sui dati sottostanti studiati.

Quando si leggono i risultati di uno studio o si conduce il proprio studio, è importante capire quali ipotesi è necessario fare affinché i risultati siano affidabili.

I seguenti articoli condividono le ipotesi formulate in molti test e procedure statistici comunemente utilizzati:

• Qual è l’ipotesi di equa varianza in statistica?
• Qual è il presupposto di normalità in statistica?
• Qual è il presupposto di indipendenza in statistica?

Motivo 10: evitare un’eccessiva generalizzazione

Un altro motivo per studiare la statistica è comprendere il concetto di ipergeneralizzazione .

Ciò si verifica quando gli individui che partecipano ad uno studio non sono rappresentativi degli individui della popolazione complessiva e pertanto non è appropriato generalizzare i risultati di uno studio all’intera popolazione.

Ad esempio, supponiamo di voler sapere quale percentuale di studenti di una determinata scuola preferisce il “dramma” come genere cinematografico preferito. Se la popolazione studentesca totale è un mix di 50% ragazzi e 50% ragazze, allora un campione composto da 90% ragazzi e 10% ragazze potrebbe portare a risultati distorti se un numero significativamente inferiore di ragazzi preferisce il teatro come genere preferito.

Idealmente, vogliamo che il nostro campione assomigli ad una “mini-versione” della nostra popolazione. Pertanto, se la popolazione studentesca complessiva fosse composta per il 50% da ragazze e per il 50% da ragazzi, il nostro campione non sarebbe rappresentativo se includesse il 90% di ragazzi e solo il 10% di ragazze.

Pertanto, sia che tu stia conducendo la tua indagine o leggendo i risultati di un sondaggio, è importante capire se i dati del campione sono rappresentativi della popolazione totale e se i risultati dell’indagine possono essere generalizzati con sicurezza alla popolazione.

Risorse addizionali

Consulta i seguenti articoli per acquisire una conoscenza di base dei concetti più importanti delle statistiche introduttive:

Statistica descrittiva o inferenziale
Popolazione vs. campione
Statistiche vs parametri
Variabili qualitative e quantitative
Livelli di misura: nominale, ordinale, intervallo e rapporto