Distribuzione di poisson o distribuzione normale: qual è la differenza?

La distribuzione di Poisson e la distribuzione normale sono due delle distribuzioni di probabilità più comunemente utilizzate in statistica.

Questo tutorial fornisce una rapida spiegazione di ciascuna distribuzione e due differenze chiave tra le distribuzioni.

Una panoramica: la distribuzione di Poisson

La distribuzione di Poisson descrive la probabilità di ottenere k successi durante un dato intervallo di tempo.

Se una variabile casuale X segue una distribuzione di Poisson, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = λ ^k * e ^{– λ} / k!

Oro:

• λ: numero medio di successi che si verificano durante un intervallo specifico
• k: numero di successi
• e: una costante pari a circa 2,71828

Ad esempio, supponiamo che in un particolare ospedale si verifichino in media 2 nascite all’ora. Possiamo usare la formula sopra per determinare la probabilità di avere 3 nascite in una determinata ora:

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

La probabilità di avere 3 nascite in una determinata ora è 0,1805 .

Una panoramica: la distribuzione normale

La distribuzione normale descrive la probabilità che una variabile casuale assuma un valore in un dato intervallo.

La funzione di densità di probabilità di una distribuzione normale può essere scritta come:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Oro:

• σ: deviazione standard della distribuzione
• μ: Media della distribuzione
• x: valore della variabile casuale

Ad esempio, supponiamo che il peso di una certa specie di lontre sia distribuito normalmente con μ = 40 libbre e σ = 5 libbre.

Se selezioniamo casualmente una lontra da questa popolazione, possiamo usare la seguente formula per trovare la probabilità che pesi tra 38 e 42 libbre:

P ( ^{38 < /5) 2} = 0,3108

La probabilità che la lontra selezionata casualmente pesi tra 38 e 42 libbre è 0,3108 .

Differenza n. 1: discreto vs. Dati continui

La prima differenza tra la distribuzione di Poisson e la distribuzione normale è il tipo di dati modellati da ciascuna distribuzione di probabilità.

Una distribuzione di Poisson viene utilizzata quando si lavora con dati discreti che possono assumere solo valori interi uguali o superiori a zero. Ecco alcuni esempi:

• Numero di chiamate ricevute all’ora in un call center
• Numero di clienti al giorno in un ristorante
• Numero di incidenti stradali al mese

In ogni scenario, la variabile casuale può assumere solo il valore 0, 1, 2, 3, ecc.

Una distribuzione normale viene utilizzata quando si lavora con dati continui che possono assumere qualsiasi valore dall’infinito negativo all’infinito positivo. Ecco alcuni esempi:

• Peso di un certo animale
• Altezza di una certa pianta
• Tempi della maratona femminile
• Temperatura in gradi Celsius

In questi scenari, le variabili casuali possono assumere qualsiasi valore come -11.3, 21.343435, 85, ecc.

Differenza n. 2: forma delle distribuzioni

La seconda differenza tra la distribuzione di Poisson e la distribuzione normale sta nella forma delle distribuzioni.

Una distribuzione normale avrà sempre una forma a campana:

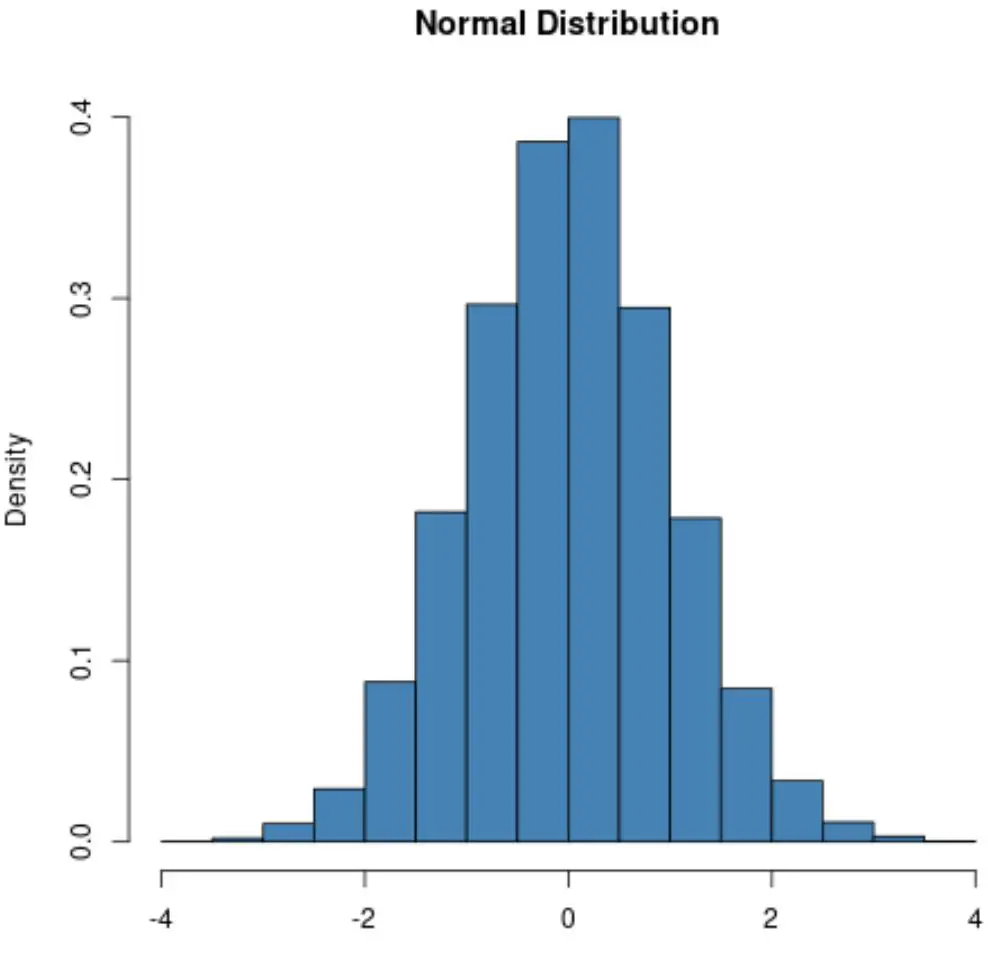
Tuttavia, la forma della distribuzione di Poisson varia a seconda del valore medio della distribuzione.

Ad esempio, una distribuzione di Poisson con un valore piccolo per la media come μ = 3 sarà fortemente distorta a destra :

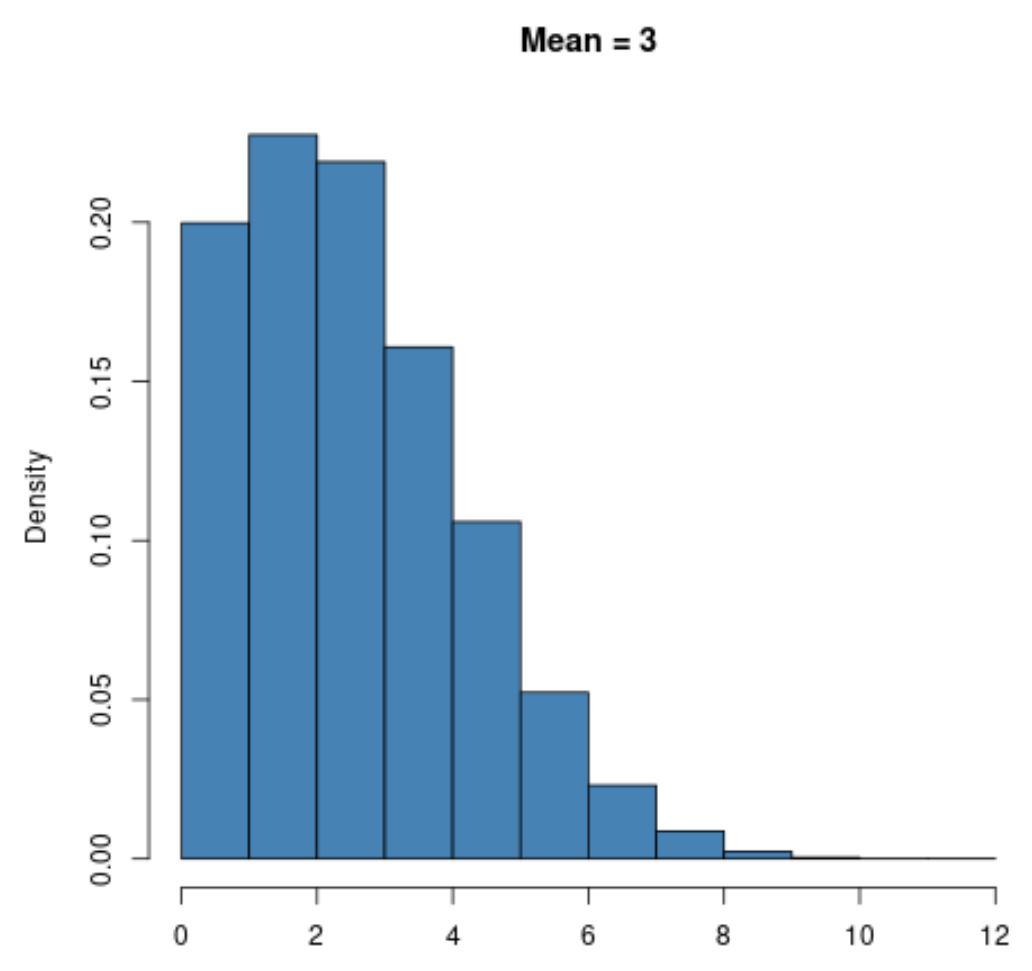
Tuttavia, una distribuzione di Poisson con un valore medio maggiore come μ = 20 presenterà una forma a campana proprio come la distribuzione normale:

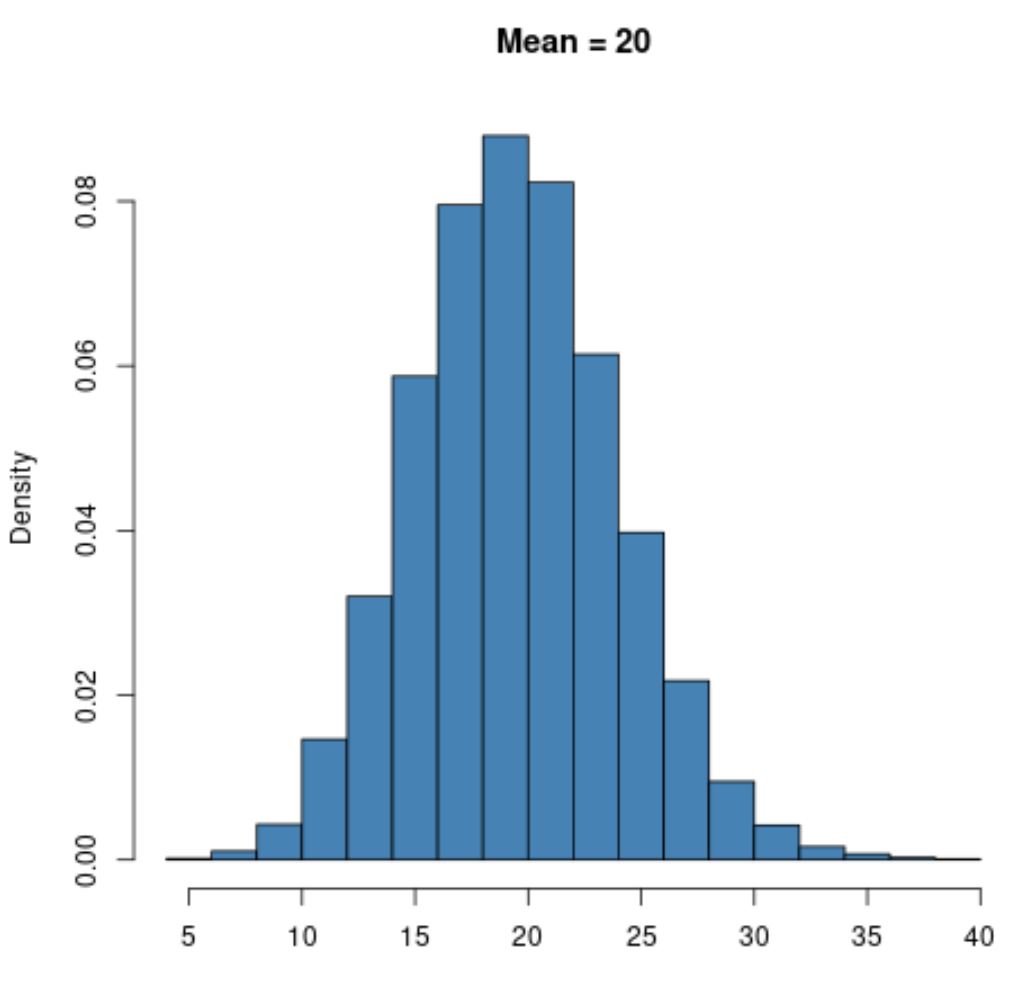
Si noti che il limite inferiore di una distribuzione di Poisson sarà sempre zero, indipendentemente dal valore della media, perché una distribuzione di Poisson può essere utilizzata solo con valori interi uguali o superiori a zero.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulla distribuzione di Poisson:

Un’introduzione alla distribuzione di Poisson
Le quattro ipotesi della distribuzione di Poisson
5 esempi concreti della distribuzione di Poisson

I seguenti tutorial forniscono informazioni aggiuntive sulla distribuzione normale:

Un’introduzione alla distribuzione normale
6 esempi concreti della distribuzione normale
Generatore di set di dati di distribuzione normale