Come utilizzare la distribuzione binomiale in python

La distribuzione binomiale è una delle distribuzioni più comunemente utilizzate in statistica. Descrive la probabilità di ottenere k successi in n esperimenti binomiali.

Se una variabile casuale X segue una distribuzione binomiale, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Oro:

• n: numero di prove
• k: numero di successi
• p: probabilità di successo in una determinata prova
• _n C _k : il numero di modi per ottenere k successi in n prove

Questo tutorial spiega come utilizzare la distribuzione binomiale in Python.

Come generare una distribuzione binomiale

Puoi generare un array di valori che segue una distribuzione binomiale utilizzando la funzione random.binomial della libreria Numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Ciascun numero nella tabella risultante rappresenta il numero di “successi” riscontrati nel corso di 10 prove in cui la probabilità di successo in una determinata prova era 0,25 .

Come calcolare le probabilità utilizzando una distribuzione binomiale

Puoi anche rispondere a domande sulla probabilità binomiale utilizzando la funzione binom della libreria Scipy.

Domanda 1: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui esattamente 10?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

La probabilità che Nathan effettui esattamente 10 tiri liberi è 0,0639 .

Domanda 2: Marty lancia una moneta equilibrata 5 volte. Qual è la probabilità che esca testa 2 volte o meno?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

La probabilità che la moneta esca testa 2 volte o meno è 0,5 .

Domanda 3: Sappiamo che il 70% delle persone sostiene una determinata legge. Se si scelgono a caso 10 individui, qual è la probabilità che tra 4 e 6 di loro sostengano la legge?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

La probabilità che tra 4 e 6 individui selezionati casualmente sostengano la legge è 0,3398 .

Come visualizzare una distribuzione binomiale

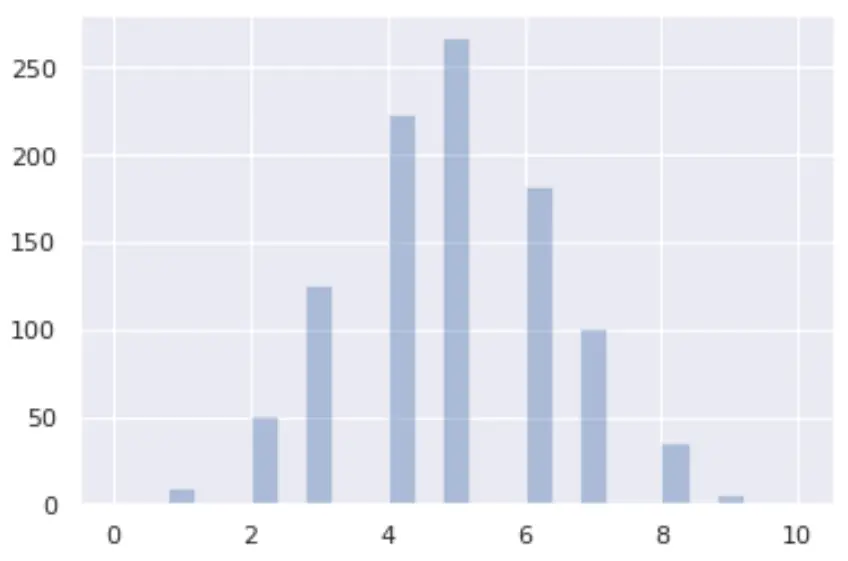
Puoi visualizzare una distribuzione binomiale in Python utilizzando le librerie seaborn e matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

Tè