Come utilizzare la distribuzione di poisson in python

La distribuzione di Poisson descrive la probabilità di ottenere k successi durante un dato intervallo di tempo.

Se una variabile casuale X segue una distribuzione di Poisson, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = λ ^k * e ^{– λ} / k!

Oro:

• λ: numero medio di successi che si verificano durante un intervallo specifico
• k: numero di successi
• e: una costante pari a circa 2,71828

Questo tutorial spiega come utilizzare la distribuzione di Poisson in Python.

Come generare una distribuzione di Poisson

Puoi utilizzare la funzione Poisson.rvs(mu, size) per generare valori casuali da una distribuzione di Poisson con un valore medio e una dimensione del campione specifici:

 from scipy. stats import fish

#generate random values from Poisson distribution with mean=3 and sample size=10
fish. rvs (mu=3, size=10)

array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])

Come calcolare le probabilità utilizzando una distribuzione di Poisson

È possibile utilizzare le funzioni Poisson.pmf(k, mu) e Poisson.cdf(k, mu) per calcolare le probabilità relative alla distribuzione di Poisson.

Esempio 1: Probabilità pari ad un certo valore

Un negozio vende in media 3 mele al giorno. Qual è la probabilità che vendano 5 mele in un dato giorno?

 from scipy. stats import fish

#calculate probability
fish. pmf (k=5, mu=3)

0.100819

La probabilità che il negozio venda 5 mele in un dato giorno è 0,100819 .

Esempio 2: Probabilità inferiore a un certo valore

Un certo negozio vende in media sette palloni da calcio al giorno. Qual è la probabilità che questo negozio venda quattro o meno palloni da calcio in un dato giorno?

 from scipy. stats import fish

#calculate probability
fish. cdf (k=4, mu=7)

0.172992

La probabilità che il negozio venda quattro o meno palloni da calcio in un dato giorno è 0,172992 .

Esempio 3: Probabilità maggiore di un certo valore

Un certo negozio vende in media 15 scatolette di tonno al giorno. Qual è la probabilità che questo negozio venda più di 20 scatolette di tonno in un dato giorno?

 from scipy. stats import fish

#calculate probability
1-fish. cdf (k=20, mu=15)

0.082971

La probabilità che il negozio venda più di 20 scatolette di tonno in un dato giorno è 0,082971 .

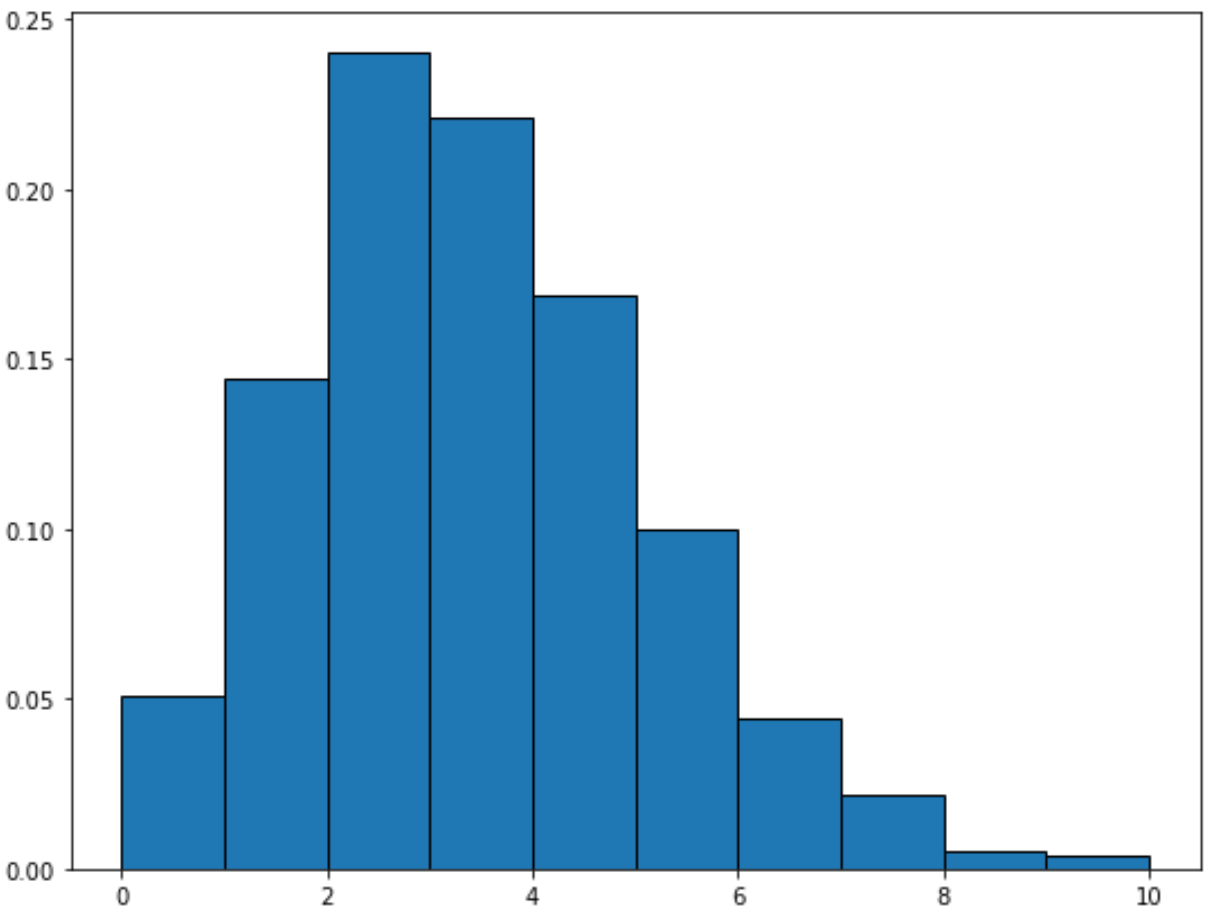
Come tracciare una distribuzione di Poisson

È possibile utilizzare la seguente sintassi per tracciare una distribuzione di Poisson con una determinata media:

 from scipy. stats import fish
import matplotlib. pyplot as plt

#generate Poisson distribution with sample size 10000
x = fish. rvs (mu=3, size=10000)

#create plot of Poisson distribution
plt. hist (x, density= True , edgecolor=' black ')

Risorse addizionali

Un’introduzione alla distribuzione di Poisson
5 esempi concreti della distribuzione di Poisson
Calcolatore online della distribuzione del pesce