Come eseguire la regressione cubica in python

La regressione cubica è un tipo di regressione che possiamo utilizzare per quantificare la relazione tra una variabile predittrice e una variabile di risposta quando la relazione tra le variabili non è lineare.

Questo tutorial spiega come eseguire la regressione cubica in Python.

Esempio: regressione cubica in Python

Supponiamo di avere il seguente DataFrame panda che contiene due variabili (xey):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Se creiamo un semplice grafico a dispersione di questi dati, possiamo vedere che la relazione tra le due variabili non è lineare:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

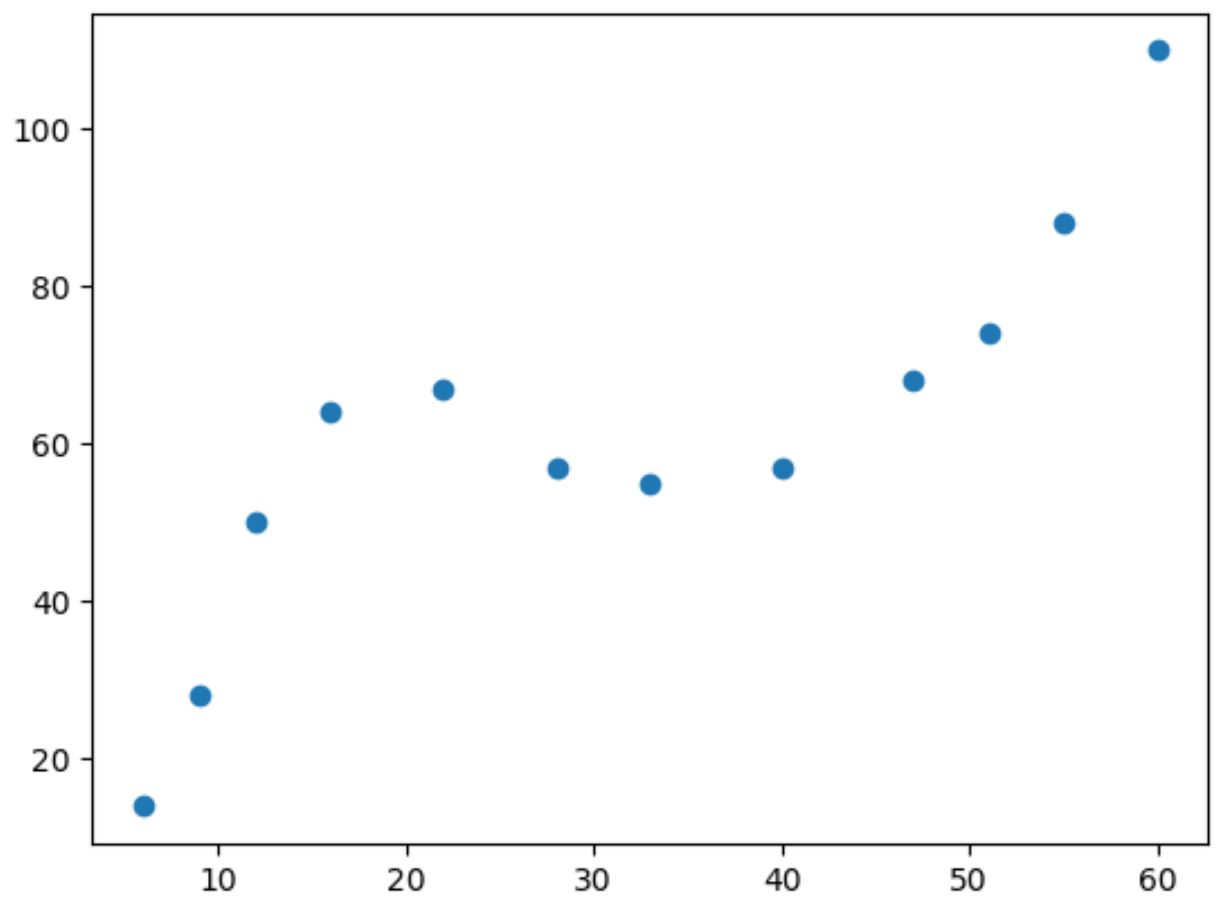
All’aumentare del valore di x, y aumenta fino a un certo punto, poi diminuisce, quindi aumenta di nuovo.

Questo modello con due “curve” nel grafico indica una relazione cubica tra le due variabili.

Ciò significa che un modello di regressione cubica è un buon candidato per quantificare la relazione tra le due variabili.

Per eseguire la regressione cubica, possiamo adattare un modello di regressione polinomiale di grado 3 utilizzando la funzione numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

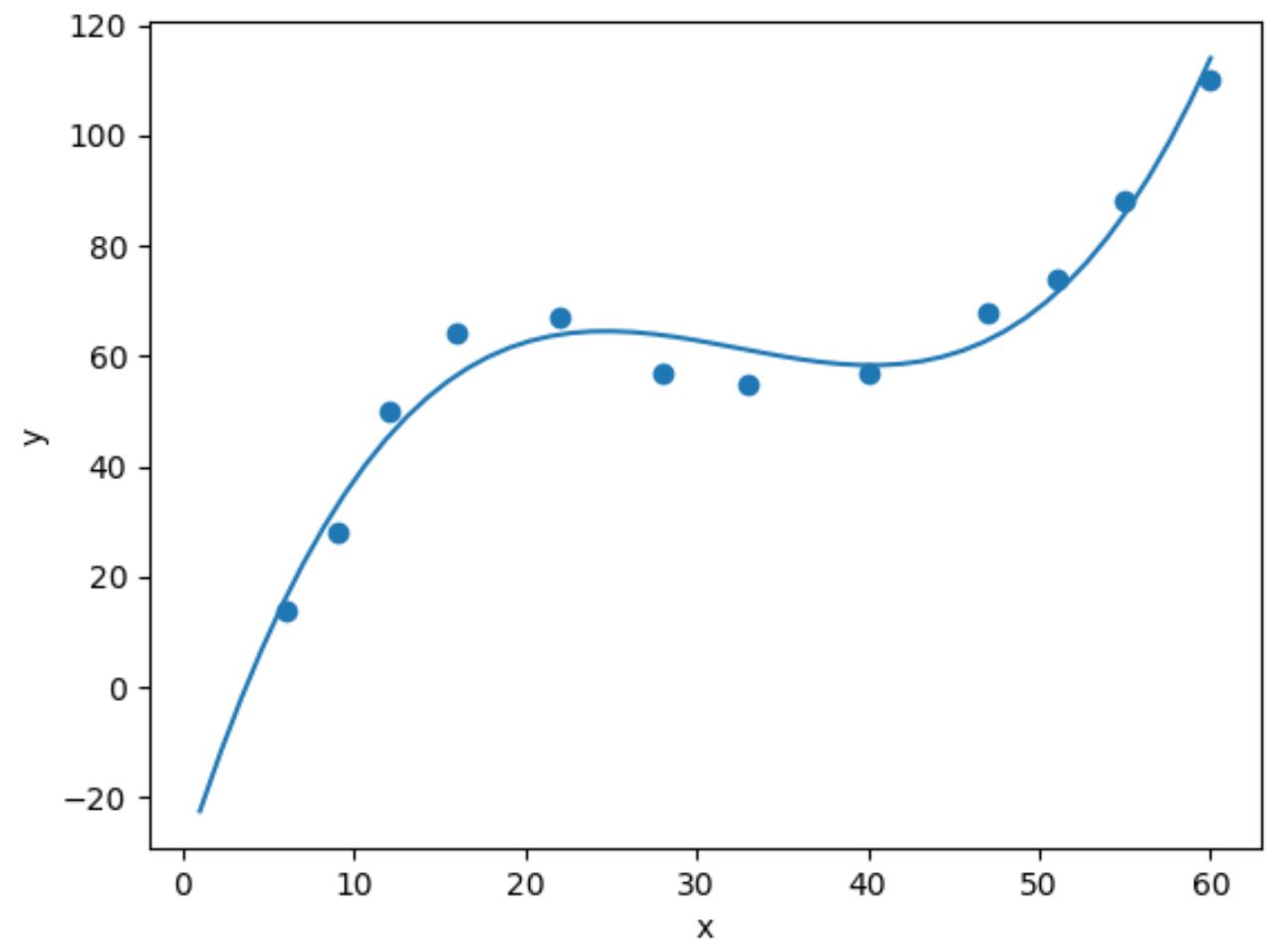
Possiamo ottenere l’equazione di regressione cubica adattata stampando i coefficienti del modello:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

L’equazione di regressione cubica adattata è:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Possiamo usare questa equazione per calcolare il valore atteso di y in base al valore di x.

Ad esempio, se x è 30, il valore previsto per y è 64,844:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Possiamo anche scrivere una breve funzione per ottenere l’R quadrato del modello, ovvero la proporzione della varianza nella variabile di risposta che può essere spiegata dalle variabili predittive.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

In questo esempio, il quadrato R del modello è 0,9632 .

Ciò significa che il 96,32% della variazione nella variabile di risposta può essere spiegato dalla variabile predittore.

Poiché questo valore è così alto, ci dice che il modello di regressione cubica quantifica bene la relazione tra le due variabili.

Correlato: Qual è un buon valore R quadrato?

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Python:

Come eseguire una semplice regressione lineare in Python
Come eseguire la regressione quadratica in Python
Come eseguire la regressione polinomiale in Python