Come eseguire una trasformazione box-cox in python

Una trasformazione box-cox è un metodo comunemente utilizzato per trasformare un set di dati non distribuito normalmente in un set distribuito più normalmente .

L’idea alla base di questo metodo è trovare un valore per λ tale che i dati trasformati siano il più vicino possibile alla distribuzione normale, utilizzando la seguente formula:

• y(λ) = (y ^λ – 1) / λ se y ≠ 0
• y(λ) = log(y) se y = 0

Possiamo eseguire una trasformazione box-cox in Python utilizzando la funzione scipy.stats.boxcox() .

L’esempio seguente mostra come utilizzare questa funzione nella pratica.

Esempio: trasformazione di Box-Cox in Python

Supponiamo di generare un insieme casuale di 1000 valori da una distribuzione esponenziale :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

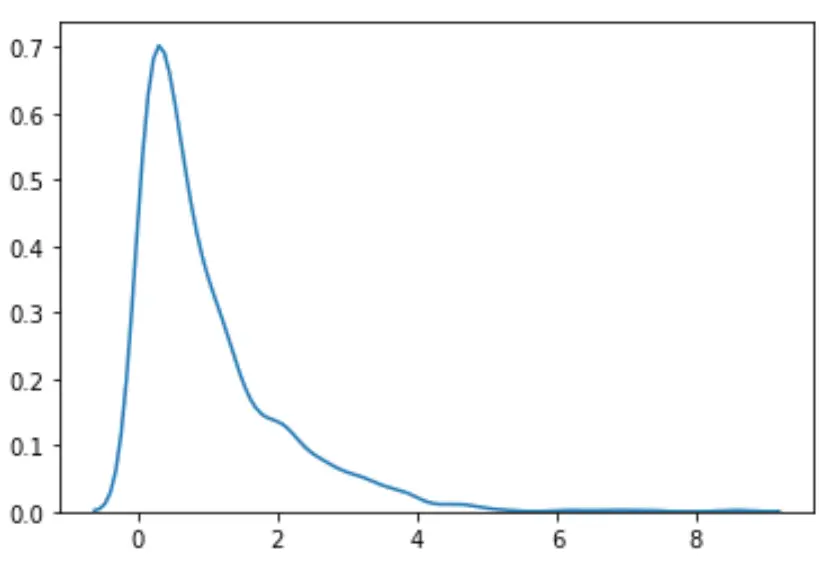
Possiamo vedere che la distribuzione non sembra normale.

Possiamo usare la funzione boxcox() per trovare un valore ottimale di lambda che produca una distribuzione più normale:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

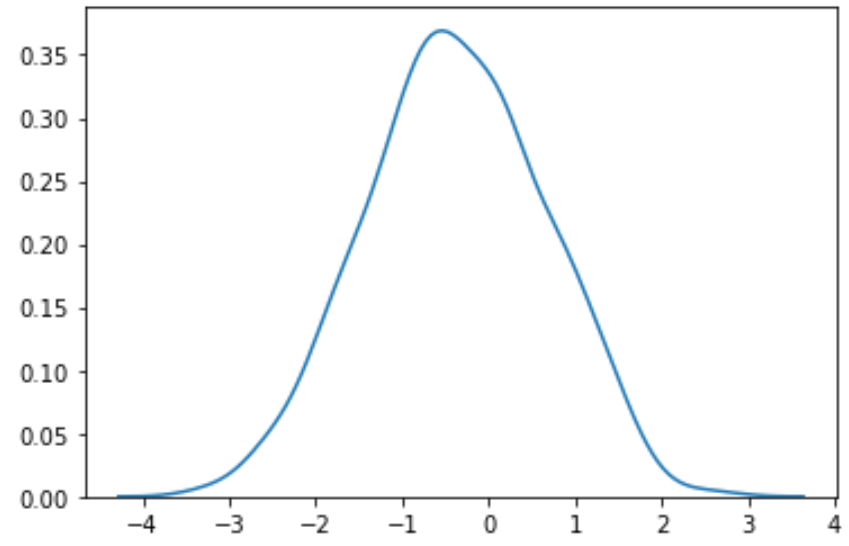
Possiamo vedere che i dati trasformati seguono una distribuzione molto più normale.

Possiamo anche trovare l’esatto valore lambda utilizzato per eseguire la trasformazione di Box-Cox:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

Il lambda ottimale è risultato essere intorno a 0,242 .

Pertanto, ciascun valore dei dati è stato trasformato utilizzando la seguente equazione:

Nuovo = (vecchio ^0,242 – 1) / 0,242

Possiamo confermarlo osservando i valori dei dati originali rispetto ai dati trasformati:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

Il primo valore nel set di dati originale era 0.79587 . Quindi, abbiamo applicato la seguente formula per trasformare questo valore:

Nuovo = (0,79587 ^0,242 – 1) / 0,242 = -0,222

Possiamo confermare che il primo valore nel set di dati trasformato è effettivamente -0.222 .

Risorse addizionali

Come creare e interpretare un grafico QQ in Python
Come eseguire un test di normalità di Shapiro-Wilk in Python