Bias di berkson: definizione + esempi

Il bias di Berkson è un tipo di bias che si verifica nella ricerca quando due variabili sembrano essere correlate negativamente nei dati di un campione, ma in realtà sono correlate positivamente nella popolazione complessiva.

Ad esempio, supponiamo che Tom voglia studiare la correlazione tra la qualità degli hamburger e dei frappè nei ristoranti locali.

Esce e raccoglie i seguenti dati su sette diversi ristoranti:

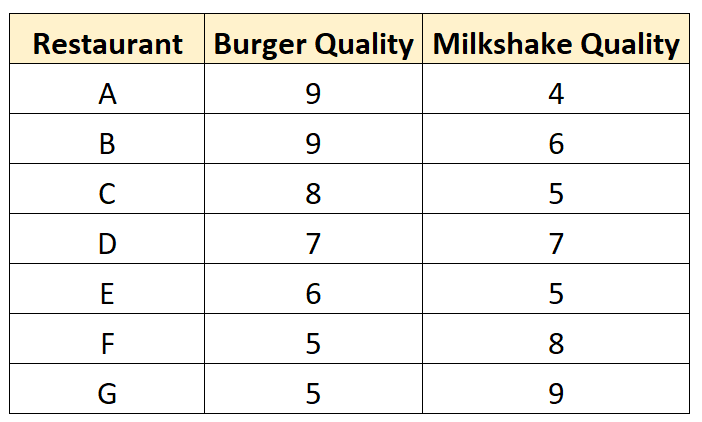
Crea un grafico a dispersione per visualizzare i dati:

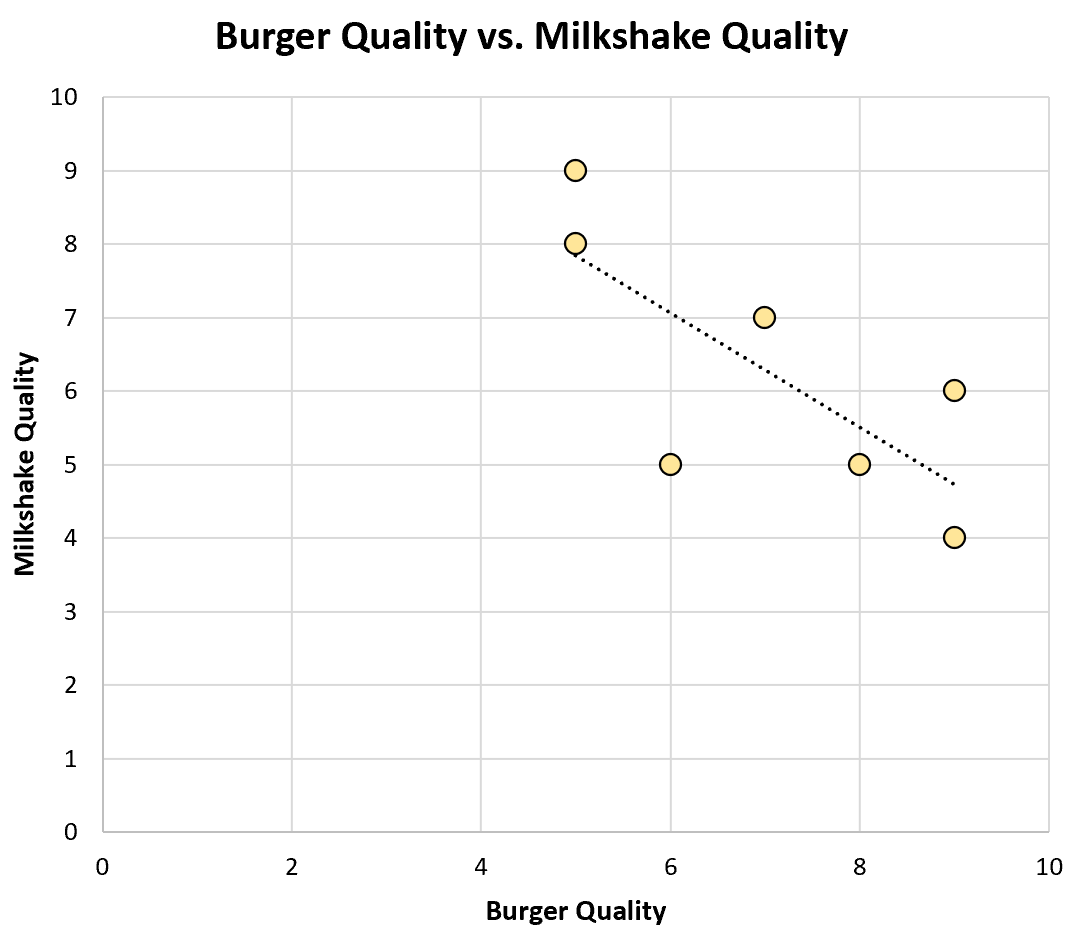
Il coefficiente di correlazione di Pearson tra queste due variabili è -0,75 , che corrisponde a una forte correlazione negativa.

Questa scoperta è controintuitiva per Tom: penserebbe che i ristoranti che fanno buoni hamburger facciano anche buoni frappè.

Tuttavia, si scopre che Tom ha semplicemente ignorato tutti i ristoranti della città che producono sia hamburger scadenti che frappè scadenti.

Se avesse visitato questi ristoranti, avrebbe raccolto il seguente set di dati:

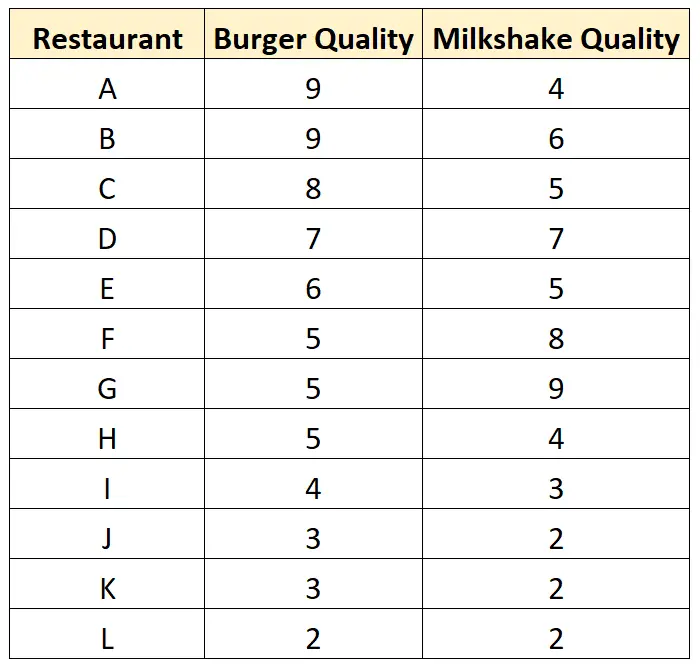
Ed ecco come appare un grafico a dispersione per questo set di dati:

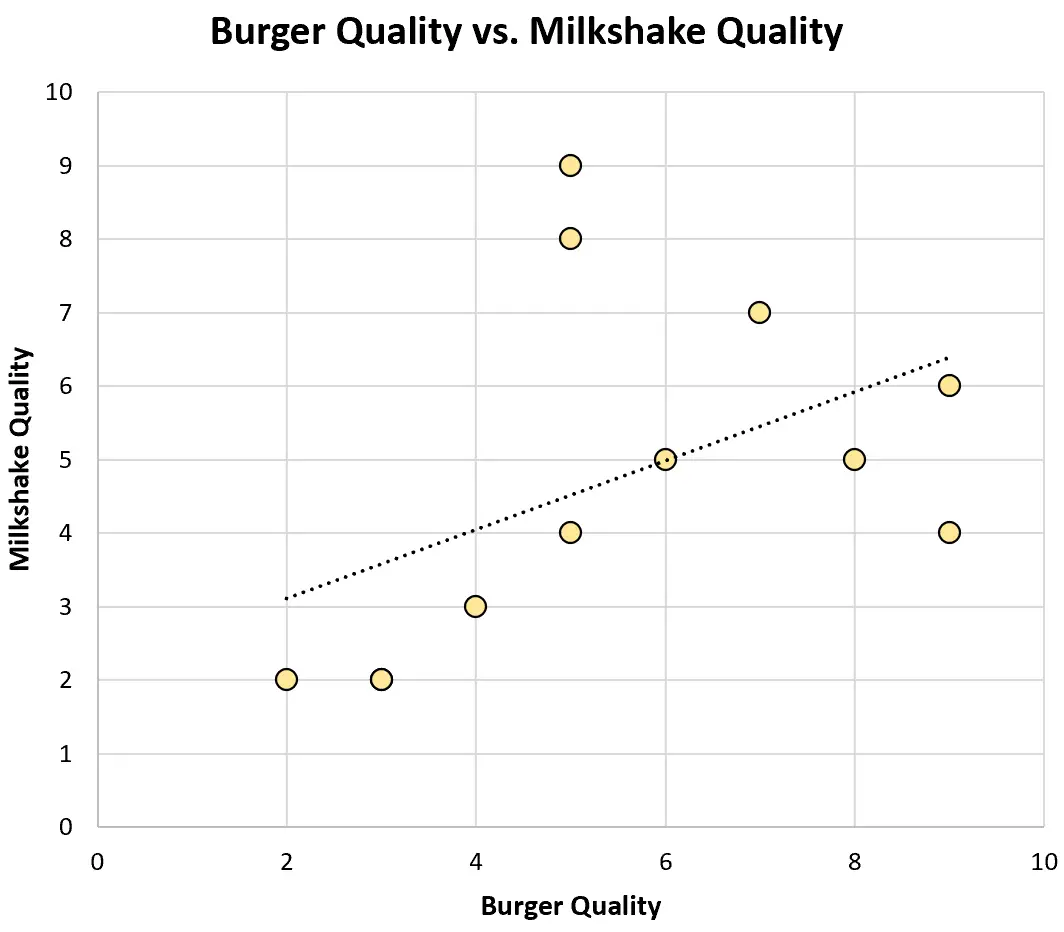
Il coefficiente di correlazione di Pearson tra le due variabili risulta essere 0,46 , che rappresenta una correlazione positiva moderatamente forte.

Esaminando solo un sottoinsieme dei ristoranti della città, Tom ha erroneamente concluso che esisteva una correlazione negativa tra la qualità degli hamburger e dei frappè.

In effetti, risulta che esiste una relazione positiva (come ci si aspetterebbe) tra queste due variabili. Questo è un classico esempio del pregiudizio di Berkson.

Vedere gli esempi seguenti per altri scenari in cui nella pratica si verifica il bias di Berkson.

Esempio 1: Ammissioni al college

Supponiamo che un college ammetta solo gli studenti che hanno un punteggio GPA e ACT sufficientemente alto.

È noto che queste due variabili sono correlate positivamente, ma risulta che tra gli studenti che decidono di frequentare un determinato college sembra esserci una correlazione negativa tra le due.

Tuttavia, questa correlazione negativa si verifica solo perché gli studenti che hanno sia un punteggio GPA che ACT elevato sono in grado di frequentare un’università d’élite, mentre gli studenti che hanno sia un punteggio GPA che ACT basso non sono ammessi affatto.

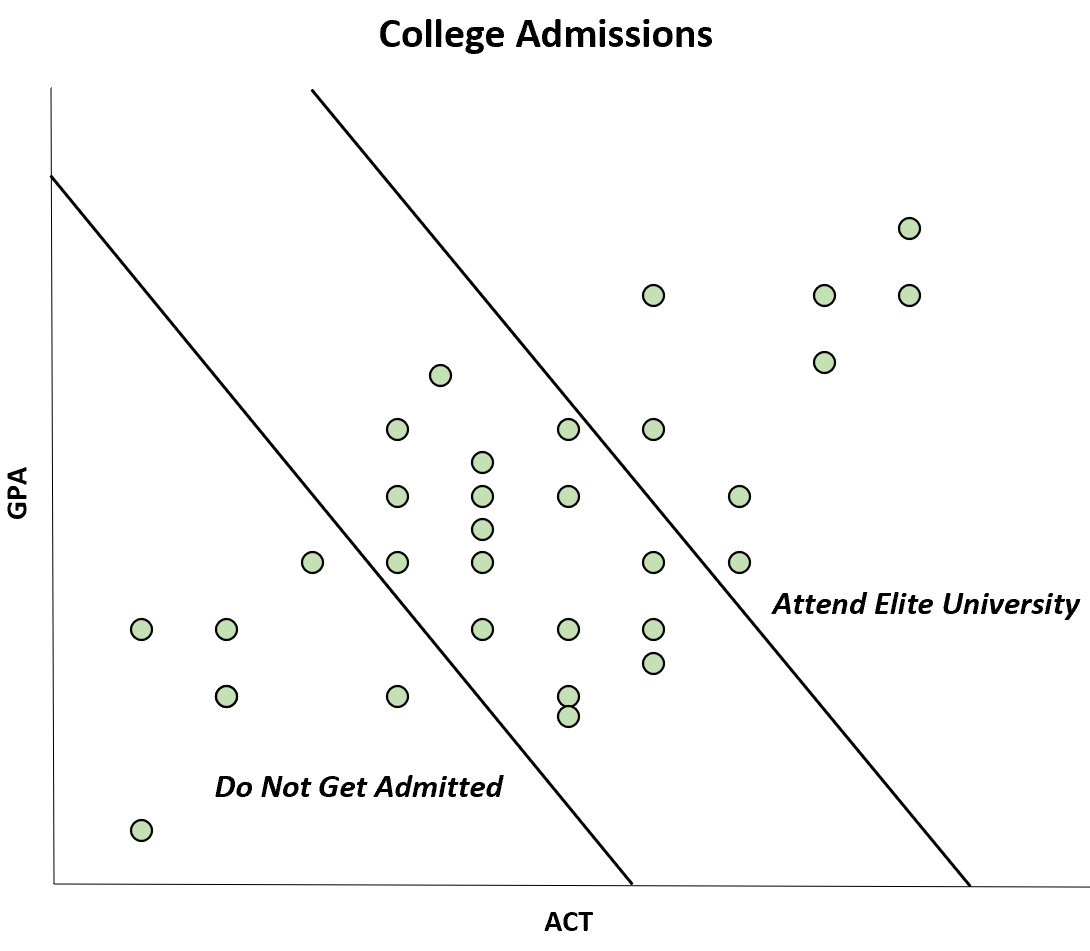
Sebbene la correlazione tra ACT e GPA sia positiva nella popolazione, la correlazione appare negativa nel campione. Questo è un caso di parzialità da parte di Berkson.

Esempio 2: Preferenze di appuntamenti

Molte persone escono solo con partner che siano attraenti e abbiano una buona personalità.

Nel mondo reale, potrebbe non esserci alcuna correlazione tra queste due variabili, ma quando si restringe il pool di appuntamenti, un individuo può ignorare completamente i potenziali partner che sono allo stesso tempo poco attraenti e dotati. ‘una buona personalità.

Quindi, tra i potenziali partner, può sembrare che esista una correlazione negativa tra queste due variabili: le persone più attraenti hanno personalità peggiori, e le persone con personalità migliori sembrano meno attraenti.

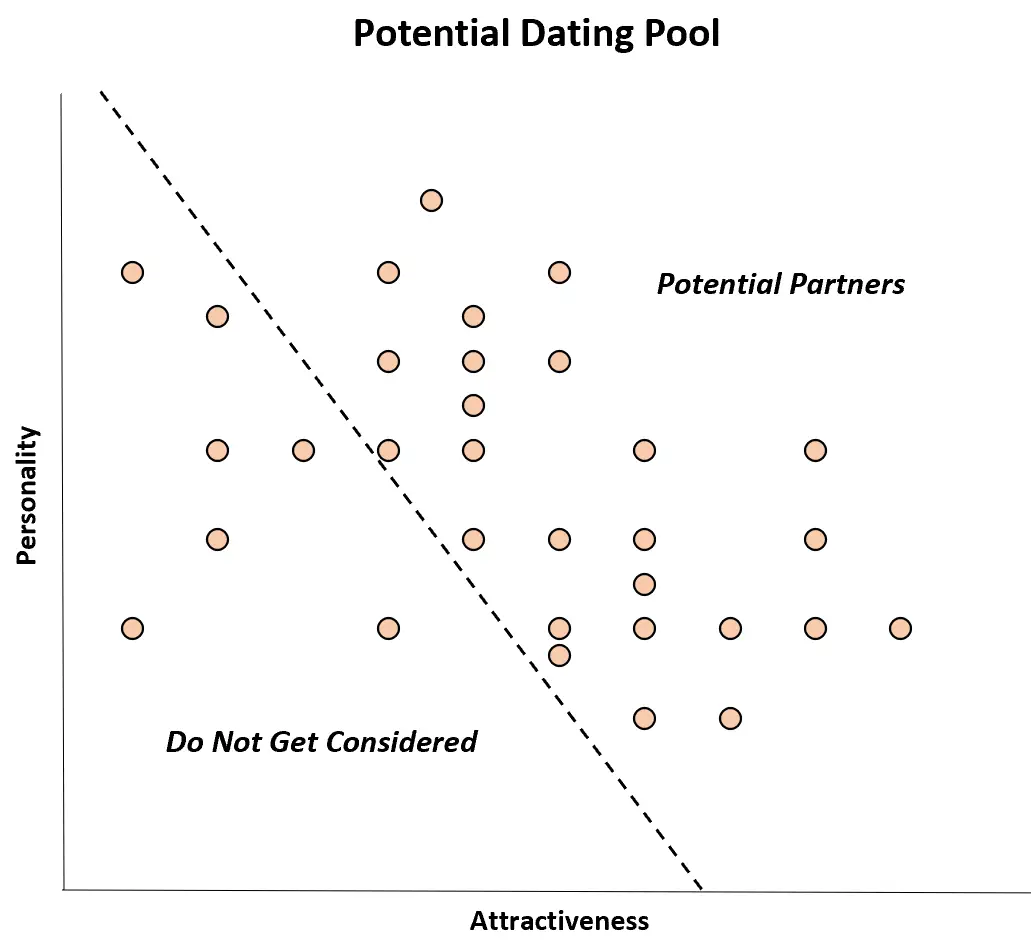
Sebbene non vi sia alcuna correlazione tra queste due variabili nella popolazione, sembra esserci una correlazione negativa nel campione dei potenziali partner. Questo è semplicemente un caso di pregiudizio di Berkson.

Come prevenire i pregiudizi di Berkson

Il modo più ovvio per evitare la distorsione di Berkson negli studi di ricerca è raccogliere un semplice campione casuale da una popolazione. In altre parole, assicurarsi che ciascun membro della popolazione di interesse abbia le stesse possibilità di essere incluso nel campione.

Ad esempio, se stai studiando la prevalenza della malattia in un determinato paese, devi raccogliere un campione di individui provenienti da tutto il paese, non solo quelli facilmente raggiungibili negli ospedali.

Utilizzando un campione casuale semplice, i ricercatori possono massimizzare la possibilità che il loro campione sia rappresentativo della popolazione, il che significa che possono generalizzare con sicurezza i loro risultati dal campione alla popolazione complessiva.