Probabilità posteriore: definizione + esempio

La probabilità a posteriori è la probabilità aggiornata che un evento si verifichi dopo aver preso in considerazione nuove informazioni.

Ad esempio, potremmo essere interessati alla probabilità che si verifichi un evento “A” dopo aver contabilizzato un evento “B” appena accaduto. Potremmo calcolare questa probabilità a posteriori utilizzando la seguente formula:

P(A|B) = P(A) * P(B|A) / P(B)

Oro:

P(A|B) = la probabilità che si verifichi l’evento A, dato che si è verificato l’evento B. Si noti che “| » significa “dato”.

P(A) = la probabilità che si verifichi l’evento A.

P(B) = la probabilità che si verifichi l’evento B.

P(B|A) = la probabilità che si verifichi l’evento B, dato che si è verificato l’evento A.

Esempio: calcolo della probabilità a posteriori

Un bosco è composto per il 20% da querce e per l’80% da aceri. Supponiamo di sapere che il 90% delle querce è sano mentre solo il 50% degli aceri è sano. Supponiamo che da lontano si possa dire che un particolare albero è sano. Qual è la probabilità che l’albero sia una quercia?

Ricordiamo che la probabilità che si verifichi l’evento A dato che si è verificato l’evento B è:

P(A|B) = P(A) * P(B|A) / P(B)

In questo esempio, la probabilità che l’albero sia una quercia dato che l’albero è sano è:

P(Quercia|Quercia sana) = P(Quercia) * P(Quercia sana|Quercia) / P(Quercia sana)

P(Quercia) = La probabilità che un dato albero sia una quercia è 0,2 perché il 20% di tutti gli alberi della foresta sono querce.

P(Sano) = La probabilità che un dato albero sia sano può essere calcolata come segue: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Sano|Quercia) = La probabilità che un albero sia sano dato che è una quercia è 0,9 , poiché ci è stato detto che il 90% delle querce sono sane.

Utilizzando questi tre numeri possiamo trovare la probabilità che l’albero sia una quercia dato che è sano:

P(Rovere|Sano) = P(Rovere) * P(Sano|Rovere) / P(Sano) = (0,2) * (0,9) / (0,58) = 0,3103 .

Per una comprensione intuitiva di questa probabilità, supponiamo che la griglia seguente rappresenti questa foresta di 100 alberi. Esattamente 20 alberi sono querce e 18 sono sani. Gli altri 80 alberi sono aceri e di questi 40 sono sani.

(O = quercia, M = acero, verde = sano, rosso = malsano)

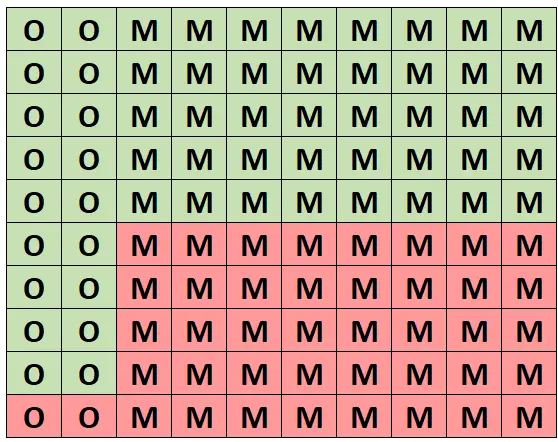
Di tutti gli alberi, esattamente 58 sono sani e 18 di questi alberi sani sono querce. Quindi, se sappiamo di aver selezionato un albero sano allora la probabilità che si tratti di una quercia è 18/58 = 0,3103 .

Quando dovresti usare la probabilità a posteriori?

La probabilità a posteriori viene utilizzata in un’ampia varietà di campi, tra cui finanza, medicina, economia e previsioni meteorologiche.

Lo scopo dell’utilizzo delle probabilità a posteriori è aggiornare una convinzione precedente che avevamo su qualcosa una volta ottenute nuove informazioni.

Ricordiamo dall’esempio precedente che sapevamo che la probabilità che un dato albero nella foresta fosse quercia era del 20%. Questa è chiamata probabilità a priori . Se scegliessimo semplicemente un albero a caso, sapremmo che la probabilità che sia una quercia era 0,20.

Tuttavia, una volta ottenute le nuove informazioni secondo cui l’albero da noi selezionato era sano, siamo stati in grado di utilizzare queste nuove informazioni per determinare che la probabilità a posteriori che questo albero fosse una quercia era invece 0,3103.

Nel mondo reale, le persone scoprono costantemente nuove informazioni. Queste nuove informazioni ci aiutano ad aggiornare le nostre convinzioni precedenti. In termini statistici, ciò significa che siamo in grado di generare probabilità a posteriori degli eventi che si verificano, il che ci aiuta ad acquisire una comprensione più accurata del mondo e ci consente di fare previsioni più accurate sugli eventi futuri.