Il problema di monty hall: una semplice spiegazione visiva

In un vecchio game show chiamato Let’s Make a Deal , il conduttore Monty Hall presentava ai concorrenti tre porte.

Una delle porte conteneva un premio mentre le altre due no.

Monty chiedeva al concorrente di scegliere quale porta pensava contenesse il premio.

Una volta che il concorrente aveva selezionato una porta, Monty apriva una porta che non conteneva il premio.

Il premio è rimasto in una delle due porte chiuse.

Monty avrebbe quindi chiesto al candidato se voleva cambiare porta.

Anche se può sembrare difficile da credere, si scopre che cambiare porta a questo punto del gioco ti dà effettivamente maggiori possibilità di vincere.

Continua a leggere per scoprire perché!

Il problema di Monty Hall spiegato visivamente

Per illustrare perché cambiare porta ti dà una maggiore probabilità di vincita, considera i seguenti scenari in cui scegli prima la porta 1.

Scenario 1: scegli la porta 1 e il premio è effettivamente dietro la porta 1.

In questo caso, Monty aprirà la porta 2 o 3 e ti mostrerà che non c’è niente dietro nessuna delle due porte. Se rimani con la porta 1, vinci .

Scenario 2: scegli la porta 1 e il premio è effettivamente dietro la porta 2.

In questo caso Monty dovrà aprire la porta 3 e mostrarvi che dietro non c’è nulla. Se rimani con la porta 1, perdi .

Scenario 3: scegli la porta 1 e il premio è effettivamente dietro la porta 3.

In questo caso Monty deve aprire la porta 2 e mostrarti che dietro non c’è nulla. Se rimani con la porta 1, perdi .

Questi sono tutti i risultati possibili se scegli la porta 1. Tieni presente che se rimani con la porta 1, risparmierai solo un terzo del tempo. Ma se cambi, risparmi due terzi del tempo.

La tabella seguente riassume tutti i possibili scenari in questo game show, nonché i risultati associati al mantenimento e alla modifica:

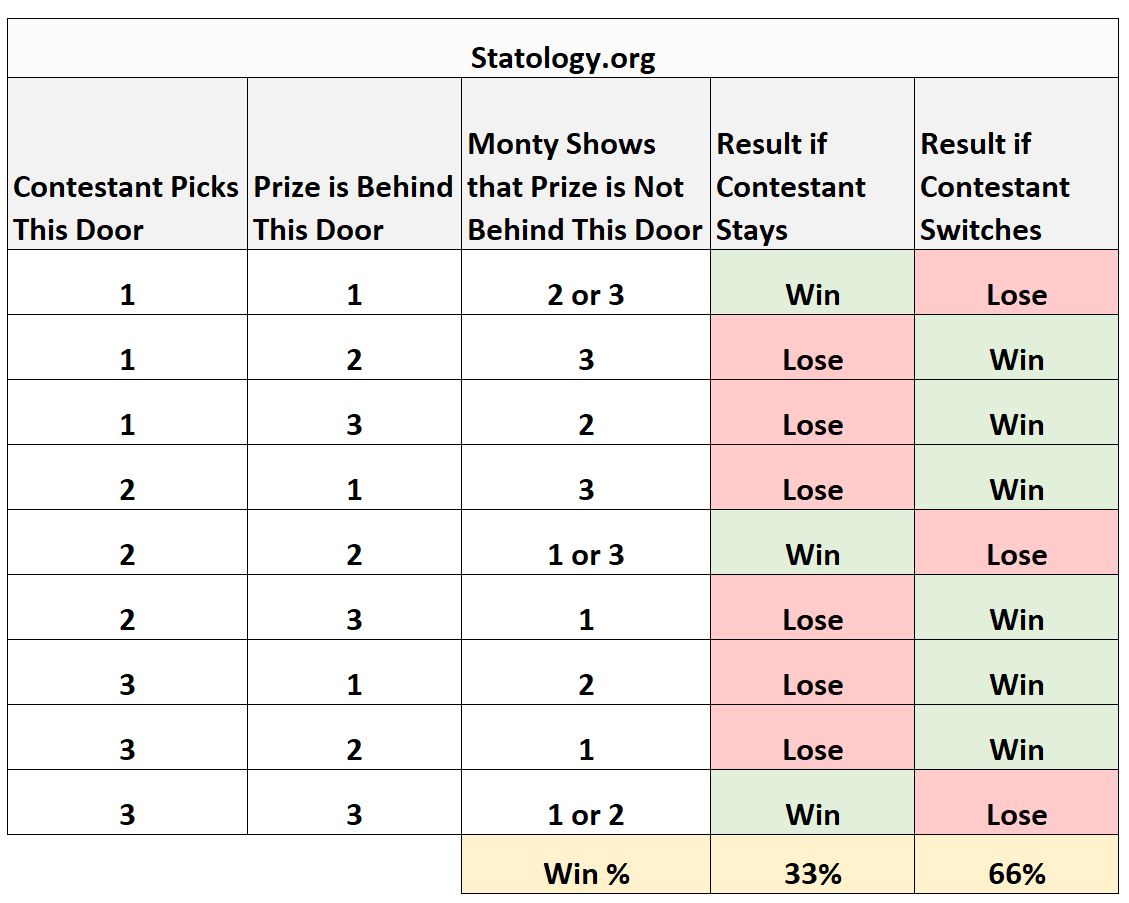
Dalla tabella, possiamo vedere che vinci il 33% delle volte quando rimani, ma vinci il 66% delle volte quando cambi.

Quindi, cambiare porta aumenta la probabilità di vincere il premio.

Anche se intuitivamente questo potrebbe non avere senso, i conti non mentono.