Una guida alla procedura benjamini-hochberg

Ogni volta che esegui un test statistico, è possibile che otterrai un valore p inferiore a 0,05 per puro caso, anche se la tua ipotesi nulla è vera.

Ad esempio, supponiamo che tu voglia sapere se una determinata pianta ha un’altezza media superiore a 10 pollici. Le tue ipotesi nulle e alternative per il test sarebbero:

_H0 : μ = 10 pollici

H _A : μ > 10 pollici

Per verificare questa ipotesi, puoi uscire e raccogliere un campione casuale di 20 piante da misurare. Anche se la vera altezza media di questa specie di pianta è di 10 pollici, è possibile che tu abbia selezionato un campione di 20 piante insolitamente alte, portandoti a rifiutare l’ipotesi nulla.

Anche se l’ipotesi nulla fosse vera (l’altezza media di questa pianta era in realtà di 10 pollici), l’hai rifiutata. Nelle statistiche, ciò lo chiamiamo “falsa scoperta”. Lei sostiene di aver fatto una scoperta – un “risultato significativo” – ma in realtà è falso.

Ora immagina di eseguire 100 test statistici contemporaneamente. Utilizzando un livello alfa di 0,05, c’è solo il 5% di possibilità di fare una falsa scoperta con un singolo test, ma poiché stai eseguendo un numero così elevato di test, ti aspetteresti che solo circa 5 su 100 portino a false scoperte.

Nel mondo moderno, le false scoperte possono essere un problema comune poiché la tecnologia ha consentito ai ricercatori di eseguire centinaia o addirittura migliaia di test statistici alla volta.

Ad esempio, i ricercatori medici possono eseguire test statistici su decine di migliaia di geni alla volta. Anche con un tasso di false scoperte di appena il 5%, ciò significa che centinaia di test potrebbero portare a false scoperte.

Un modo per controllare il tasso di false scoperte è utilizzare la cosiddetta procedura Benjamini-Hochberg.

Il procedimento Benjamini-Hochberg

La procedura Benjamini-Hochberg funziona come segue:

Passaggio 1: esegui tutti i test statistici e trova il valore p per ciascun test.

Passaggio 2: classifica i valori p in ordine decrescente, assegnando a ciascuno un rango: il valore più piccolo ha un rango 1, il successivo più piccolo ha un rango 2, ecc.

Passaggio 3: calcolare il valore critico Benjamini-Hochberg per ciascun valore p, utilizzando la formula (i/m)*Q

Oro:

i = rango del valore p

m = numero totale di test

Q = tasso di false scoperte scelto

Passaggio 4: trovare il valore p più grande inferiore al valore critico. Designare ogni valore p inferiore a questo valore p come significativo.

L’esempio seguente illustra come eseguire questa procedura con valori concreti.

Esempio

Diciamo che i ricercatori vogliono determinare se 20 diverse variabili sono correlate o meno alle malattie cardiache. Eseguono 20 test statistici individuali alla volta e ricevono un valore p per ciascun test. La tabella seguente mostra i valori p per ciascun test, elencati in ordine decrescente.

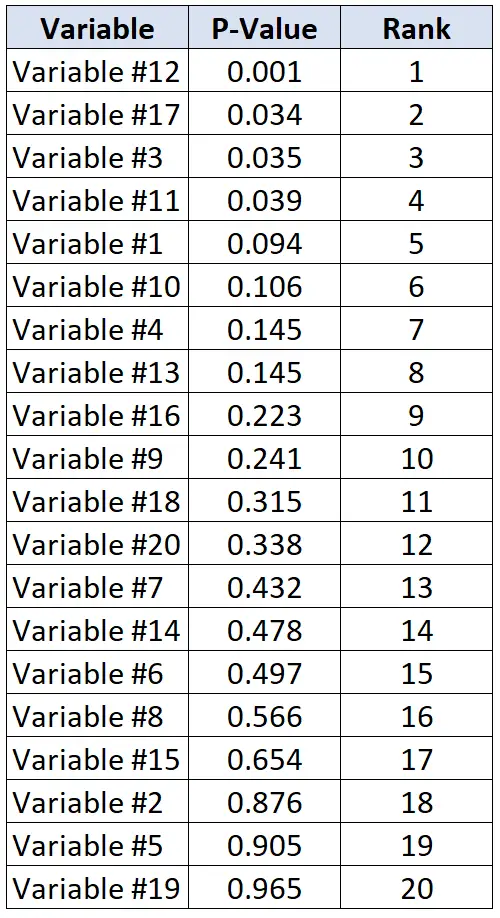
Supponiamo che i ricercatori siano disposti ad accettare un tasso di false scoperte del 20%. Quindi, per calcolare il valore critico Benjamini-Hochberg per ciascun valore p, possiamo utilizzare la seguente formula: (i/20)*0.2 dove i = rango del valore p.

La tabella seguente mostra il valore critico Benjamini-Hochberg per ogni singolo valore p:

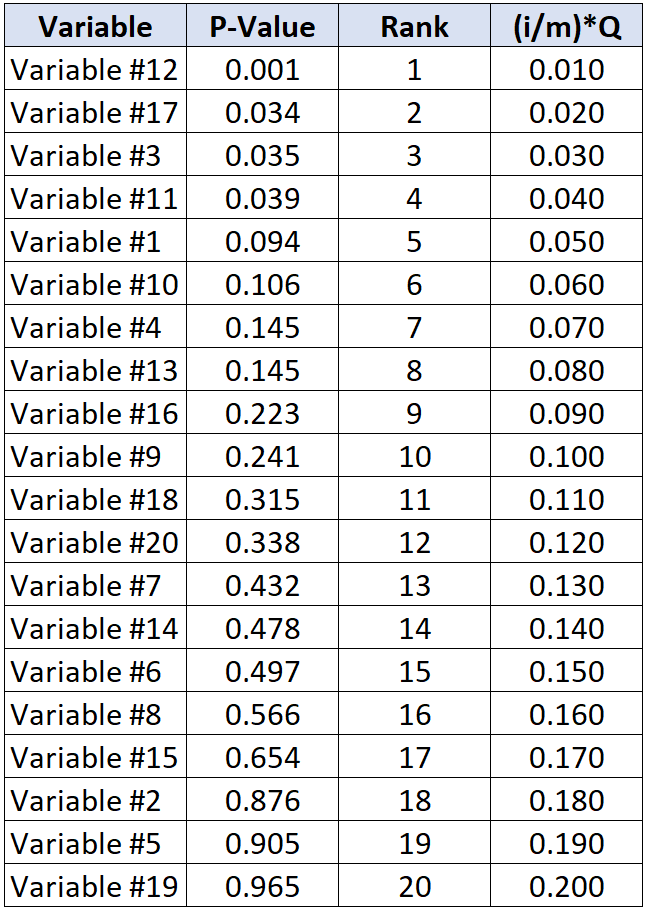
Il test con il valore p più grande al di sotto del valore critico Benjamini-Hochberg è la variabile n. 11, che ha un valore p di 0,039 e un valore critico BH di 0,040.

Pertanto, questo test e tutti i test con un valore p inferiore saranno considerati significativi.

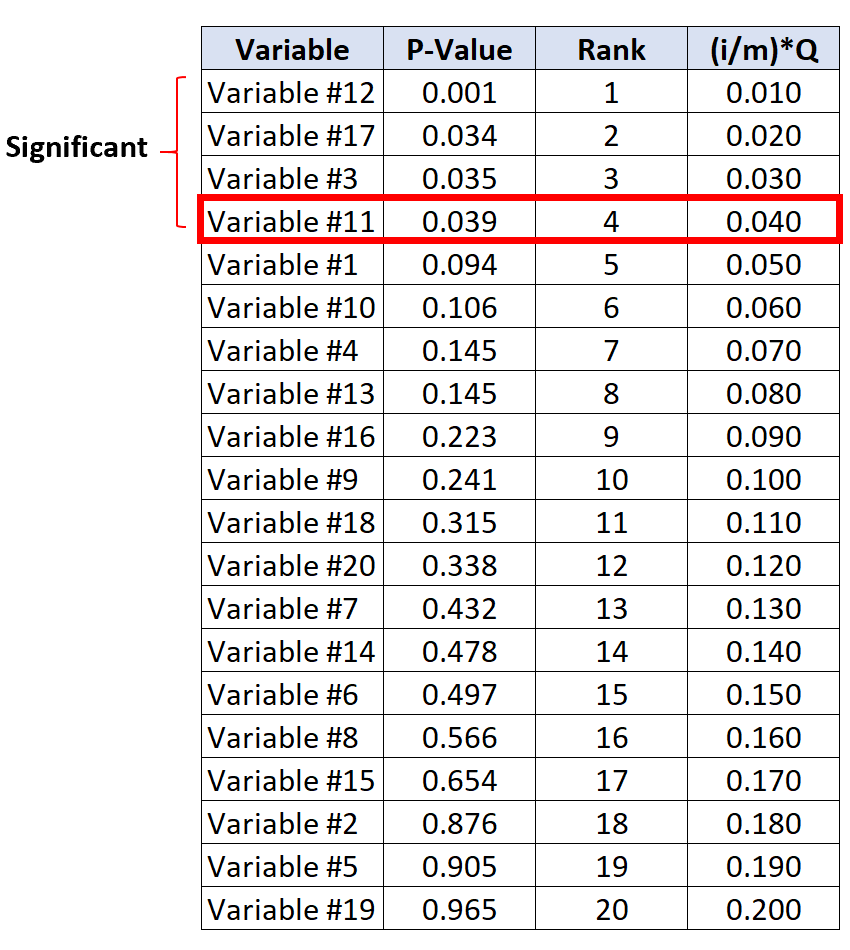
Si noti che anche se le variabili n. 17 e n. 3 non hanno valori p inferiori ai valori critici BH, sono comunque considerate significative perché hanno valori p inferiori rispetto alla variabile n. 11.

Come scegliere un tasso di false scoperte

Uno dei passaggi più importanti nella procedura Benjamini-Hochberg è la scelta del tasso di false scoperte. Dovresti scegliere il tasso di false scoperte prima di raccogliere dati o eseguire test statistici.

In genere, durante la fase esplorativa dell’analisi eseguirai un gran numero di test statistici, a cui faranno seguito altri test per esplorare ulteriormente i risultati.

Se i test di follow-up sono poco costosi, potresti prendere in considerazione l’impostazione di un tasso di false scoperte più elevato, perché anche se hai alcune false scoperte, probabilmente le scoprirai nei test successivi.

Inoltre, se il costo di perdere una scoperta importante è elevato, potresti voler aumentare il tasso di false scoperte in modo da non perdere nulla di importante.

A seconda dei costi della ricerca e dell’importanza di non perdere nessun risultato importante, il tasso di false scoperte varierà da situazione a situazione.

Risorse addizionali

Una spiegazione dei valori P e della significatività statistica
Qual è il tasso di errore per famiglia?